Podręcznik

Metody prognozowania zapotrzebowania 24-godzinnego na energię elektryczną stanowią ważny czynnik poprawy efektywności gospodarowania energią, gdyż umożliwiają precyzyjne planowanie w tej dziedzinie gospodarki. Z tego powodu tematyka ta jest rozwijana na świecie od wielu lat. Stosować można różne metody prognozowania, poczynając od metod liniowych, takich jak algorytmy autoregresyjne (ARX, ARMAX, ARIMA), poprzez różnego rodzaju dekompozycje (Fouriera, SVD, PCA, falkowa), klasyczne metody optymalizacyjne, w tym optymalizacji globalnej (algorytmy genetyczne, ewolucyjne, symulowanego wyżarzania) aż po najczęściej dziś stosowane sztuczne sieci neuronowe [11,24,32,47,48,].

Zwykle próbuje się różnych metod wybierając spośród nich tę, która zapewnia najlepsze działanie systemu prognostycznego na danych weryfikujących, nie biorących udziału w uczeniu. Należy podkreślić, że prognozowanie obciążeń 24-godzinnych należy do zadań trudnych, gdyż obserwuje się dużą zmienność w przebiegu godzinnym obciążeń. Na rys. 14.1 przedstawiono typowy wykres obciążeń godzinnych występujący w Polskim Systemie Elektroenergetycznym (PSE) w jednym roku (8670 godzin).

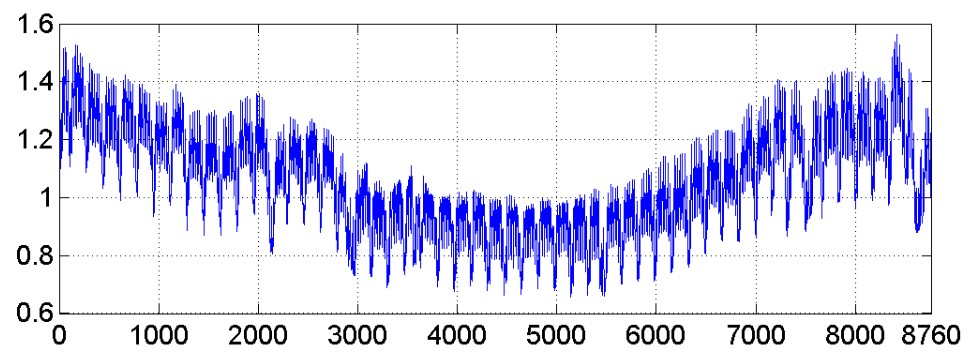
Widoczne jest wyraźne zróżnicowanie obciążeń odpowiadającym różnym godzinom, typom dnia, jak również porze roku. Miesiące zimowe (początek i koniec wykresu) charakteryzują się znacznie większym zapotrzebowaniem na energię, podczas gdy w miesiącach letnich zapotrzebowanie to spada. Widać to wyraźnie na przykładowych danych jednorocznych pokazanych dla małego systemu elektroenergetycznego w tabeli 14.1.

Tabela 14.1 Typowe wartości średniej i odchylenia standardowego odpowiadające różnym porom roku (wartości w MW dla małego systemu elektroenergetycznego

Obciążenie średnie zimą jest najwyższe, przy stosunkowo małej wartości odchylenia standardowego. Obserwując obciążenia poszczególnych dni tygodnia można również zauważyć istotne różnice dla poszczególnych dni, co uwidoczniono w postaci statystyki w tabeli 14.2. Wyraźnie widoczne jest zmniejszenie zapotrzebowania na energię elektryczna w dni świąteczne i weekendy, w stosunku do dni roboczych.

Tabela 14.2 Typowe wartości statystyki odpowiadające różnym dniom tygodnia (wartości w MW dla małego systemu elektroenergetycznego)

Skala powtarzalności predykcji dla poszczególnych dni tygodnia jest odzwierciedlona poprzez stosunek wartości standardowego odchylenia względem wartości średnich (powyżej 20%). Przy takiej skali zmienności obciążeń prognoza naiwna przenosząca wzorzec obciążenia godzinnego doby z jednego tygodnia na drugi generowałaby zbyt duże błędy. Sytuację tę dobrze ilustrują również zależności korelacyjne między poszczególnymi dniami tygodnia. W tabeli 14.3 przedstawiono typowe wartości współczynnika korelacji dla danych małego systemu elektroenergetycznego i jednego roku.

Tabela 14.3 Typowe wartości współczynnika korelacji między poszczególnymi dniami tygodnia

Dni weekendowe są słabiej skorelowane z dniami roboczymi, natomiast dużo lepiej skorelowane są ze sobą. Podobnie dobra korelacja występuje między samymi dniami roboczymi (wartości powyżej 0.93)

W tym wykładzie przedstawimy specjalne podejście do prognozowania, bazujące na zastosowaniu wielu układów prognostycznych na raz. Każdy system prognozy działa na tych samych danych wejściowych. Wyniki działania każdego z nich mogą być integrowane w jednym wspólnym zespole sieci. Takie rozwiązanie pozwala wykorzystać dobre cechy każdego predyktora, pozwalając w ten sposób na uzyskanie precyzyjniejszej prognozy. Pokażemy kilka podejść do integracji wyników działania wielu predyktorów. Wyniki badań teoretycznych zostaną przetestowane na danych rzeczywistych dotyczących Polskiego Systemu Elektroenergetycznego (PSE).