Podręcznik Grafika komputerowa i wizualizacja

Modelowanie nierówności powierzchni jest przykładem tekstury dwuwymiarowej. Metoda ta (ang. bump mapping) została zaproponowana przez Blinna w 1978 roku. Pozwala uzyskiwać widok powierzchni o zmodyfikowanym kształcie bez modyfikowania samej geometrii powierzchni – rysunek 14.7.

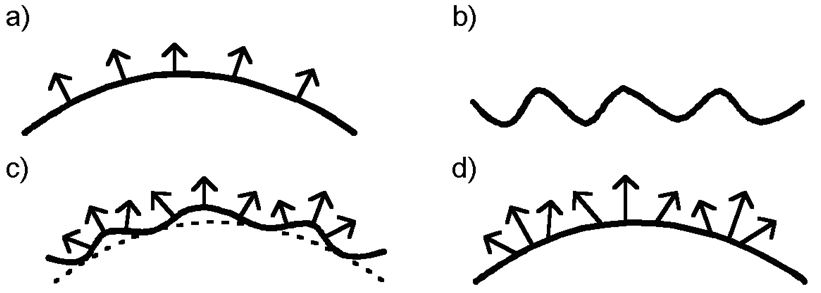
Rys.14.7. Powstawanie  tekstury  Blinna: a) powierzchnia i jej wektory normalne,
b) zaburzenie, c) zaburzenie powierzchni i jej wektory  normalne,
d) zmodyfikowane wektory normalne  odniesione do powierzchni pierwotnej.

Przy zastosowaniu tekstury Blinna zmianę kierunku wektora normalnego uzyskuje się poprzez dodatkową funkcje zaburzenia. Zmodyfikowany wektor normalny jest wykorzystywany w modelu oświetlenia, dzięki czemu są postrzegane lokalne zmiany oświetlenia. Oczywiście wektor zmieniony funkcją zaburzenia może, tak naprawdę, tworzyć dowolny kąt z powierzchnią obiektu, w związku z tym głównym problemem jest dobranie funkcji zaburzenia w taki sposób, aby zmiana wektora odpowiadała rzeczywistej zmianie kształtu powierzchni..

 

Niech   opisuje parametrycznie powierzchnię, która będzie odkształcona. Analogicznie niech  opisuje zaburzenie (teksturę). Wektor normalny   do powierzchni   można wyznaczyć jako:

Jeśli nałożymy teksturę na powierzchnię to powstanie powierzchnia zniekształcona:

Blinn założył, że powstające zaburzenie jest niewielkie, a następnie analizując położenia odpowiednich wektorów wykazał, że aproksymowany wektor normalny do zniekształconej powierzchni można opisać jako

 .

 Przy czym   jest wektorem zaburzenia:

gdzie  i     są wektorami stycznymi do powierzchni    .

 

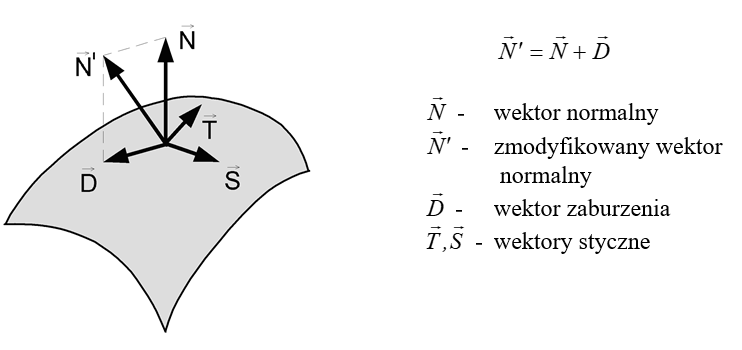
Rys.14.8. Modyfikacja wektora normalnego w mapowaniu Blinna.

Takie rozwiązanie daje bardzo prostą możliwość definicji wektora normalnego odkształconej powierzchni za pomocą wektorów zaburzenia. Wadą zaproponowanej przez Blinna metody jest aproksymacja wektora normalnego. Stąd powstało wiele różnych realizacji tej metody, wykorzystujących różne warianty uproszczenia. Znane są również próby aplikacji sprzętowych mapowania nierówności Blinna.

Rys.14.9. Przykłady zmiany kształtu (wrażenia) za pomocą mapowania nierówności.
a) W sposób uporządkowany. b) W sposób losowy.

Przykłady na rysunku 14.9 pokazują nałożenie tekstury Blinna (mapowania nierówności) na sferę. Warto zwrócić uwagę na linię brzegową rzutu sfery w obu przypadkach. Jest ona okręgiem, niezniekształconym (!). Mapowanie nierówności pozwala uzyskać wrażenie zmian krzywizny bez zmiany geometrii powierzchni. Możliwość niezależnego modelowania kształtu obiektu i drobnych zaburzeń powierzchni jest jedną z podstawowych zalet mapowania nierówności.