Podręcznik

Funkcja charakterystyczna i funkcja przynależności.

Funkcja charakterystyczna:

\( \varphi_A: \mathbb{X} \mapsto \{0,1\} \)

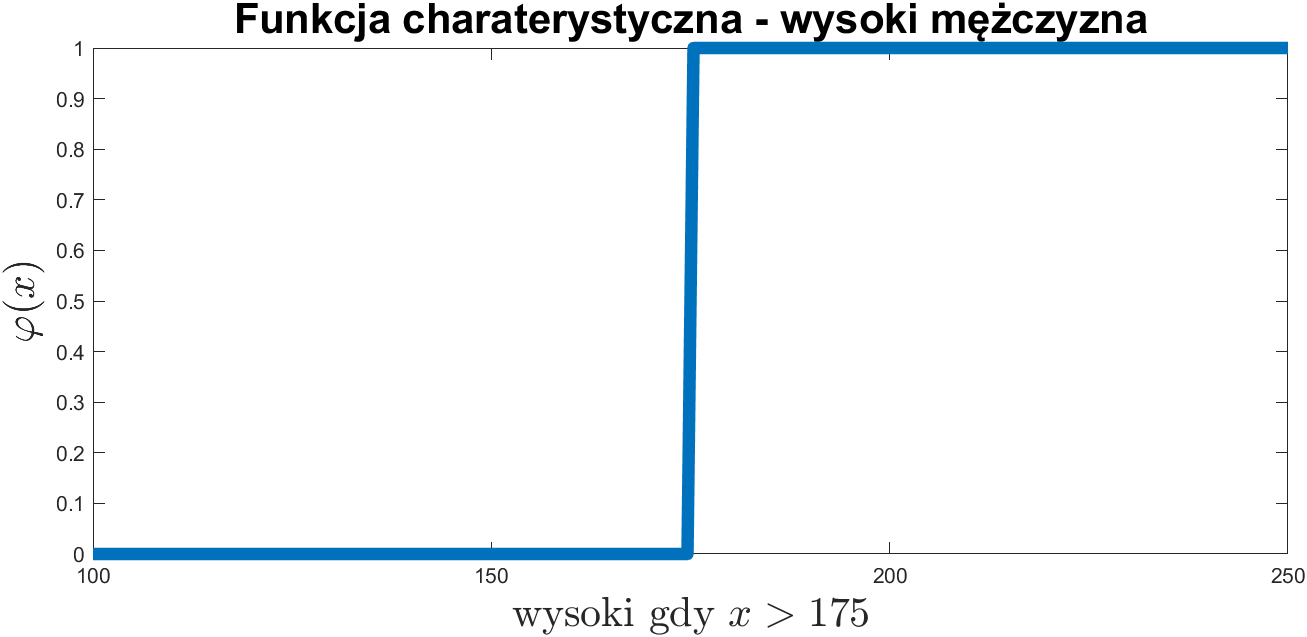
Funkcja  przynależności:

\( \mu_A: \mathbb{X} \mapsto [0,1] \)

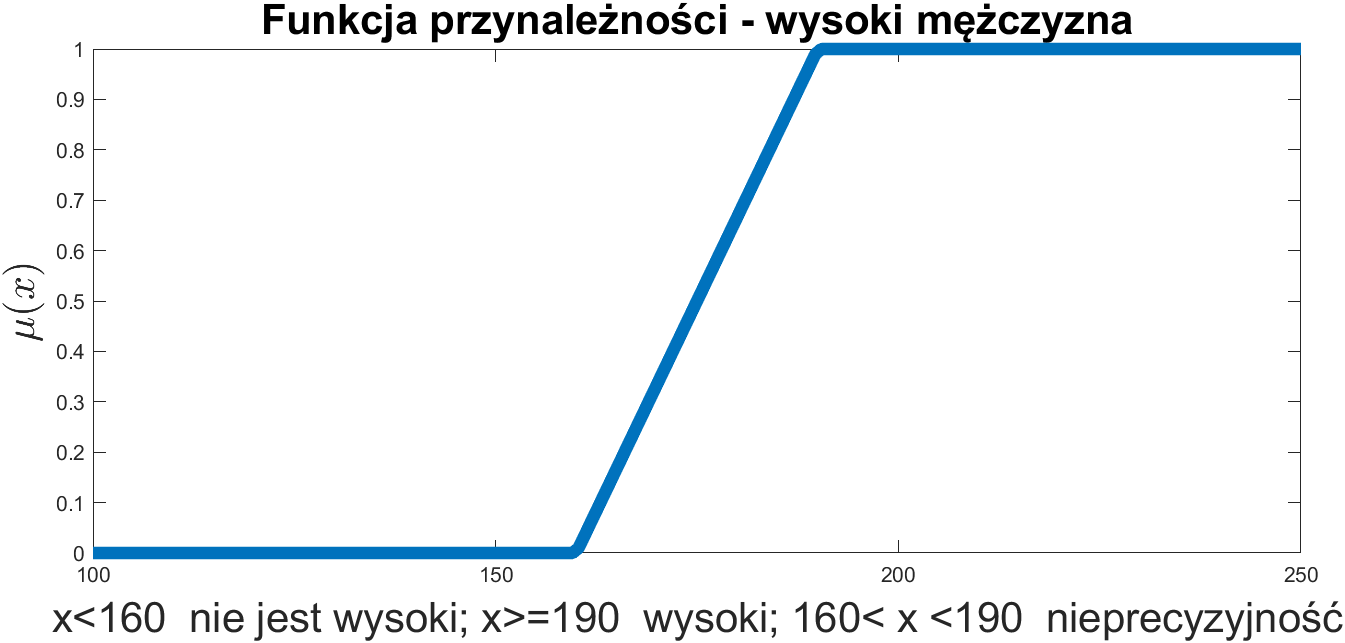
\( \mu _A(x) \) wyraża stopień przynależności  \( x \in \mathbb{X}  \) do zbioru rozmytego A:

• \( \mu _A(x)  = 0\) oznacza, że x nie należy do zbioru A
• \( \mu _A(x)  = 1\) oznacza, że x  należy do zbioru 
• \( \mu _A(x)  \in (0,1) \) oznacza stopień przynależności do zbioru A