Podręcznik

W sieciach przepływowych formułuje się problemy typowe dla sieci przepływowych, w szczególności problem maksymalnego przepływu i problem przepływu minimalnokosztowego. Cała sztuka modelowania polega na „zakodowaniu” problemu, który chcemy rozwiązać w pojęciach ze świata sieci przepływowych. Najpierw dokonujemy więc pewnego mapowania problemu do problemu w sieci przepływowej. Następnie rozwiązujemy odpowiedni problem w sieci przepływowej. Uzyskany w ten sposób wynik dekodujemy z przestrzeni pojęć sieci przepływowej do domeny wyjściowego problemu. Dlatego istotne jest jednoznaczne i poprawne określenie parametrów sieci przepływowej, zazwyczaj przepustowości i kosztów łuków, oraz wskazanie problemu do rozwiązania na sieci. Przedstawimy teraz dwa kluczowe problemy rozwiązywane w sieciach przepływowych.

Problem maksymalnego przepływu

Problem polega na znalezieniu maksymalnego przepływu od wierzchołka źródłowego \(s\) do wierzchołka ujściowego \(t\). W problemie tym muszą zostać zdefiniowane przepustowości krawędzi, natomiast nie są wykorzystywane koszty. 

Poniżej znajduje się przykładowa sieć przesyłowa dla problemu maksymalnego przepływu.

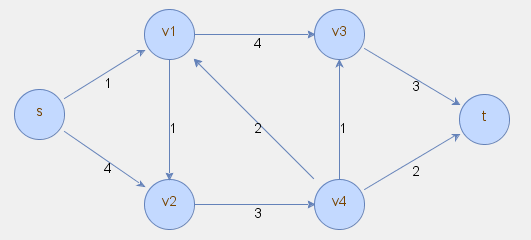
Rozwiązanie problemu maksymalnego przepływu zostało zaznaczone poniżej w postaci przepływów podanych w nawiasach kwadratowych.

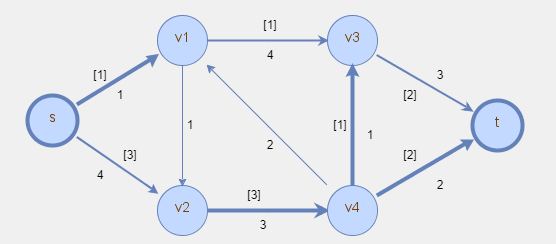
Problem maksymalnego przepływu można rozwiązywać np. algorytmem Forda-Fulkersona. Dla całkowitoliczbowych przepustowości algorytm ten znajduje rozwiązanie całkowitoliczbowe w skończonej liczbie iteracji. Ponieważ w niniejszym materiale skupiamy się na modelowaniu, czytelnika chcącego poznać szczegóły algorytmu odsyłamy do pozycji bibliograficznych.

Model programowania liniowego dla problemu maksymalnego przepływu jest następujący:

\(\max F\)

\(\sum_{v \in V} f_{sv} -F =0\)

\(\sum_{u\in V} f_{vu} - \sum_{u\in V} f_{uv} = 0 \quad v \in V, v \ne s, v \ne t\)

\( 0 \leq f_{uv} \leq c_{uv} \quad (u,v) \in E\)

Z maksymalnym przepływem wiąże się pojęcie minimalnego przekroju.

Przekrojem grafu \(G=(V,E)\) nazywamy podział łuków na dwa rozłączne podzbiory \(S\) oraz \(T= V \setminus S\). Przepustowość przekroju \((S,T)\) to suma przepustowości wszystkich łuków łączących wierzchołki \(s \in S\) z wierzchołkami \(t \in T\).

Wartość dowolnego przepływu w sieci nie może być większa niż przepustowość dowolnego przekroju. W szczególności wartość maksymalnego przepływu w sieci \(G\) jest równa przepustowości minimalnego przekroju w sieci \(G\).

Minimalny przekrój może być wyznaczony np. w ramach ostatniej iteracji algorytmu Forda-Fulkersona, w której finalne znakowanie wierzchołków wyznacza ich podział na podzbiory \(S\) i  \(T\).

Problem najtańszego przepływu

Problem najtańszego przepływu wymaga zdefiniowania jednostkowych kosztów przepływ na łukach. Należy znaleźć przepływ o zadanej wielkości z węzła źródłowego \(s\) do ujścia \(t\) przy minimalnym sumarycznym koszcie przepływu.

Poniżej znajduje się przykładowa sieć przesyłowa dla problemu najtańszego przepływu, gdzie pierwsza liczba z pary x/y oznacza przepustowość, a druga koszt.

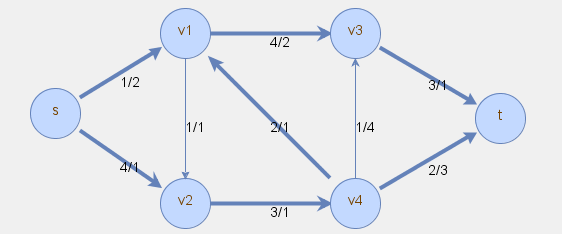
Rozwiązanie problemu najtańszego przepływu zostało zaznaczone poniżej w postaci przepływów podanych w nawiasach kwadratowych.

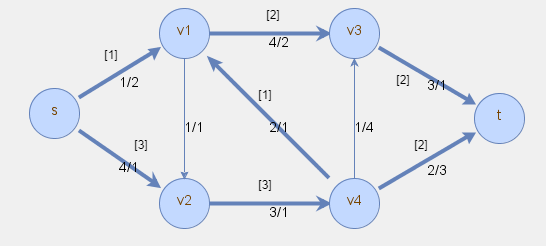
Problem najtańszego przepływu może być rozwiązywany uproszczoną metodą sympleks lub dedykowanymi algorytmami sieciowymi.

Model programowania liniowego dla problemu minimalnokosztowego przepływu \(F\) jest następujący:

\( \min \sum_{(u,v) \in E} \theta_{uv} f_{uv}\)

\( \sum_{v \in V} f_{sv} = F\)

\(\sum_{u\in V} f_{vu} - \sum_{u\in V} f_{uv} = 0 \quad v \in V, v \ne s, v \ne t\)

\( 0 \leq f_{uv} \leq c_{uv} \quad (u,v) \in E\)