Podręcznik

Algorytm Floyda-Warshalla to klasyczna metoda znajdowania najkrótszych ścieżek między wszystkimi parami wierzchołków w grafie. Działa zarówno dla grafów skierowanych, jak i nieskierowanych, pod warunkiem że nie zawierają ujemnych cykli. W przeciwieństwie do algorytmu Dijkstry, który oblicza odległości z jednego źródła, algorytm Floyda-Warshalla działa na całościowym podejściu macierzowym. Rozwiązanie problemu jest również zapisywane w postaci tablicy dwuwymiarowej D o wymiarach n x n gdzie n jest liczbą wierzchołków grafu. W rezultacie wykonania algorytmu w każdej komórce D[i,j] znajduje się wartość odpowiadająca kosztowi najkrótszej ścieżki prowadzącej z wierzchołka i do wierzchołka j, co widać poniżej.

Oprócz samego kosztu najkrótszej drogi prowadzącej między dwoma wierzchołkami, równie cenna jest informacja o przebiegu takiej ścieżki (czyli przez jakie pośrednie wierzchołki przechodzi ta droga). W tym celu równolegle do wyznaczania kosztów ścieżek w tablicy D, wyznaczane są indeksy poprzedników (węzłów poprzedzających inne węzły) znajdujących się na najkrótszych ścieżkach prowadzących do konkretnych węzłów. Jest to zapisywane, i w trakcie działania algorytmu sukcesywnie aktualizowana jest tablica zawierająca indeksy poprzedników (również o rozmiarze n x n), która oznaczymy jako P i szczegółowo omówimy później na przykładzie.

Wartościową zaletą algorytmu Floyda-Warshalla jest fakt, że może być on stosowany dla grafów o ujemnych wagach (w przeciwieństwie do algorytmu Dijkstry wyznaczającego najkrótsze ścieżki z jednego węzła źródłowego – dowiecie się o nim w następnym podrozdziale). Omawiany algorytm jest przykładem metody stosującej zasady programowania dynamicznego. Niebawem w skrócony sposób wyjaśnimy, dlaczego tak właśnie jest.

Na razie spróbujemy Wam przedstawić w sposób możliwie prosty i zwięzły sposób główną ideę algorytmu. Należy przyjąć, że zgodnie z macierzą sąsiedztwa węzły grafu są oznaczone indeksami od 1 do n. Początkowo elementy tablicy D są równe odpowiadającym im elementom macierzy sąsiedztwa T (wystarczy proste przepisanie wartości). Należy pamiętać, że macierz sąsiedztwa T jest konstruowana w taki sposób, że:

• T[i,j] jest równa wadze krawędzi łączącej węzły i, j, jeśli w grafie jest taka krawędź
• T[i, j] = 0, jeśli i=j
• T[i,j]= +Inf, jeżeli nie istnieje krawędź łącząca wierzchołki i, j

A zatem we wstępnej fazie algorytmu najkrótsze ścieżki między dowolną parą węzłów posiadają koszt równy wadze krawędzi łączącej te dwa wierzchołki (jeśli takowa istnieje - najkrótsza ścieżka nie może zawierać w tym momencie żadnych węzłów pośrednich). W kolejnych krokach algorytm rozpatruje kolejno węzły oznaczone indeksem 1,2,....,k,....,n. Najpierw sprawdzane jest (dla każdej pary węzłów i, j), czy ścieżka z i do j prowadząca przez pośredni węzeł o indeksie 1 jest krótsza niż aktualnie znana najkrótsza droga między wierzchołkami i oraz j (bez żadnych węzłów pośrednich). Jeśli tak właśnie jest, to długość najkrótszej ścieżki jest aktualizowana (wiedzie ona teraz przez węzeł 1). W kolejnym kroku algorytm sprawdza, czy włączenie węzła 2 do najkrótszej ścieżki z i do j nie poprawi wartości jej długości. Wówczas wartość D[i,j] będzie zawierać długość najkrótszej ścieżki prowadzącej bezpośrednio z węzła i do j lub też zawierającej co najwyżej węzły 1 oraz 2 jako wierzchołki pośrednie. W ogólności, po k-tym kroku, zostaną obliczone najkrótsze ścieżki między parami wierzchołków, zawierające węzły pośrednie ze zbioru wierzchołków o indeksach (1,..,k). Tym samym po zakończeniu działania algorytmu w tablicy D będą wyliczone koszty najkrótszych ścieżek, które mogą przebiegać przez wszystkie węzły grafu G – w tym momencie otrzymywane jest ostateczne rozwiązanie problemu znalezienia najkrótszych ścieżek miedzy parami wierzchołków grafu.

Procedurę możemy przedstawić za pomocą następującego pseudokodu:

skopiuj wartości macierzy sąsiedztwa T do tablicy D
	inicjalizuj tablicę P zerami

	for (każdy węzeł k grafu spośród węzłów (1,..,n) )
		for (każdy węzeł i grafu spośród węzłów (1,..,n) )
			for (każdy węzeł j grafu spośród węzłów (1,..,n) )
				if (D[i,k]+D[k,j] < D[i,j])	{
					D[i,j] = D[i,k] + D[k,j] 	//najkrótsza ścieżka prowadzi teraz przez węzeł k
					P[i,j] = k
				}

Poniżej przedstawiony jest przykład graficzny działania algorytmu Floyda-Warshalla.



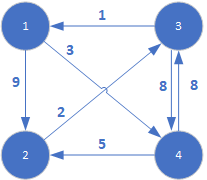
Wartość 999 w komórkach tablicy D jest odpowiednikiem +Inf, natomiast wartość 0 w tablicy P oznacza, że na ścieżce między wierzchołkiem początkowym a końcowym nie ma ani jednego wierzchołka pośredniego (0 jest praktycznym zapisem wartości NULL). 

Rozpoczynamy właściwy, pierwszy krok nadrzędnej pętli. Sprawdzamy, czy wstawienie wierzchołka k=1 poprawi wartości najkrótszych ścieżek między wierzchołkami grafu:

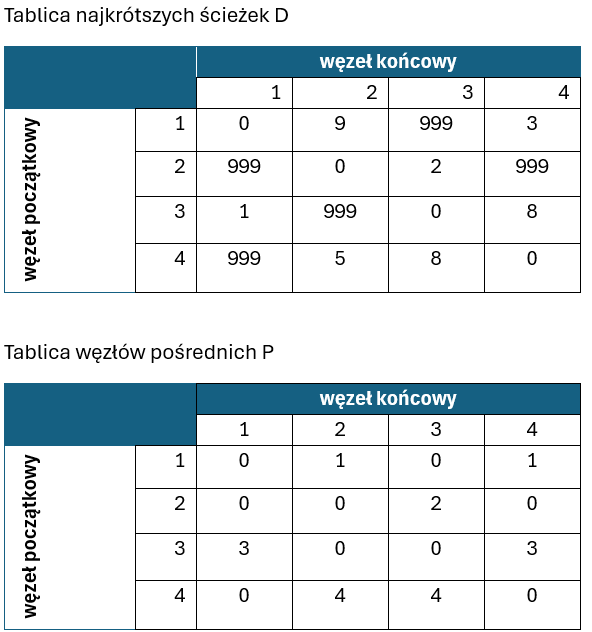
Okazuje się, że zastosowanie węzła 1 jako wierzchołka pośredniego poprawia długość najkrótszej ścieżki między węzłami 3->2 oraz 3->4. Zmiany wartości najkrótszych ścieżek zaznaczono pomalowaniem odpowiednich komórek tablicy T. W związku z dodaniem nowego węzła pośredniego do ścieżek, w odpowiednie miejsca w tablicy P wstawiana jest wartość indeksu węzła 1.

Przechodzimy do drugiego kroku iteracji. W tym momencie próbujemy poprawić najkrótsze ścieżki przy użyciu węzła o indeksie k=2:

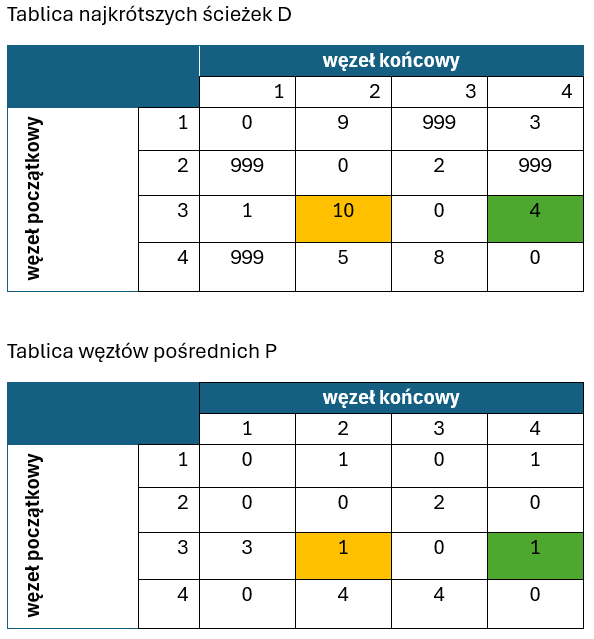
W tym kroku algorytm poprawia dwie ścieżki poprzez umieszczenie w nich węzła 2. Mianowicie dotyczy to:

• drogi 1->3, gdyż T[1,2]+T[2,3] = 9 +2 = 11 i jest mniejsze niż T[1,3]= 999 (oczywiście mamy na myśli dotychczasową wartość T[1,3], która właśnie jest modyfikowana)
• drogi 4->3, gdyż T[4,2]+T[2,3] = 5 + 2 = 7 i jest mniejsze niż T[4,3] = 8

Tak jak w poprzedniej iteracji, zmienione wartości najkrótszych ścieżek, a w tablicy P wstawiono dla uaktualnionych ścieżek indeks nowo umieszczonego węzła pośredniego.

Przejdźmy do iteracji o numerze k=3:

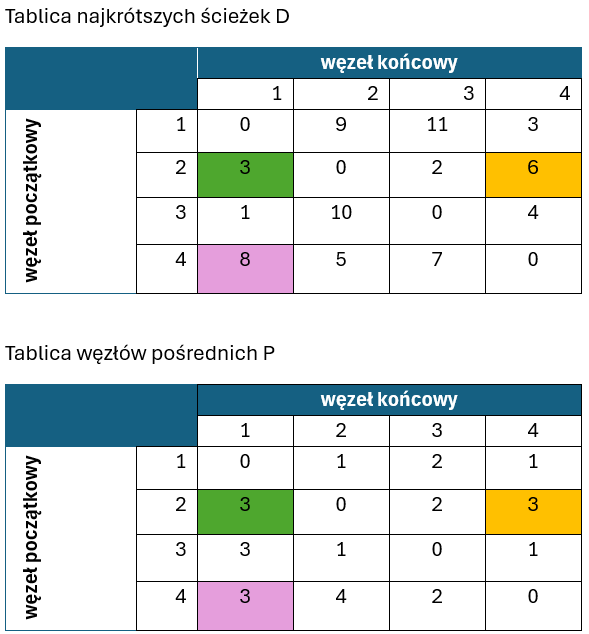
Tym razem aż trzy ścieżki wymagały poprawienia. Są nimi:

• ścieżka 2->1, gdyż T[2,3]+T[3,1] = 2 +1 = 3 i jest mniejsze niż T[2,1]= 999
• ścieżka 2->4, gdyż T[2,3]+T[3,4] = 2 +4 = 6 i jest mniejsze niż T[2,4]= 999
• ścieżka 4->1, gdyż T[4,3]+T[3,1] = 7 +1 = 8 i jest mniejsze niż T[4,1]= 999

W tablicy P w odpowiednich miejscach wstawiamy indeks węzła 3.

Pozostał nam już tylko ostatni, czwarty krok iteracji:

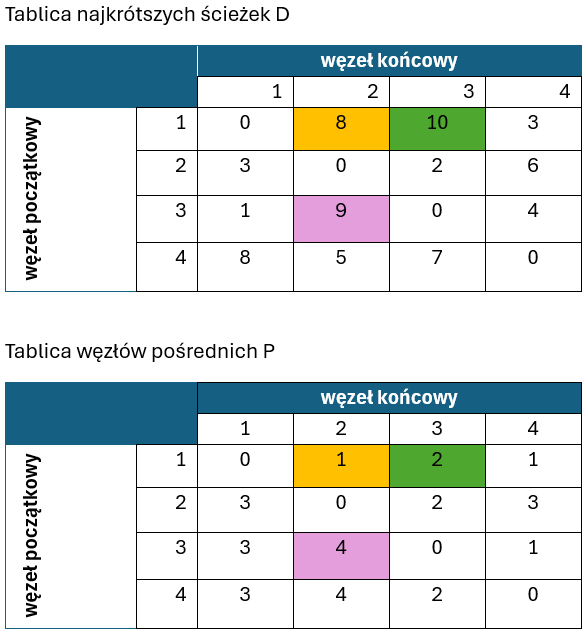
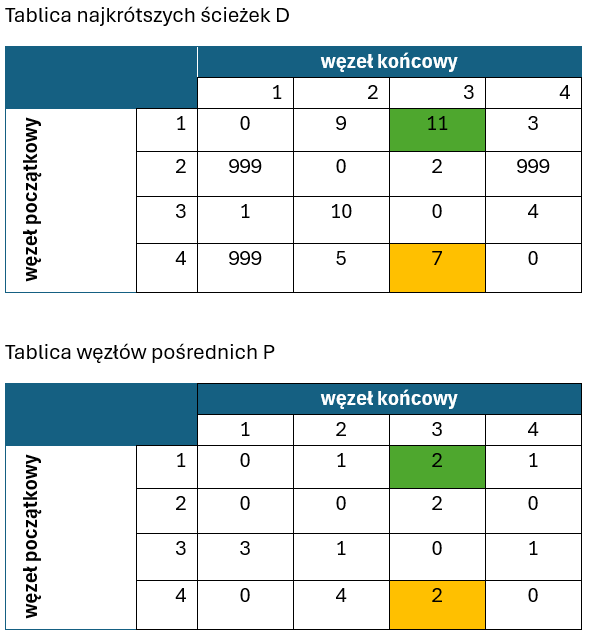
Jak się okazało, ponownie trzy drogi wymagały uaktualnienia – w tym przypadku za pomocą węzła o indeksie 4. Odnosi się to do ścieżek:

• 1->2, gdyż T[1,4]+T[4,2] = 3 +5 = 8 i jest mniejsze niż T[1,2]= 9
• 1->3, gdyż T[1,4]+T[4,3] = 3 +7 = 10 i jest mniejsze niż T[1,3]= 11
• 3->2, gdyż T[3,4]+T[4,2] = 4 +5 = 9 i jest mniejsze niż T[3,2]= 10

Ponieważ sprawdziliśmy już wszystkie cztery węzły w roli wierzchołków pośrednich należących do najkrótszych ścieżek, algorytm Floyda-Warshalla kończy w tym miejscu swój proces. Wszystkie najkrótsze ścieżki między każdą parą węzłów grafu zostały wyznaczone.

Możemy również na podstawie tablicy P odtworzyć przebieg najkrótszej ścieżki: przykładowo chcemy wiedzieć, którędy biegnie najkrótsza droga z węzła 1 do węzła 3. W tym celu celu odczytujemy P[1,3] = 4, następnie sprawdzamy P[1,4] = 1 (czyli ścieżka ta jest pojedynczą krawędzią) oraz P[4,3]= 2. Następnie odczytujemy wartość P[4,2] = 4 oraz P[2,3] = 2, a zatem doszliśmy już do elementarnych części tej ścieżki. Przebiega ona w sposób następujący: 1->4->2->3.