Podręcznik

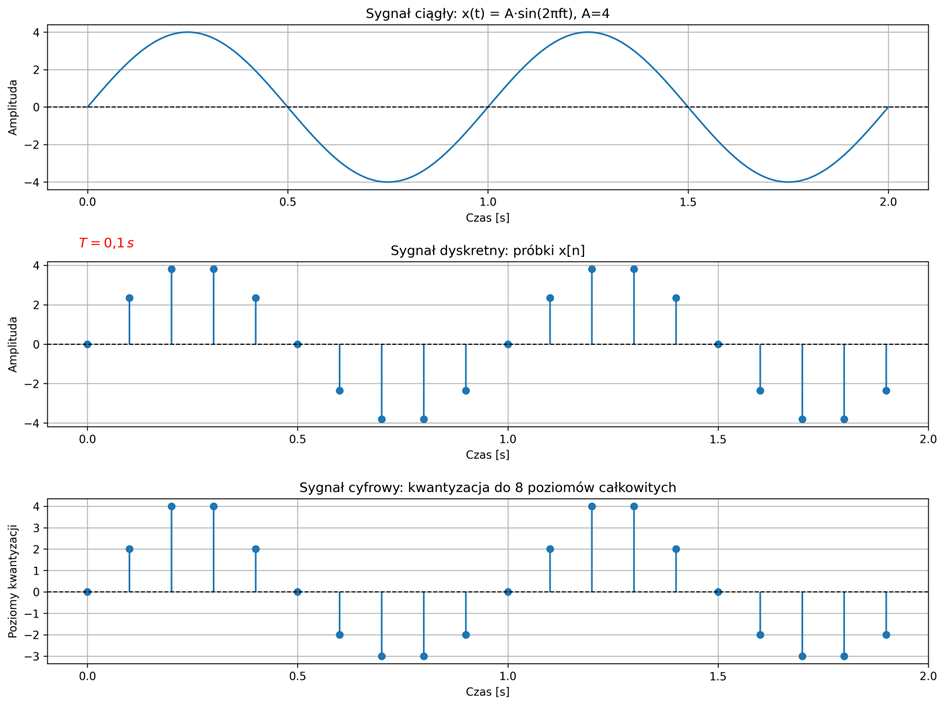
Sygnały są nośnikami informacji, których wartości można zmierzyć i za ich pomocą przekazywana jest informacja. Może ona mieć charakter ciągły, przyjmując nieskończoną liczbę wartości, lub charakter dyskretny, ograniczony do skończonej liczby wartości. Dziedzina i zakres określoności sygnałów informują o tym, jak zmienia się zmienna niezależna opisująca sygnał, na przykład czas lub przestrzeń, oraz jakie wartości może przyjmować sygnał. Stanowią one podstawowe kryterium podziału sygnałów.

Wyróżnia się trzy podstawowe typy sygnałów:

• analogowe,
• dyskretne,
• cyfrowe.

Termin analogowy jest używany przy opisie sygnału, który jest ciągły w czasie i ma ciągły zakres wartości – tzw. ciągły w amplitudzie. W przypadku sygnału dyskretnego, jego wartości określone są tylko w wybranych chwilach czasowych, a amplitudy próbek sygnału należą do zbioru liczb rzeczywistych. Sygnał cyfrowy to sygnał o czasie dyskretnym, którego zbiór wartości również jest dyskretny – tzw. dyskretny w amplitudzie. Sygnały cyfrowe są sygnałami dyskretnymi, dla których przeprowadzono operację kwantowania – przypisywania każdej wartości próbki do najbliższej wartości z ograniczonego zbioru możliwych poziomów. Komputery i systemy cyfrowe nie mogą zapisywać nieskończonej liczby wartości, dlatego dyskretyzacja sygnału w amplitudzie pozwala przetwarzać i przechowywać dane w formie cyfrowej.

W dalszej części rozważań analizowane będą wyłącznie sygnały ciągłe w czasie oraz ich próbkowe wersje dyskretne. Procesy kwantyzacji i kodowania, które są etapami przekształcania sygnału do postaci cyfrowej, nie będą tutaj uwzględniane. Zwykle są one realizowane automatycznie przez przetworniki analogowo-cyfrowe i systemy komputerowe, dlatego nie wpływają na zrozumienie podstawowych problemów związanych z przetwarzaniem sygnałów.

Przyjmijmy formalny zapis jednowymiarowego sygnału jako:

\( x(t) \) lub \( x[n] \)

gdzie:

• \( x(t) \) – sygnał ciągły w czasie \( t \),
• \( x[n] \) – sygnał dyskretny, określony tylko w wybranych chwilach czasowych \( n\in D \).

Zbiór \( D \) wartości zmiennej dyskretnej \( n \) jest zwykle zbiorem wszystkich liczb całkowitych, zbiorem liczb naturalnych lub jego skończonym podzbiorem \( [n_1, n_2] \).

Dziedziną sygnałów ciągłych \( x(t) \) może być:

• zbiór liczb \( \mathbb{R} \) – w modelach matematycznych,
• dodatnia półoś \( [0,\infty) \) – w modelach przyczynowych,
• odcinek \( [t_1, t_2] \) osi czasu – fizycznie istniejące układy.

W przypadku sygnałów dyskretnych \( x[n] \), dziedziną jest zwykle zbiór chwil \( t_n = nT \), \( n\in \mathbf{D} \), odległych od siebie o stały odstęp \( T \), nazywany okresem próbkowania lub przedziałem dyskretyzacji. Istotny dla nas będzie jedynie kolejny numer w ciągu próbek, a nie w jakiej chwili \( t_n \) została pobrana próbka. Dlatego też, argumentem sygnału dyskretnego będzie czas unormowany względem okresu próbkowania, czyli \( n = t_n/T \).

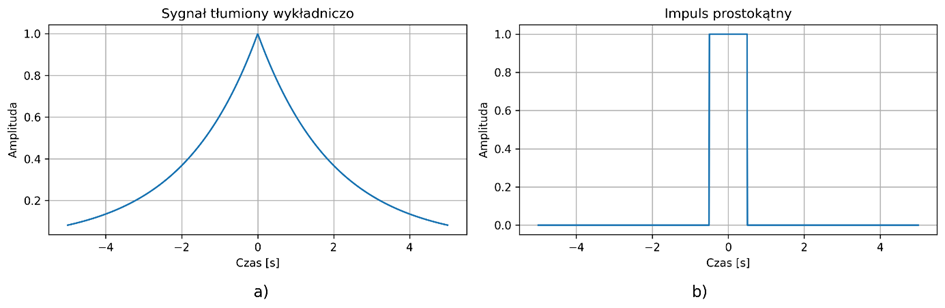
Jeżeli sygnał przyjmuje wartości różne od zera:

• w przedziale nieskończonym, to nazywamy go sygnałem o nieskończonym czasie trwania,
• w przedziale skończonym, to nazywamy go sygnałem o skończonym czasie trwania lub sygnałem impulsowym.