Podręcznik
Wymagania zaliczenia
2. Sygnały i ich charakterystyki
2.3. Przekształcenia sygnałów
Przekształcenia sygnałów w dziedzinie czasu to operacje, które zmieniają ich kształt, pozycję lub wartości. Do podstawowych operacji można zaliczyć przesunięcie, skalowanie i odwrócenie w czasie, skalowanie amplitudy, dodanie składowej stałej i odwrócenie amplitudy.
- Przesunięcie w czasie – sygnał \( x(t) \) jest przesuwany o \( t_0 \) w lewo lub prawo na osi czasu (rys. 2.3b-c):
\( y(t)=x(t-t_0) \)
- jeśli \( t_0 < 0 \) to mamy do czynienia z przyśpieszeniem sygnału,
- jeśli \( t_0 > 0 \) to mamy do czynienia z jego opóźnieniem.
- Skalowanie w czasie – zmiana szybkości przebiegu sygnału \( x(t) \) poprzez stały współczynnik skalowania czasu \( a \) (rys. 2.3d):
\( y(t)=x(at) \)
- jeśli \( \lvert a \rvert < 1 \) to mamy do czynienia z „rozciąganiem” sygnału w czasie,
- jeśli \( \lvert a \rvert > 1 \) to mamy do czynienia z jego „ściskaniem” w czasie.
- Odwrócenie w czasie – zmiana kierunku przebiegu czasu poprzez odbicie sygnału \( x(t) \) względem osi pionowej (rys. 2.3e):
\( y(t)=x(-t) \)
- Skalowanie amplitudy – zmiana wartości sygnału \( x(t) \) poprzez stały współczynnik skalowania amplitudy \( A \) (rys. 2.3f):
\( y(t)=A\,x(t) \)
- jeśli \( 0 < A < 1 \) to mamy do czynienia z osłabieniem sygnału – amplituda maleje, zachowując kształt w czasie,
- jeśli \( A > 1 \) to mamy do czynienia ze wzmacnianiem sygnału – amplituda rośnie, jednocześnie zachowując jego kształt w czasie,
- jeśli \( A < 0 \) to mamy do czynienia z operacją odwracania w czasie i skalowania amplitudy.
- Dodanie składowej stałej – przesunięcie sygnału \( x(t) \) w górę lub w dół o stałą wartość \( C \) (rys. 2.3g):
\( y(t)=x(t)+C \)
- jeśli \( C < 0 \) to mamy do czynienia z przesunięciem sygnału o \( C \) jednostek w dół, zachowując jego kształt w czasie,
- jeśli \( C > 0 \) to mamy do czynienia z przesunięciem sygnału o \( C \) jednostek w górę, zachowując jego kształt w czasie.
- Odwrócenie amplitudy – zmiana znaku każdej wartości sygnału na przeciwną poprzez odbicie sygnału \( x(t) \) względem osi poziomej (rys. 2.3h):
\( y(t)=-x(t) \)
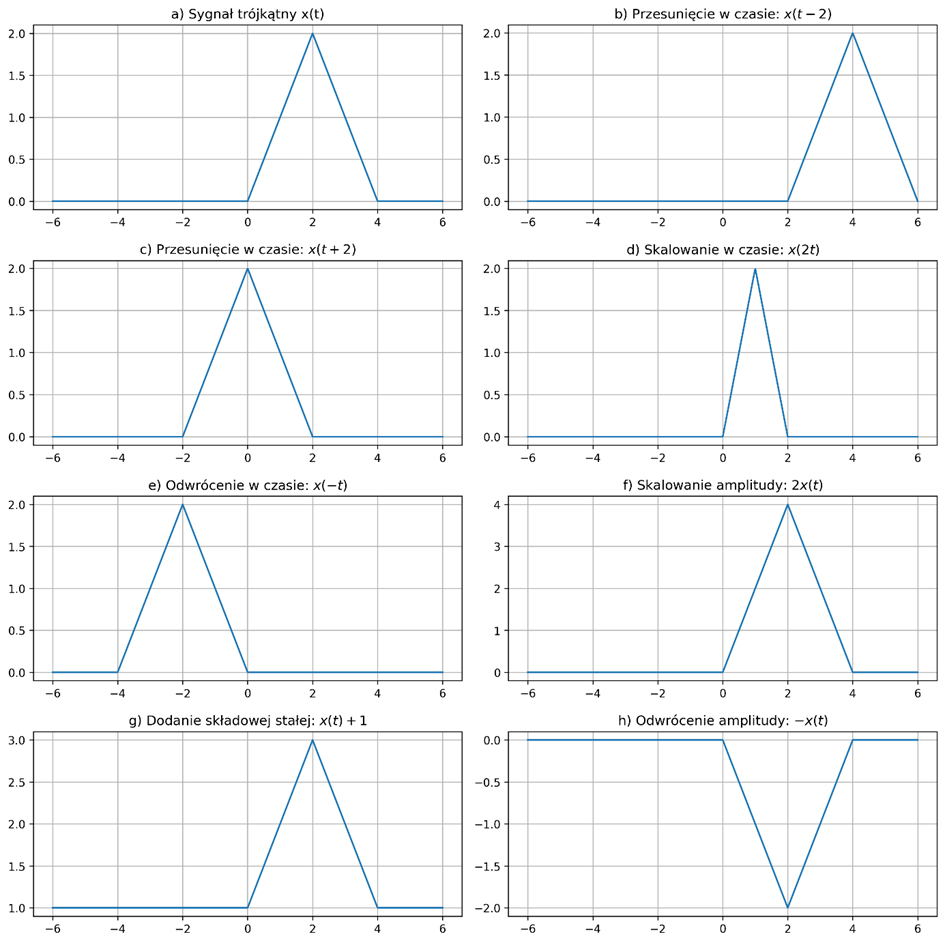
Rys. 2.3. Podstawowe rodzaje przekształceń sygnału trójkątnego
Przesunięcie z odwróceniem sygnału w czasie posłuży nam do obliczania splotu dwóch sygnałów – operacji opisanej w rozdziale 2.4.
