2. Sygnały i ich charakterystyki

2.7. Sygnały zespolone

Oprócz sygnałów rzeczywistych, wykorzystywane są sygnały zespolone, które pomimo abstrakcyjnego charakteru ułatwiają analizę i przetwarzanie – zwłaszcza w dziedzinie częstotliwości. Sygnał zespolony przyjmuje wartości zespolone i ma postać algebraiczną:

z(t) = x(t) + j y(t)

gdzie

  • x(t) = \operatorname{Re}\{z(t)\} i y(t) = \operatorname{Im}\{z(t)\} są sygnałami rzeczywistymi,
  • j jest jednostką urojoną, dla której j^2 = -1

Sygnał zespolony można również przedstawić w postaci wykładniczej:

z(t) = |z(t)| e^{j\varphi(t)}

gdzie

  • |z(t)| = \sqrt{x^2(t)+y^2(t)} jest modułem sygnału,
  • \varphi(t) = \arctan\frac{y(t)}{x(t)} jest argumentem sygnału.

Sygnałem sprzężonym z sygnałem z(t) nazywamy sygnał:

z^{\ast}(t) = x(t) - j y(t) = |z(t)| e^{-j\varphi(t)}

Sygnały zespolone również dzielimy na sygnały o ograniczonej energii i ograniczonej mocy. Wzory na energię i moc sygnałów zespolonych są zdefiniowane identycznie jak w przypadku sygnałów rzeczywistych, z tą różnicą, że w ich sformułowaniach pojawia się moduł |x(t)|^2 zamiast kwadratu sygnału x^2(t) .

Analogiczne są również wzory na funkcję korelacji wzajemnej i funkcję autokorelacji sygnałów zespolonych o ograniczonej energii, z tą różnicą, że w iloczynie skalarnym pojawia się sprzężone zespolone przesunięcie jednego z sygnałów:

R_{xy}(\tau) = \int_{-\infty}^{\infty} x(t)\,y^{\ast}(t-\tau)\,dt

Najbardziej znanymi sygnałami zespolonymi są:

  • zespolony sygnał sinusoidalny:
z(t) = e^{j\omega t} = \cos(\omega t) + j \sin(\omega t), \quad t \in \mathbb{R}
  • sygnał analityczny, który powstaje z rzeczywistego sygnału x(t) :
z_x(t) = x(t) + j \hat{x}(t)

którego częścią rzeczywistą jest sygnał x(t) , a częścią urojoną jest transformata Hilberta sygnału x(t) .

Na rys. 2.14 przedstawiono zespolony sygnał z(t) = e^{j2\pi f t} – przebieg jego części rzeczywistej i urojonej. Podobnie jak dla sygnałów rzeczywistych, można z wykresów odczytać, jak wyglądają oscylacje w dziedzinie czasu, powtarzalność i strukturę fazową, a także oszacować, jaki jest okres. Energia i moc przykładowego sygnału wynosi 1.

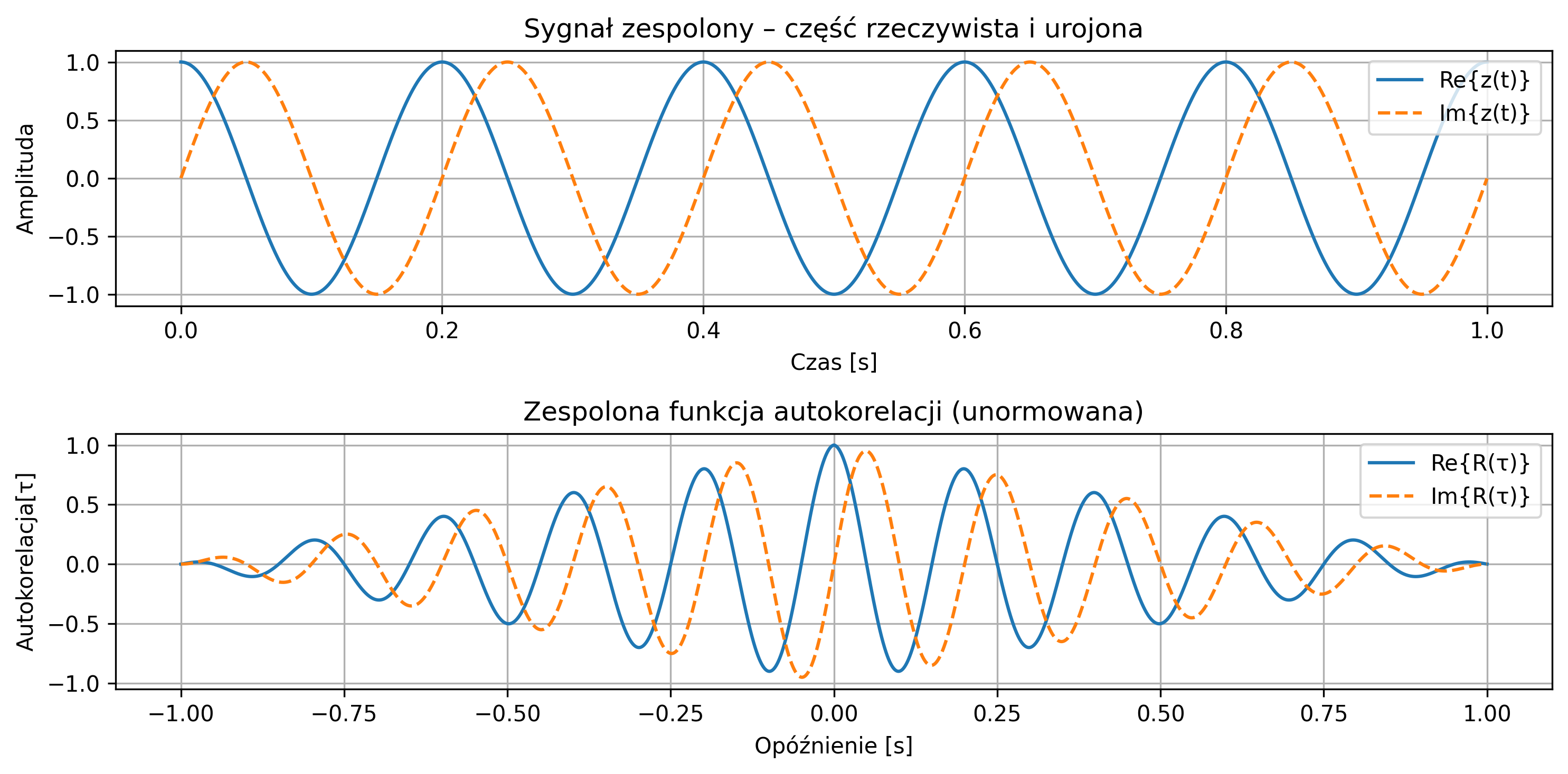
Rys. 2.14. Wykres unormowanej funkcji autokorelacji sygnału zespolonego
 
Sygnały zespolone są szczególnie użyteczne w analizie modulacji, gdy interesuje nas:
  • amplituda chwilowa – moduł sygnału,
  • faza chwilowa – zmiana kąta argumentu,
  • obwiednia sygnału rzeczywistego – sposób, w jaki „kształt” energii sygnału zmienia się w czasie.

Ponadto sygnały zespolone są szeroko stosowane w przetwarzaniu sygnałów biomedycznych, takich jak EKG czy EEG, gdzie analiza fazy i obwiedni jest kluczowa dla diagnozy, na przykład przy wykrywaniu drżeń mięśni, zaburzeń rytmu serca lub analizie związków między regionami mózgu.