Podręcznik

Parametry energetyczne sygnałów to miary opisujące ilość energii zawartej w sygnale lub jego moc w czasie, które pozwalają na ilościową ocenę jego właściwości. W analizie i przetwarzaniu sygnałów mają kluczowe znaczenie, ponieważ umożliwiają:

• ocenę amplitudy i intensywności sygnału,
• wykrywanie zmian i anomalii,
• porównywanie i klasyfikowanie sygnałów,
• dobór parametrów filtrów i algorytmów przetwarzania,
• ocenę jakości sygnału.

W kontekście sygnałów biomedycznych analiza parametrów energetycznych jest niezwykle istotna, ponieważ pozwala na ilościową ocenę zarówno aktywności biologicznej, jak i jakości sygnałów rejestrowanych przez aparaturę medyczną. Energia i moc sygnału umożliwiają m.in.:

• ocenę intensywności procesów fizjologicznych – np. amplituda i energia sygnału EKG odzwierciedlają siłę skurczów serca, energia sygnałów EEG koreluje z poziomem aktywności mózgu, a sygnały EMG odzwierciedlają aktywność mięśni,
• wykrywanie nieprawidłowości i patologii – nagłe zmiany energii sygnału mogą wskazywać na arytmie serca, napady epilepsji, migotanie przedsionków lub inne stany chorobowe,
• ocenę jakości sygnału i skuteczności przetwarzania – sygnały o niskiej energii w stosunku do szumu wymagają wzmocnienia lub filtracji, co jest istotne w telemedycynie i zdalnym monitoringu pacjentów,
• dobór parametrów filtrów i algorytmów analizy – energia sygnału pozwala określić, które składowe częstotliwości są istotne, a które stanowią zakłócenia, co ma znaczenie przy projektowaniu algorytmów do analizy EKG, EEG i EMG,
• porównania między pacjentami lub stanami fizjologicznymi – parametry energetyczne umożliwiają obiektywne porównanie sygnałów w różnych warunkach, np. spoczynkowych, wysiłkowych czy patologicznych.

Sygnały deterministyczne przyjmują w dowolnej chwili czasowej wartości rzeczywiste, które są określone przez jawne zależności matematyczne. Z takimi sygnałami wiąże się wiele parametrów, które charakteryzują ich właściwości. Wartość średnia, energia, moc średnia i wartość skuteczna należą do najważniejszych parametrów sygnałów.

• Wartością średnią ciągłego sygnału \( x(t) \), określonego w przedziale \( [t_1, t_2] \), nazywamy wielkość:

• W przypadku sygnału o nieskończonym czasie trwania, wartością średnią nazywamy wielkość graniczną:

• Energią ciągłego sygnału \( x(t) \) nazywamy wielkość:

• Mocą średnią ciągłego sygnału \( x(t) \) nazywamy wielkość graniczną:

• Mocą średnią ciągłego sygnału \( x(t) \) o skończonym czasie trwania, określonego w przedziale \( [t_1, t_2] \), nazywamy wielkość:

• Wartością skuteczną ciągłego sygnału \( x(t) \) jest nazywany pierwiastek z jego mocy:

Wartości energii i mocy sygnału odnoszą się nie bezpośrednio do fizycznych zjawisk, lecz do analizy właściwości sygnału. W teorii sygnałów często nie przypisuje się jednostki sygnału. W takim przypadku wymiarem energii sygnału jest sekunda, natomiast moc jest bezwymiarowa.

Energia i moc charakteryzują właściwości energetyczne sygnału. Na ich podstawie sygnały deterministyczne (ciągłe lub dyskretne) można podzielić na dwie klasy:

• sygnały o ograniczonej energii, gdy:

• sygnały o ograniczonej mocy, gdy:

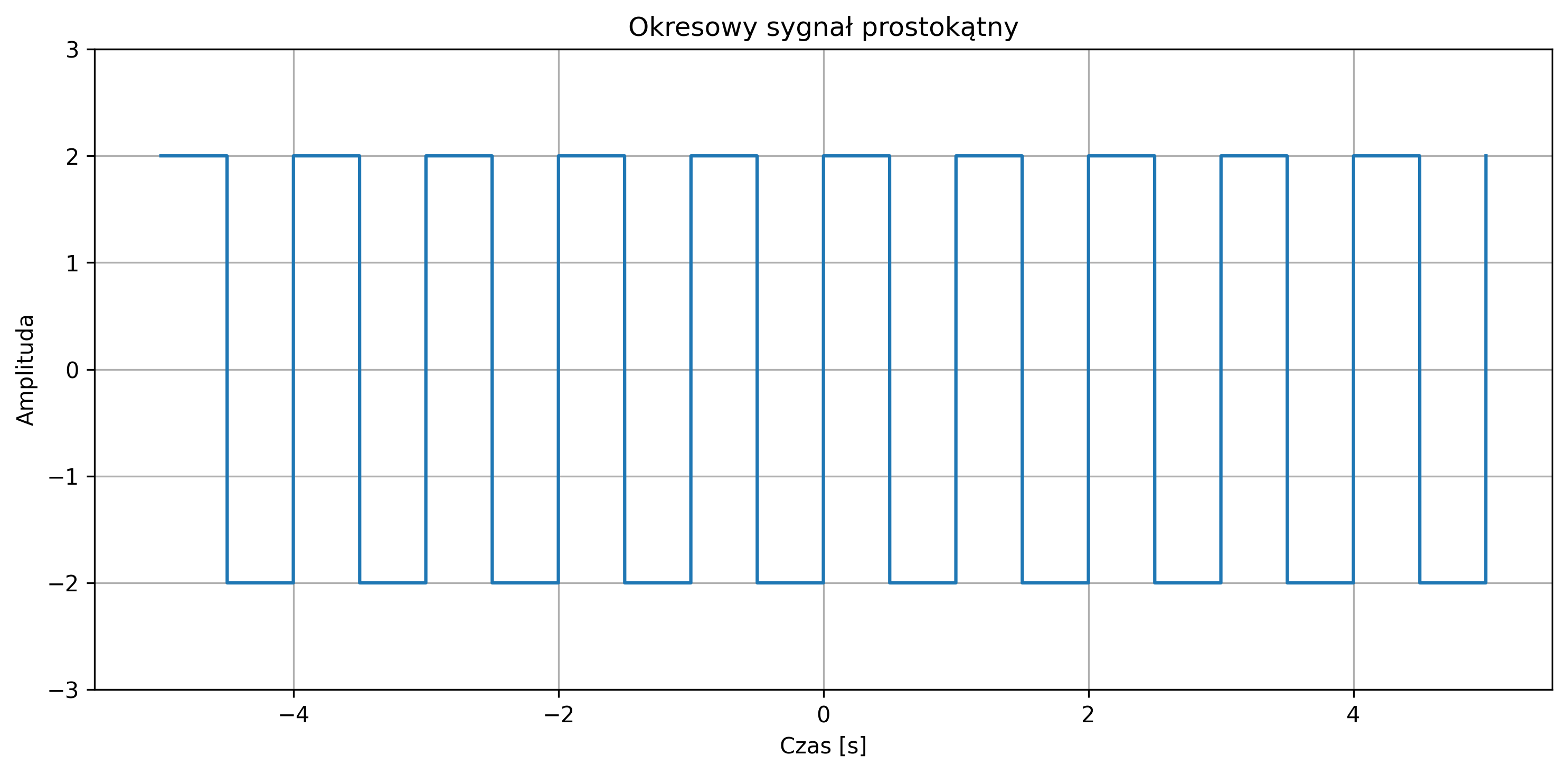
Na rys. 2.8 przedstawiono okresowy sygnał prostokątny o amplitudzie \( A = 2 \), którego moc średnia jest ograniczona i równa \(4\) (\( A^2 \)), zaś jego energia z czasem rośnie do nieskończoności.

Do sygnałów o ograniczonej energii zaliczamy:

• sygnały impulsowe o ograniczonej amplitudzie, np.:
  • impuls prostokątny, trójkątny, radiowy,
  • impulsowy skurcz mięśnia w EMG,
• sygnały o nieskończonym czasie trwania, np.:
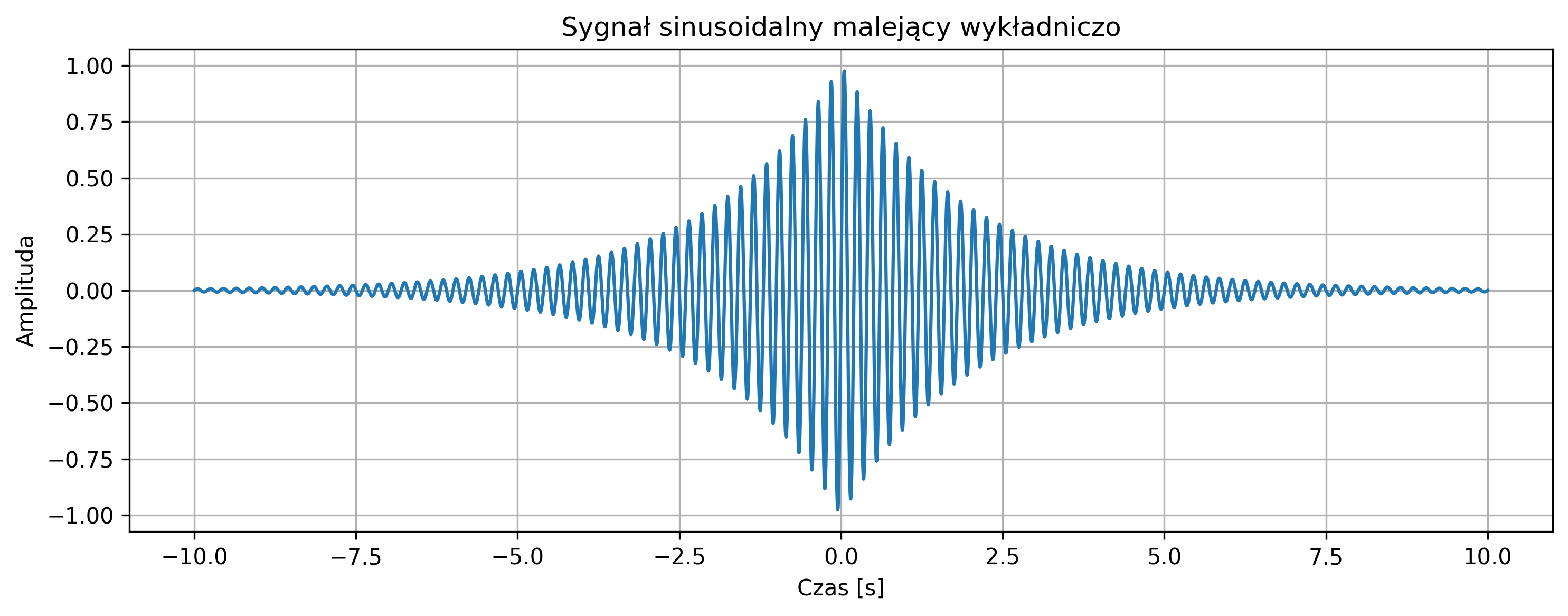
  • sygnał sinusoidalny malejący,
  • sygnał Gaussa,
  • sygnał wykładniczy malejący – odpowiedź tkanek na krótki impuls stymulacji nerwowej w badaniu przewodnictwa (ENG), podczas którego rejestruje się odpowiedź mięśni lub nerwu,
• sygnały nieustalone, np.:
  • drgania tłumione,
  • sygnał EEG z napadem padaczkowym – nieregularny i zmienny, po napadzie zwykle wraca do wartości typowych.

Sygnały o ograniczonej mocy i ograniczone w amplitudzie są sygnałami o nieskończonym czasie trwania:

• sygnały nieokresowe, np.:
  • długotrwały EMG przy skurczu izometrycznym – stała aktywność mięśnia, np. przy utrzymywaniu pozycji,
• sygnały okresowe, np.:
  • sygnał sinusoidalny, fala prostokątna bipolarna,
  • długotrwały sygnał EKG – ciągła rejestracja rytmu serca, np. z użyciem Holtera, sygnał okresowy i stabilny, o regularnym rytmie serca.

Szczególną podklasą sygnałów o ograniczonej mocy są sygnały okresowe. Sygnał opisany funkcją okresową czasu nazywamy sygnałem okresowym. Dla sygnału okresowego \( x(t) \) istnieje taka wartość \( T \), dla której spełniony jest warunek:

dla każdego \( t \). Czas \( T \) nazywamy okresem sygnału, \( k \) jest liczbą całkowitą. W każdej chwili czasu \( t \) przesunięcie na osi czasu o okres lub jego wielokrotność nie zmienia wartości sygnału. Odwrotność okresu podstawowego nazywamy częstotliwością sygnału:

Jednostką częstotliwości jest herc (jeden Hz stanowi pojedynczą oscylację, okres lub cykl na sekundę). Częstotliwością kątową (pulsacją) nazywamy szybkość zmiany fazy sygnału okresowego w czasie:

Częstotliwość kątową określa się w radianach na sekundę (rd/s).

Gdy sygnał jest okresowy o okresie \( T \), uśrednianie w czasie nieskończonym jest równoważne uśrednianiu za okres. Wtedy wartością średnią ciągłego sygnału okresowego \( x(t) \) jest:

gdzie \( t_0 \) jest dowolną chwilą. Moc średnia ciągłego sygnału okresowego jest równa mocy średniej w jednym okresie \( T \):

dla dowolnej chwili \( t_0 \). Jeżeli energia sygnału okresowego, przypadająca na pojedynczy okres \( T \), jest różna od zera, to całkowita energia sygnału \( E_x \) jest nieskończona.

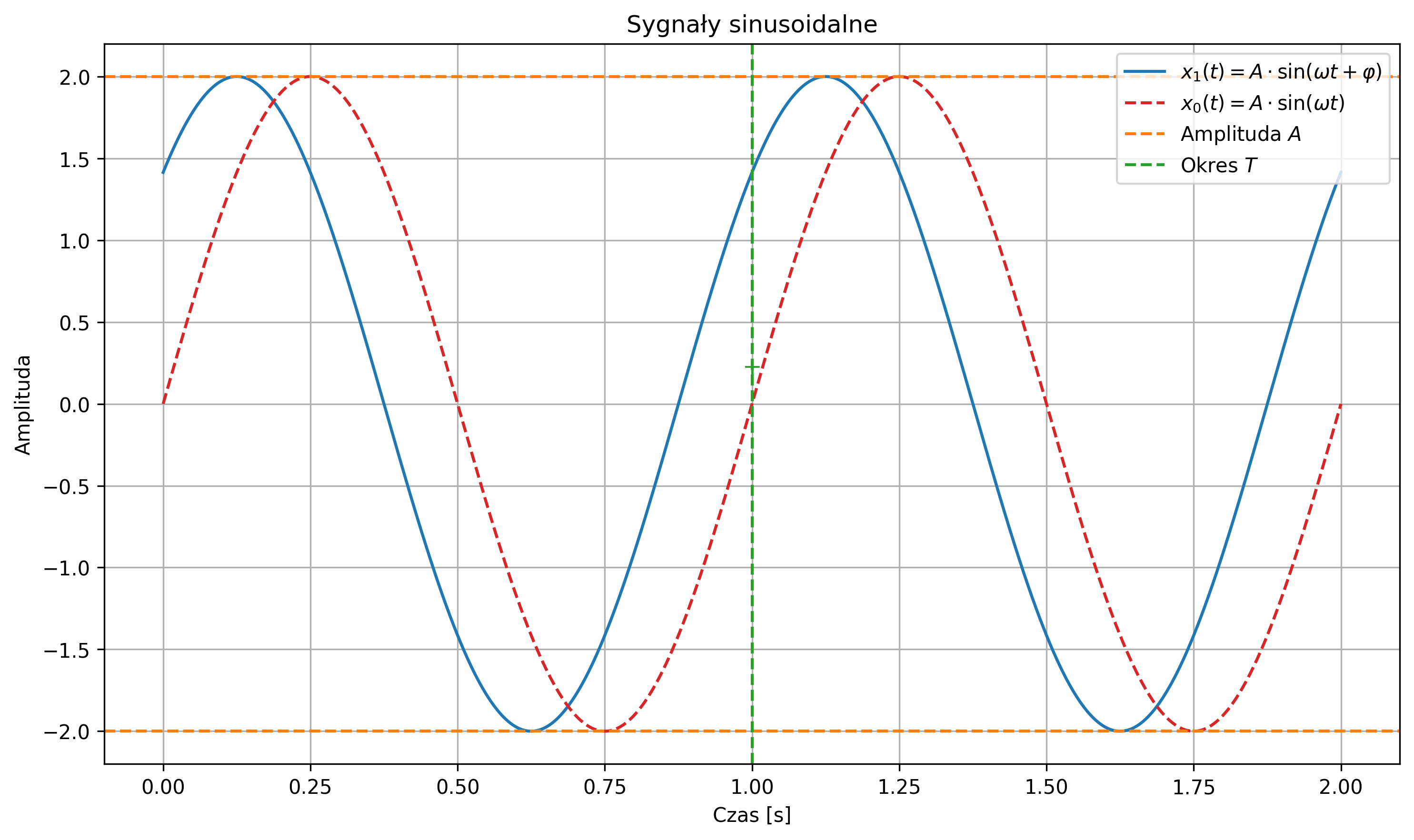
Najbardziej znanym sygnałem okresowym jest sygnał sinusoidalny (rys. 2.9):

gdzie:

• \( A \) to amplituda sygnału,
• \( \omega \) to pulsacja sygnału,
• \( f \) to częstotliwość sygnału,
• \( \varphi \) to faza sygnału.

Wartość średnia sygnału sinusoidalnego wynosi \( 0 \) (w rzeczywistości \( \approx 0 \)), zaś jego moc średnia zależy tylko od amplitudy i jest równa \( A^2 / 2 \). Suma sygnałów sinusoidalnych o różnych częstotliwościach jest także sygnałem okresowym. Stanowi to istotny fakt przy analizie częstotliwościowej sygnałów.