2. Sygnały i ich charakterystyki

2.8. Reprezentacja sygnałów w języku Python

Celem poniższych ćwiczeń jest zapoznanie się z wybranymi typami sygnałów oraz nabycie praktycznych umiejętności w generowaniu i wizualizacji ich przebiegów, a także poznanie podstawowych funkcji i komend w języku Python przydatnych w analizie sygnałów.

Poniższe przykłady przedstawiają pełne kody źródłowe w języku Python, opracowane na potrzeby realizacji poszczególnych zadań. Do wykonania przedstawionych zadań wymagane jest wykorzystanie następujących bibliotek języka Python:


import numpy as np                # obliczenia numeryczne i tablice
import matplotlib.pyplot as plt   # tworzenie wykresów ciągłych i dyskretnych
import scipy.signal as signal     # generowanie standardowych sygnałów,                              
                                  # takich jak np. prostokątny, trójkątny, piłokształtny 

oraz wymagana jest znajomość między innymi następujących poleceń i funkcji języka Python:


np.arange, np.linspace            # tworzenie wektorów czasu
plt.figure, plt.plot, plt.stem    # rysowanie wykresów ciągłych i dyskretnych
plt.grid, plt.xlabel, plt.ylabel, plt.title, plt.legend  # oznaczanie osi, tytułów, legend i siatki
np.sin, np.exp, np.pi             # generowanie sygnałów sinusoidalnych, wykładniczych, stała pi
signal.square, signal.sawtooth, signal.chirp   # generowanie sygnałów specjalnych

W zadaniach będziemy łączyć te funkcje w celu generowania, wizualizacji i analizy różnych typów sygnałów. Poniżej znajdują się ćwiczenia z przykładową implementacją. Autor zachęca czytelnika do samodzielnego uruchamiania kodów oraz do eksperymentowania z różnymi parametrami sygnałów poprzez ich modyfikację. 

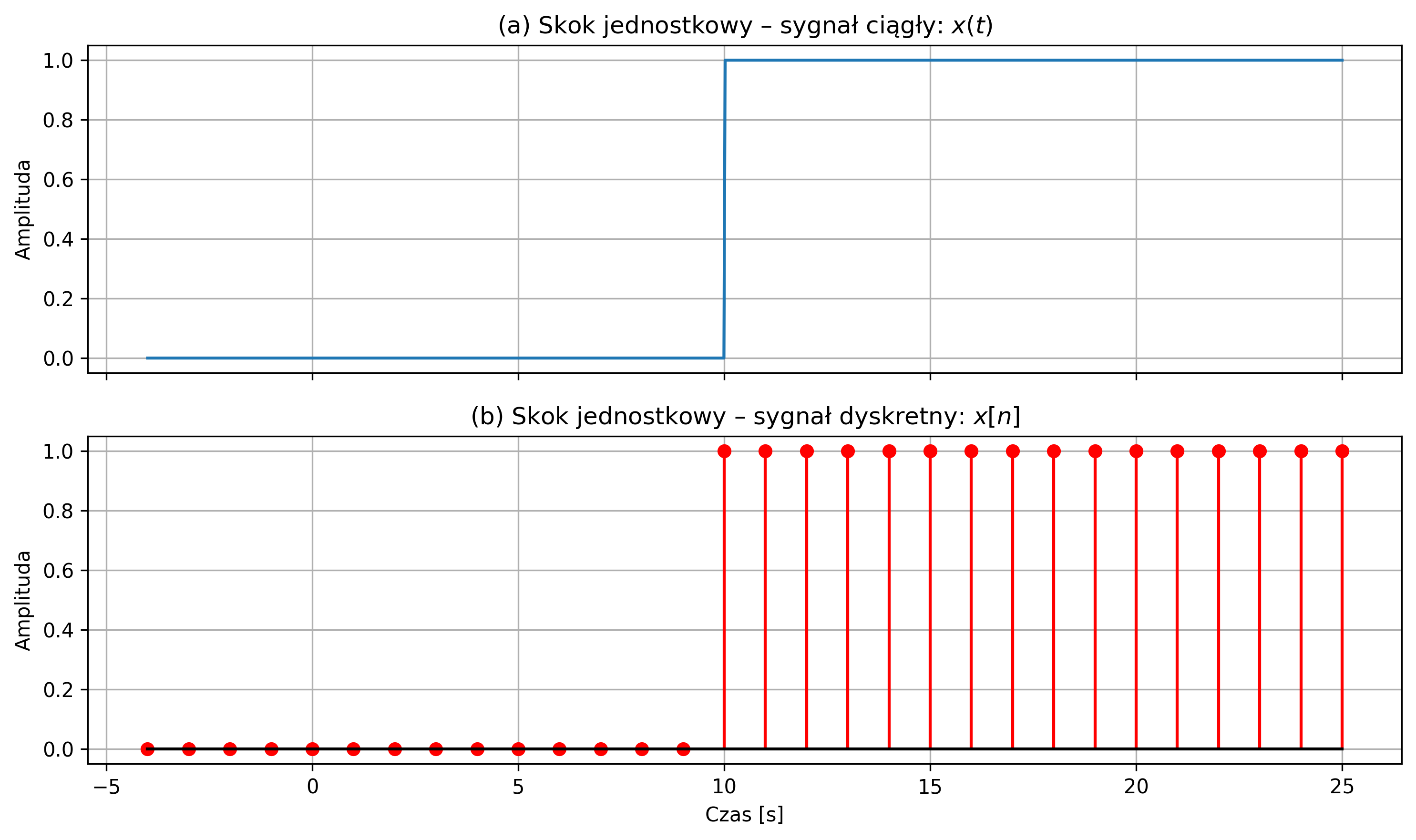
Wygenerować skok jednostkowy określony przez następujące równanie:

\( x(t) = \begin{cases} 1, & \text{gdy } t \ge 10 \\ 0, & \text{gdy } t < 10 \end{cases} \)

Narysować sygnał ciągły \(x(t)\) i jego wersję dyskretną \(x[n]\) dla \(N = 30\) próbek przy częstotliwości próbkowania \(f_s = 1\) Hz.


import numpy as np
import matplotlib.pyplot as plt

# Parametry sygnału
fs = 1                     # częstotliwość próbkowania [Hz]
T = 1 / fs                 # okres próbkowania
n = np.arange(-4, 26)      # 30 próbek: od -4 do 25

# Sygnał dyskretny: skok jednostkowy
x_disc = np.where(n >= 10, 1, 0)

# Sygnał ciągły (z większą rozdzielczością)
t_cont = np.linspace(-4, 25, 1000)
x_cont = np.where(t_cont >= 10, 1, 0)

# Tworzenie dwóch wykresów
fig, axs = plt.subplots(2, 1, figsize=(10, 6), sharex=True)

# Wykres 1: sygnał ciągły
axs[0].plot(t_cont, x_cont)
axs[0].set_title(r'(a) Skok jednostkowy – sygnał ciągły: $x(t)$')
axs[0].set_ylabel("Amplituda")
axs[0].grid(True)

# Wykres 2: sygnał dyskretny
axs[1].stem(n, x_disc, linefmt='r-', markerfmt='ro', basefmt='k-')
axs[1].set_title(r'(b) Skok jednostkowy – sygnał dyskretny: $x[n]$')
axs[1].set_xlabel('Czas [s]')
axs[1].set_ylabel('Amplituda')
axs[1].grid(True)

plt.tight_layout()
plt.show()

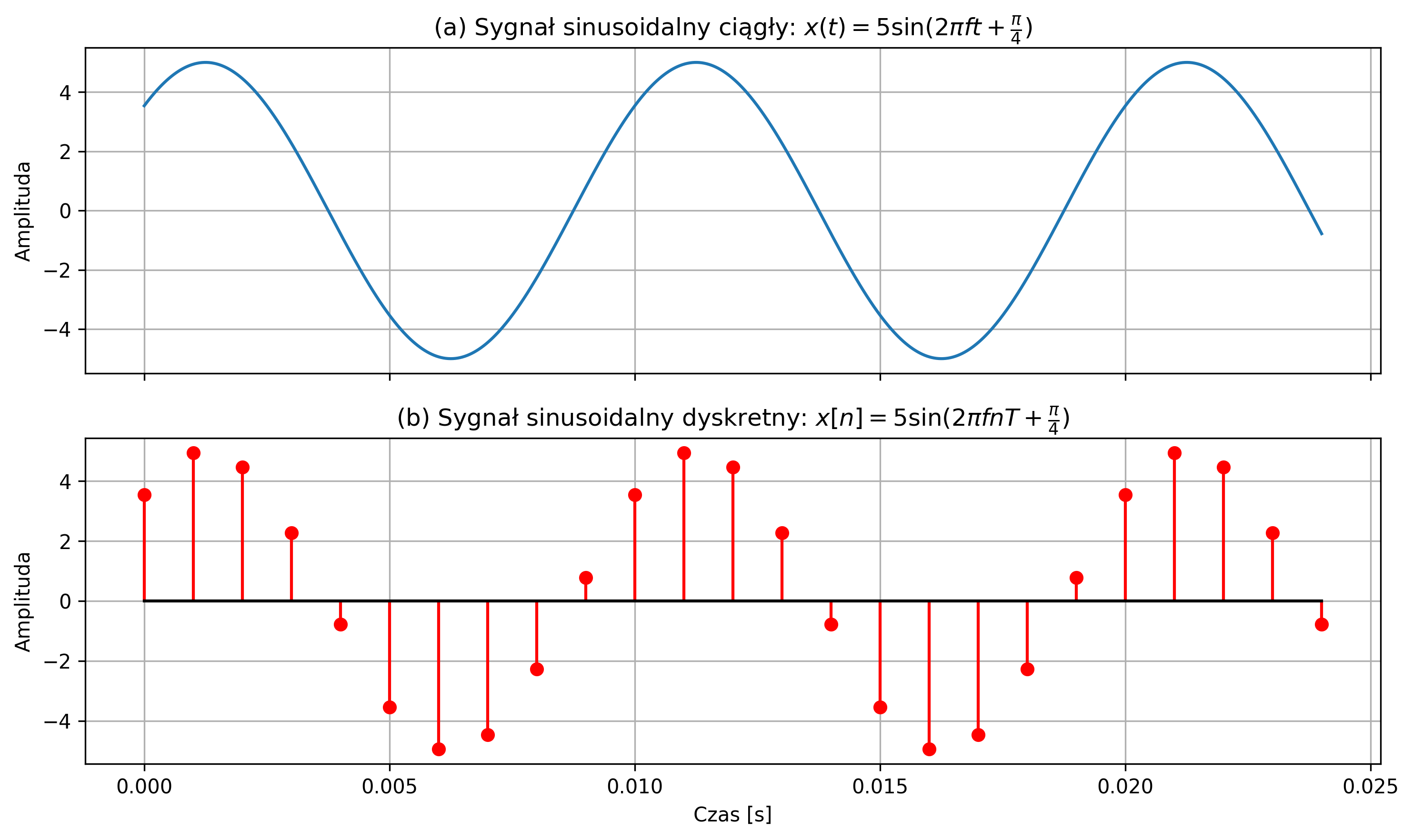
Wygenerować sygnał sinusoidalny określony przez następujące równanie:

\( x(t) = A \sin(2\pi f t + \varphi) \)

o amplitudzie \( A = 5 \), częstotliwości sygnału \( f = 100 \) Hz i przesunięciu fazowym \( 45^{\circ} \). Narysować sygnał ciągły \(x(t)\) i jego wersję dyskretną \(x[n]\) dla \( N = 25 \) próbek, przyjmując częstotliwość próbkowania \( f_s =1000 \) Hz. Dodatkowo, sporządzić wspólny wykres sygnału ciągłego i dyskretnego na jednym rysunku.


import numpy as np
import matplotlib.pyplot as plt

# Parametry sygnału
fs = 1000         # częstotliwość próbkowania [Hz]
N = 25            # liczba próbek
A = 5             # amplituda
f = 100           # częstotliwość sygnału [Hz]
T = 1 / fs        # okres próbkowania
phi = np.pi / 4   # przesunięcie fazowe [rad]

# Oś czasu: ciągła i dyskretna
t_cont = np.linspace(0, (N - 1) / fs, 1000) 
n = np.arange(N)
t_disc = n * T    

# Sygnały
x_cont = A * np.sin(2 * np.pi * f * t_cont + phi)  # sygnał ciągły
x_disc = A * np.sin(2 * np.pi * f * t_disc + phi)  # sygnał dyskretny

# Tworzenie dwóch wykresów
fig, axs = plt.subplots(2, 1, figsize=(10, 6), sharex=True)

# Wykres 1: sygnał ciągły
axs[0].plot(t_cont, x_cont)
axs[0].set_title(r'(a) Sygnał sinusoidalny ciągły: $x(t) =5\sin(2\pi f t + \frac{\pi}{4})$')
axs[0].set_ylabel('Amplituda')
axs[0].grid(True)

# Wykres 2: sygnał dyskretny
axs[1].stem(t_disc, x_disc, linefmt='r-', markerfmt='ro', basefmt='k-')
axs[1].set_title(r'(b) Sygnał sinusoidalny dyskretny: $x[n] = 5\sin(2\pi f nT + \frac{\pi}{4})$')
axs[1].set_xlabel('Czas [s]')
axs[1].set_ylabel('Amplituda')
axs[1].grid(True)

plt.tight_layout()
plt.show()

W wersji wspólnego wykresu:
 

import numpy as np
import matplotlib.pyplot as plt

# Parametry sygnału
fs = 1000        # częstotliwość próbkowania [Hz]
N = 25           # liczba próbek
A = 5            # amplituda
f = 50           # częstotliwość sygnału [Hz]
T = 1 / fs       # okres próbkowania
phi = np.pi / 4  # przesunięcie fazowe [rad]

# Oś czasu: ciągła i dyskretna
t_cont = np.linspace(0, (N - 1) / fs, 1000)  
n = np.arange(N)
t_disc = n * T               

# Sygnały
x_cont = A * np.sin(2 * np.pi * f * t_cont + phi)  # sygnał ciągły
x_disc = A * np.sin(2 * np.pi * f * t_disc + phi)  # sygnał dyskretny

# Wykres
plt.figure(figsize=(10, 4))
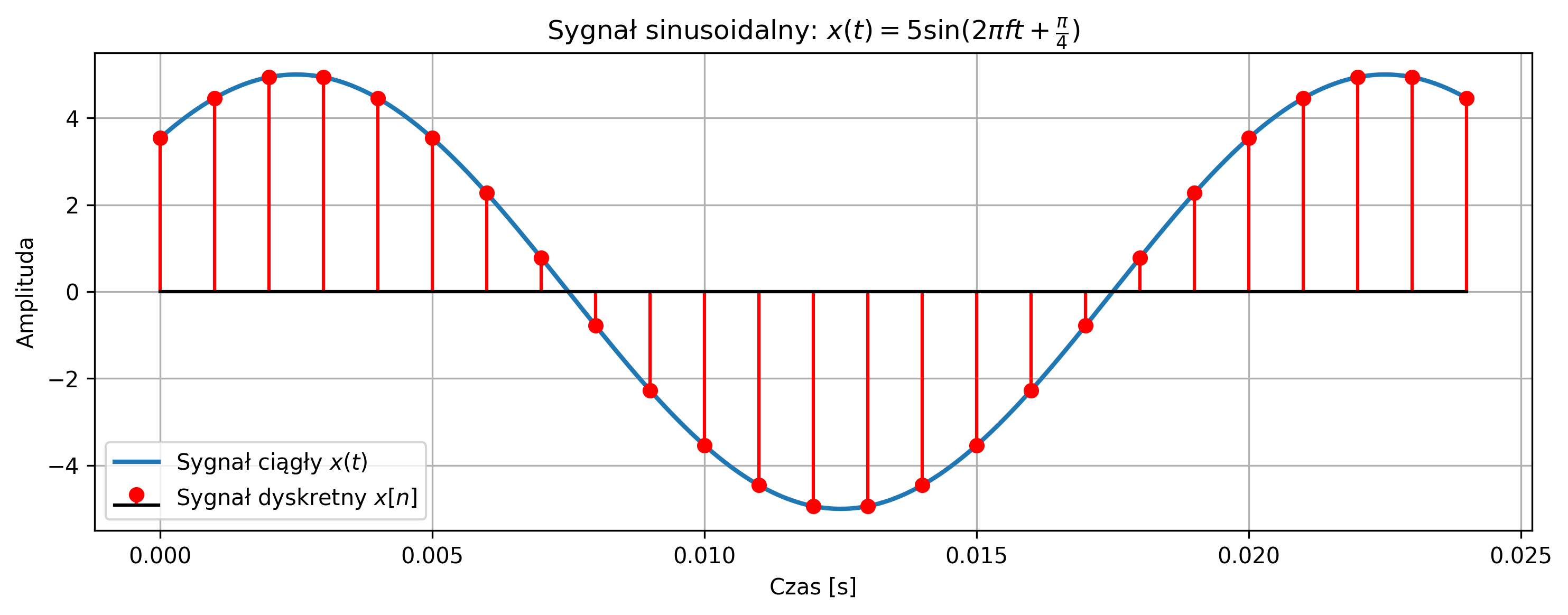
plt.plot(t_cont, x_cont, label=r'Sygnał ciągły $x(t)$', linewidth=2)
plt.stem(t_disc, x_disc, linefmt='r-', markerfmt='ro', basefmt='k-', label=r'Sygnał dyskretny $x[n]$')
plt.title(r'Sygnał sinusoidalny: $x(t) = 5\sin(2\pi f t + \frac{\pi}{4})$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

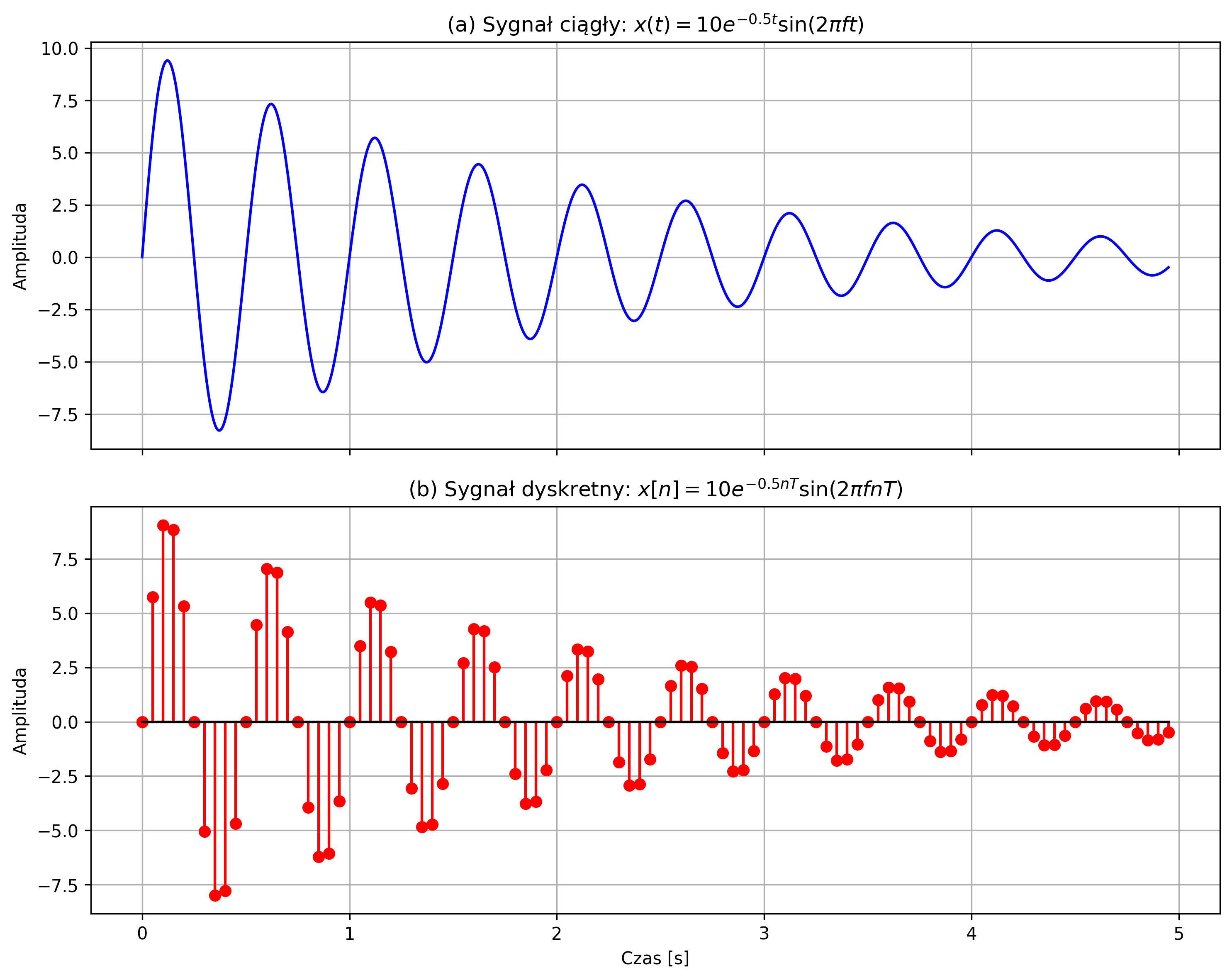
Wygenerować sygnał sinusoidalny tłumiony wykładniczo opisany równaniem:

\( x(t) = A e^{-0.5 t}\sin(2\pi f t)\quad \text{dla } t \ge 0 \)

dla amplitudy \( A = 10 \), częstotliwości sygnału sinusoidalnego \( f = 2 \) Hz i współczynnika tłumienia \(\alpha = 0.5 \).  Narysować sygnał ciągły \( x(t) \) i jego wersję dyskretną \( x[n] \) dla \( N = 100 \) próbek, przyjmując częstotliwość próbkowania \( f_s = 20 \) Hz.


import numpy as np
import matplotlib.pyplot as plt

# Parametry sygnału
A = 10            # amplituda
f = 2             # częstotliwość sinusoidy [Hz]
alpha = 0.5       # tłumienie wykładnicze [1/s]
N = 100           # liczba próbek
fs = 20           # częstotliwość próbkowania [Hz]
T = 1 / fs        # okres próbkowania

# Sygnał ciągły
t_cont = np.linspace(0, (N - 1) * T, 1000)
x_cont = A * np.exp(-alpha * t_cont) * np.sin(2 * np.pi * f * t_cont)

# Sygnał dyskretny
n = np.arange(N)
t_disc = n * T
x_disc = A * np.exp(-alpha * t_disc) * np.sin(2 * np.pi * f * t_disc)

# Tworzenie dwóch wykresów
fig, axs = plt.subplots(2, 1, figsize=(10, 8), sharex=True)

# Wykres 1: sygnał ciągły
axs[0].plot(t_cont, x_cont, color='blue')
axs[0].set_title(r'(a) Sygnał ciągły: $x(t) = 10e^{-0.5t}\sin(2\pi f t)$', fontsize=12)
axs[0].set_ylabel('Amplituda')
axs[0].grid(True)

# Wykres 2: sygnał dyskretny
axs[1].stem(t_disc, x_disc, linefmt='r-', markerfmt='ro', basefmt='k-')
axs[1].set_title(r'(b) Sygnał dyskretny: $x[n] = 10e^{-0.5nT}\sin(2\pi f nT)$', fontsize=12)
axs[1].set_xlabel('Czas [s]')
axs[1].set_ylabel('Amplituda')
axs[1].grid(True)

plt.tight_layout()
plt.show()

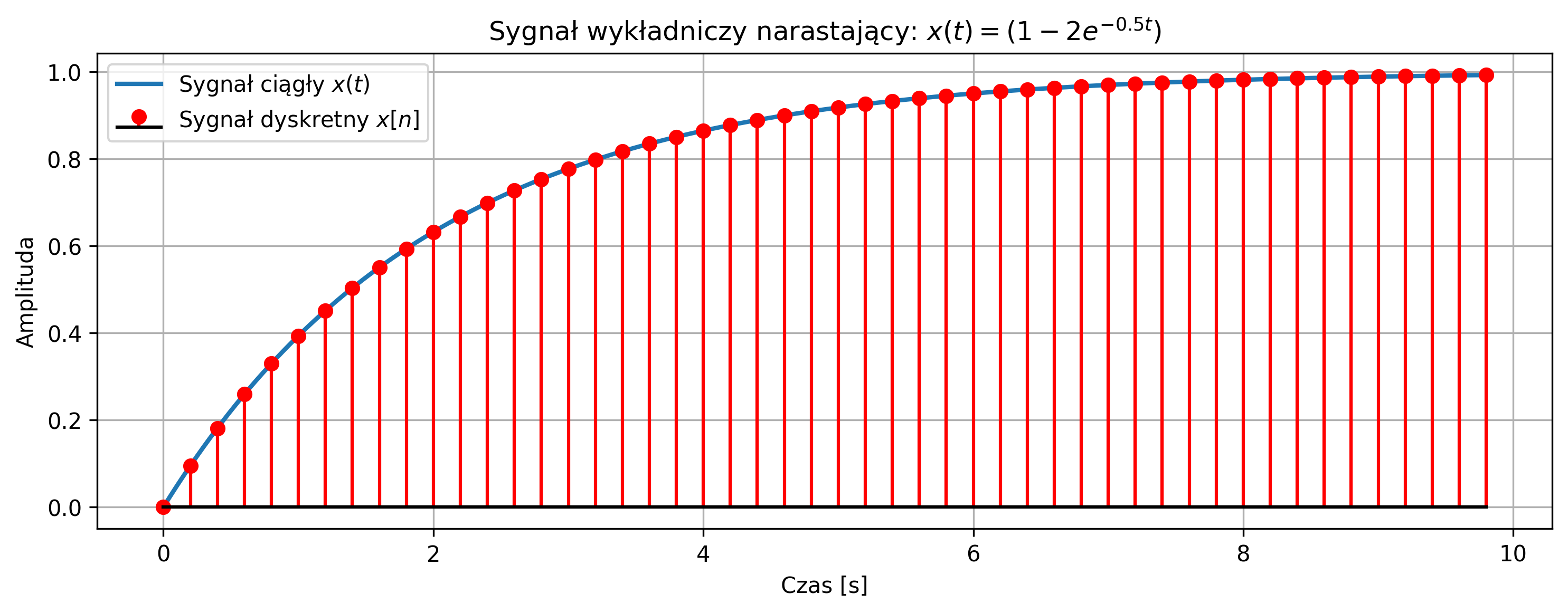
Wygenerować sygnał wykładniczy narastający określony przez następujące równanie:

\( x(t) = \bigl(1 - e^{-0.5 t}\bigr)\mathbf{1}(t) \)

Narysować na jednym wykresie sygnał ciągły \( x(t) \) oraz jego wersję dyskretną \( x[n] \) dla \( N = 50 \) próbek, przy częstotliwości próbkowania \( f_s = 5\text{ Hz} \).


import numpy as np
import matplotlib.pyplot as plt

# Parametry sygnału
fs = 5              # częstotliwość próbkowania [Hz]
N = 50              # liczba próbek
alpha = -0.5        # wykładnik 
T = 1 / fs          # okres próbkowania
t_max = (N - 1) / fs

# Czas ciągły i dyskretny
t_cont = np.linspace(0, t_max, 1000)
n = np.arange(N)
t_disc = n * T  

x_cont = (1 - np.exp(alpha * t_cont))  
x_disc = (1 - np.exp(alpha * t_disc))

# Wspólny wykres
plt.figure(figsize=(10, 4))
plt.plot(t_cont, x_cont, label=r'Sygnał ciągły $x(t)$', linewidth=2)
plt.stem(t_disc, x_disc, linefmt='r-', markerfmt='ro', basefmt='k-', label=r'Sygnał dyskretny $x[n]$')
plt.title(r'Sygnał wykładniczy narastający: $x(t) = \left(1 - 2e^{-0.5t}\right)$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

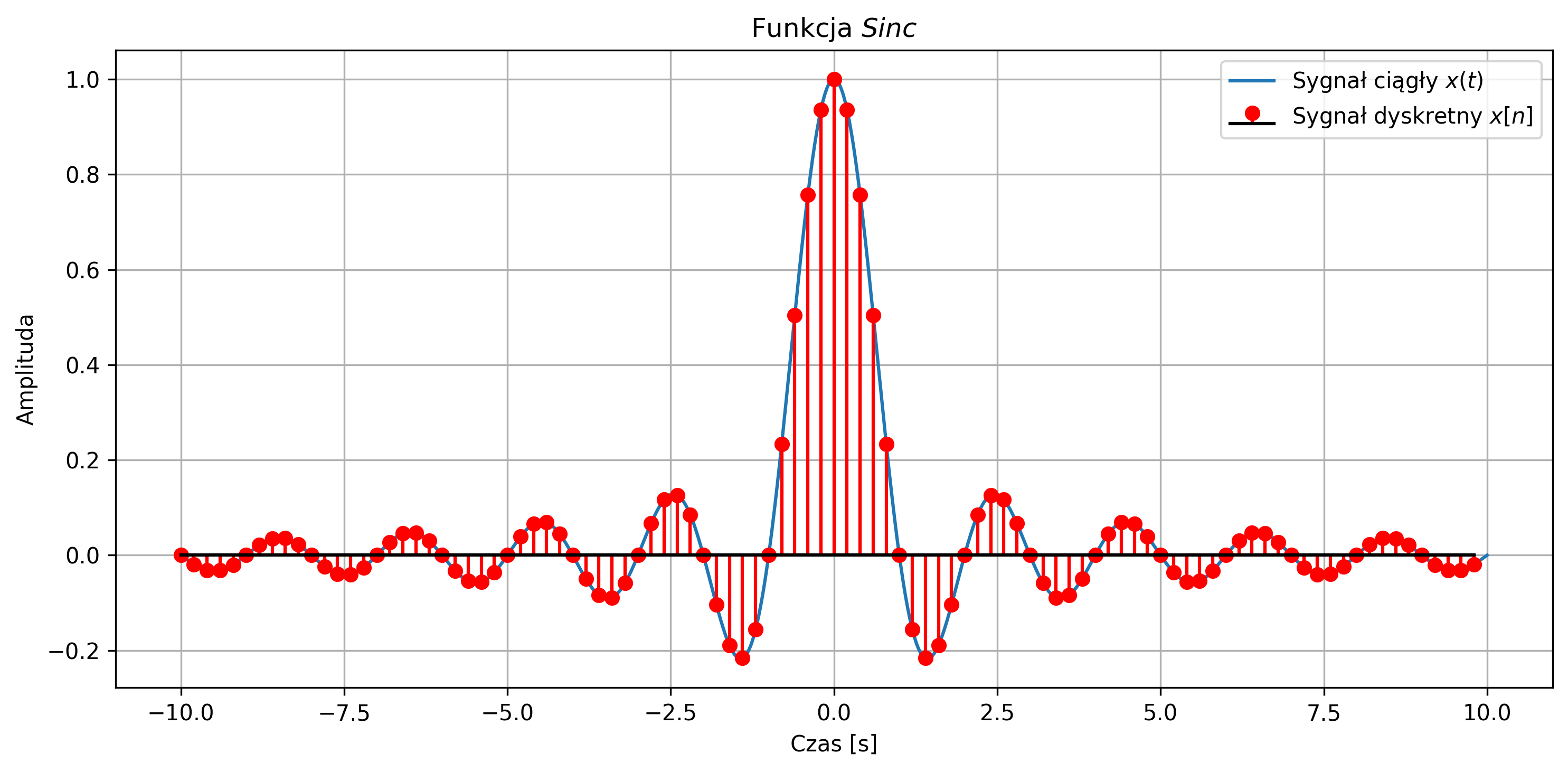
Wygenerować sygnał \(Sinc \) opisany równaniem:

\( x(t) = \begin{cases}\dfrac{\sin(2\pi f t)}{2\pi f t}, & \text{gdy } t \neq 0 \\[4pt] 1, & \text{gdy } t = 0 \end{cases} \)

dla częstotliwości sygnału sinusoidalnego \( f = 1 \) Hz. Narysować wspólny wykres sygnału ciągłego \(x(t)\) i dyskretnego \(x[n]\) dla \(N = 100\) próbek, przyjmując częstotliwość próbkowania \(f_s = 5\) Hz.


import numpy as np
import matplotlib.pyplot as plt

# Parametry sygnału
f = 1               # częstotliwość sygnału
fs = 5              # częstotliwość próbkowania
N = 100             # liczba próbek
T = 1 / fs

# Oś czasu - ciągła i dyskretna
t_cont = np.linspace(-10, 10, 1000) 
n = np.arange(-N//2, N//2)
t_disc = n * T  

# Funkcja Sinc - ciągła i dyskretna
y_cont = np.sinc(f * t_cont)
y_disc = np.sinc(f * t_disc)

# Wspólny wykres
plt.figure(figsize=(10, 5))

# Wersja ciągła i dyskretna
plt.plot(t_cont, y_cont, label=r'Sygnał ciągły $x(t)$')
plt.stem(t_disc, y_disc, linefmt='r-', markerfmt='ro', basefmt='k-', label=r'Sygnał dyskretny $x[n]$')

plt.title(r'Funkcja $Sinc$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
 
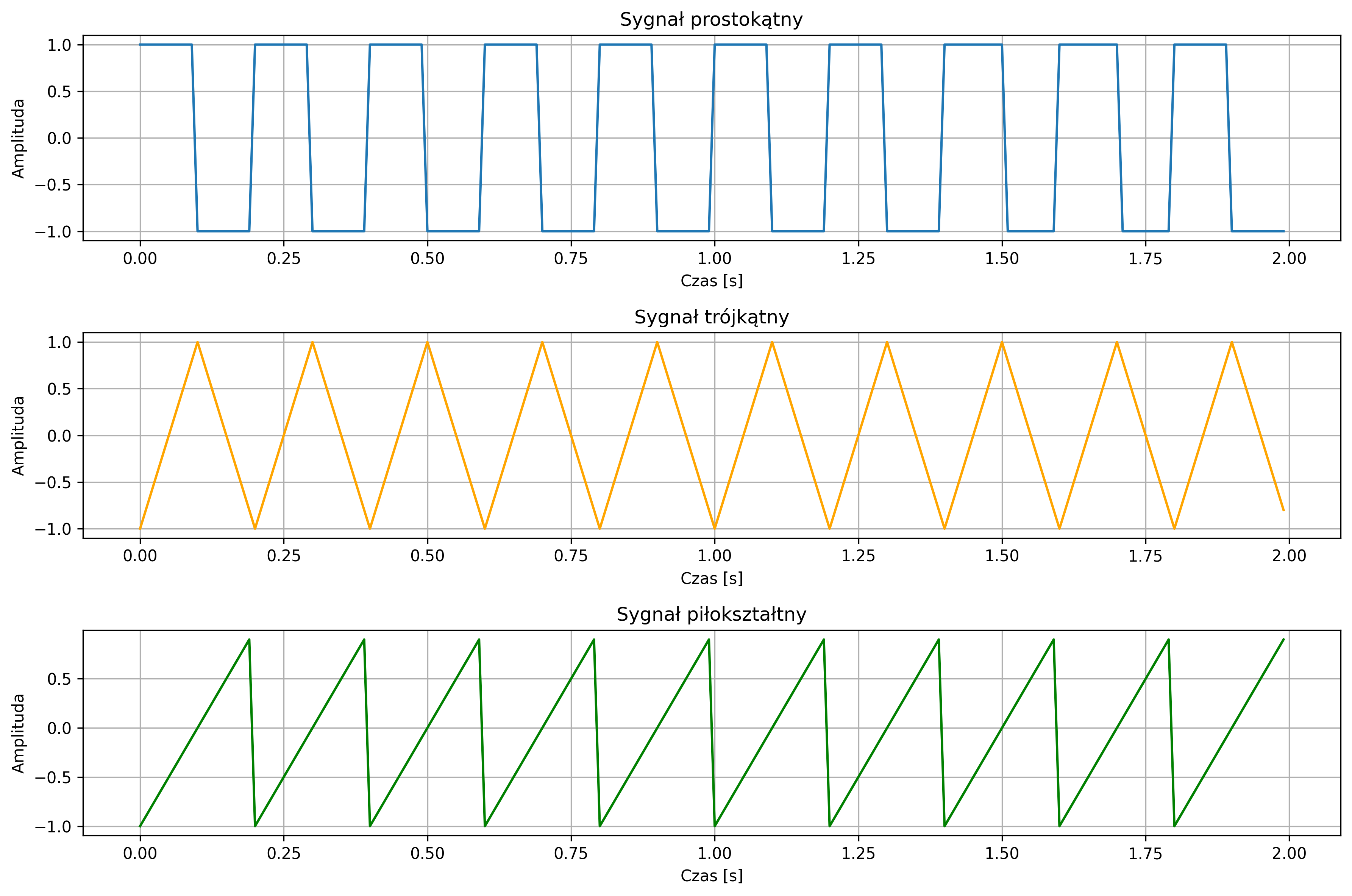
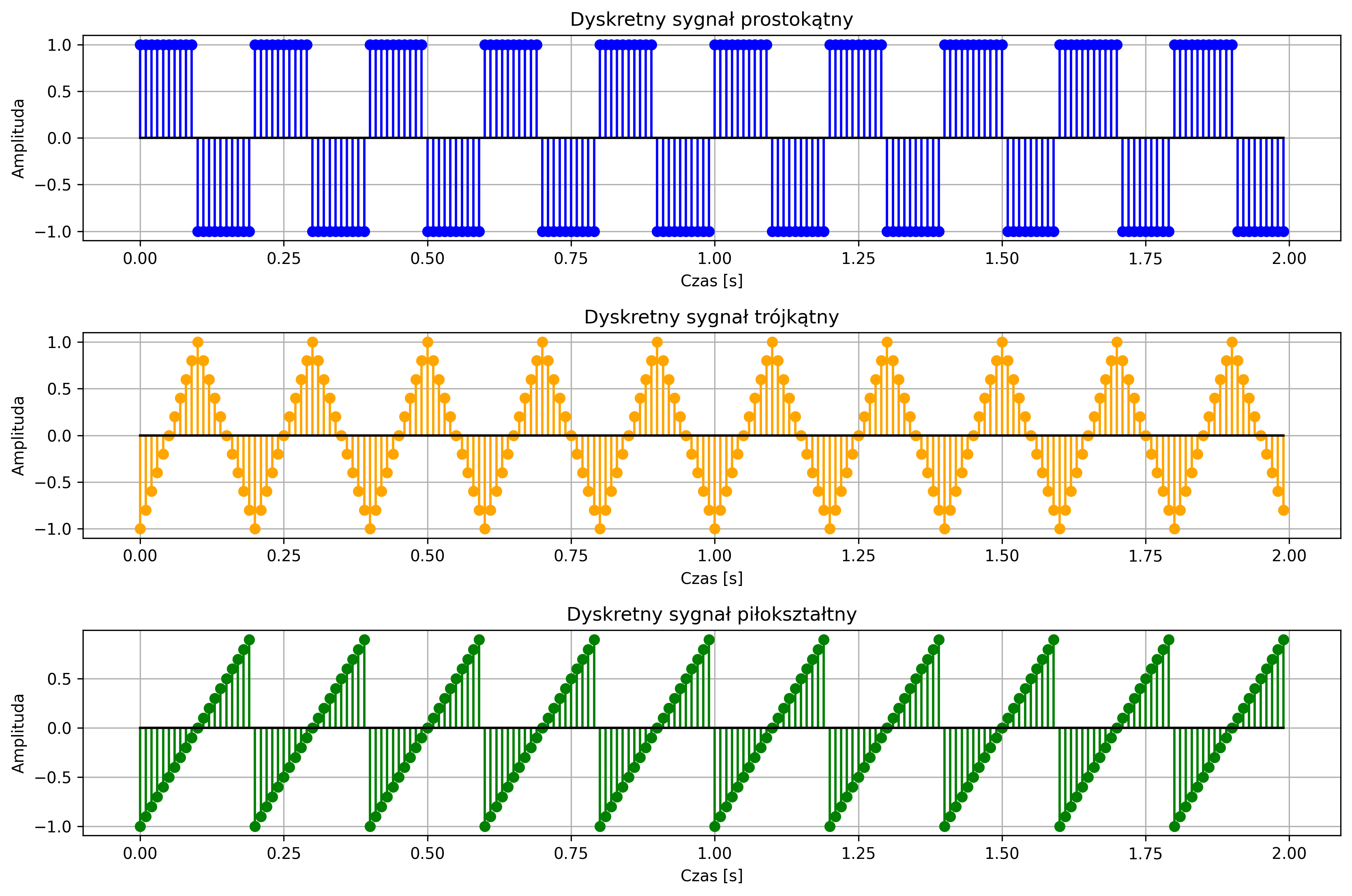
Funkcja \(Sinc\) odgrywa istotną rolę w przetwarzaniu sygnałów. Pojawia się zarówno w filtracji dolnoprzepustowej, jak i w zagadnieniach próbkowania sygnałów zgodnie z twierdzeniem Nyquista-Shannona. Jej kształt odpowiada odpowiedzi impulsowej idealnego filtru dolnoprzepustowego, natomiast w dziedzinie częstotliwości jest reprezentowana przez prostokątny wycinek pasma. W zastosowaniach praktycznych funkcję \(Sinc\) należy ograniczać za pomocą funkcji okna, co powoduje pojawienie się oscylacji - tzw. zjawisko Gibbsa. Zagadnienia te zostaną omówione w rozdziale 3.

Wygenerować sygnały prostokątny, trójkątny oraz piłokształtny dla częstotliwości \(f = 5\ \text{Hz}\). Dla każdego sygnału narysować wersję ciągłą \(x(t)\) i dyskretną \(x[n]\) dla \(N = 200\) próbek, przyjmując częstotliwość próbkowania \(f_s = 100 \) Hz.


import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# Parametry sygnałów
fs = 100          # częstotliwość próbkowania [Hz]
f = 5             # częstotliwość sygnału [Hz]
N = 200           # liczba próbek
T = N / fs        # czas trwania sygnału [s]

# Oś czasu
t = np.linspace(0, T, N, endpoint=False)

# Sygnał prostokątny
rect_signal = signal.square(2 * np.pi * f * t, duty=0.5) # duty musi mieścić się w [0,1].

# Sygnał trójkątny
tri_signal = signal.sawtooth(2 * np.pi * f * t, width=0.5)  # width=0.5 daje trójkąt

# Sygnał piłokształtny (piłowy)
saw_signal = signal.sawtooth(2 * np.pi * f * t, width=1)    # width=1 daje piłę

# Rysowanie wykresów
plt.figure(figsize=(12, 8))

plt.subplot(3,1,1)
plt.plot(t, rect_signal, label='Sygnał prostokątny')
plt.title('Sygnał prostokątny')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)

plt.subplot(3,1,2)
plt.plot(t, tri_signal, label='Sygnał trójkątny', color='orange')
plt.title('Sygnał trójkątny')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)

plt.subplot(3,1,3)
plt.plot(t, saw_signal, label='Sygnał piłokształtny', color='green')
plt.title('Sygnał piłokształtny')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)

plt.tight_layout()
plt.show()
W wersji dyskretnej:
 

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# Parametry sygnałów
fs = 100          # częstotliwość próbkowania [Hz]
f = 5             # częstotliwość sygnału [Hz]
N = 200           # liczba próbek
T = N / fs        # czas trwania sygnału [s]

# Oś czasu dyskretna
n = np.arange(N)
t = n / fs

# Sygnały dyskretne
rect_signal = signal.square(2 * np.pi * f * t, duty=0.5)
tri_signal = signal.sawtooth(2 * np.pi * f * t, width=0.5)
saw_signal = signal.sawtooth(2 * np.pi * f * t, width=1)

# Rysowanie wykresów
plt.figure(figsize=(12, 8))

plt.subplot(3,1,1)
plt.stem(t, rect_signal, linefmt='b-', markerfmt='bo', basefmt='k-')
plt.title('Dyskretny sygnał prostokątny')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)

plt.subplot(3,1,2)
plt.stem(t, tri_signal, linefmt='orange', markerfmt='o', basefmt='k-')
plt.title('Dyskretny sygnał trójkątny')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)

plt.subplot(3,1,3)
plt.stem(t, saw_signal, linefmt='green', markerfmt='o', basefmt='k-')
plt.title('Dyskretny sygnał piłokształtny')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)

plt.tight_layout()
plt.show()

Wygenerować sygnał świergotowy (chirp) o częstotliwości liniowo rosnącej od \(1\) Hz do \(400\) Hz.  Przyjąć czas trwania sygnału \(0.1\) sekundy oraz częstotliwość próbkowania \(f_s = 10\ 000\) Hz. Narysować wykres sygnału ciągłego \(x(t)\).


import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import chirp

# Parametry
t = np.linspace(0, 0.1, 10000)  # czas trwania  0.1 [s]

# Generowanie sygnału świergotowego liniowego od 1 do 400 Hz
x = chirp(t, f0=1, f1=400, t1=0.1, method='linear') 
        # f0 = 1     częstotliwość początkowa [Hz]
        # f1 = 400   częstotliwość końcowa [Hz]
        # t1 = 0.1   czas, w którym osiągana jest f1

plt.figure(figsize=(10, 3))
plt.plot(t, x)
plt.title('Sygnał świergotowy liniowy, 1-400 Hz')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.tight_layout()
plt.show()

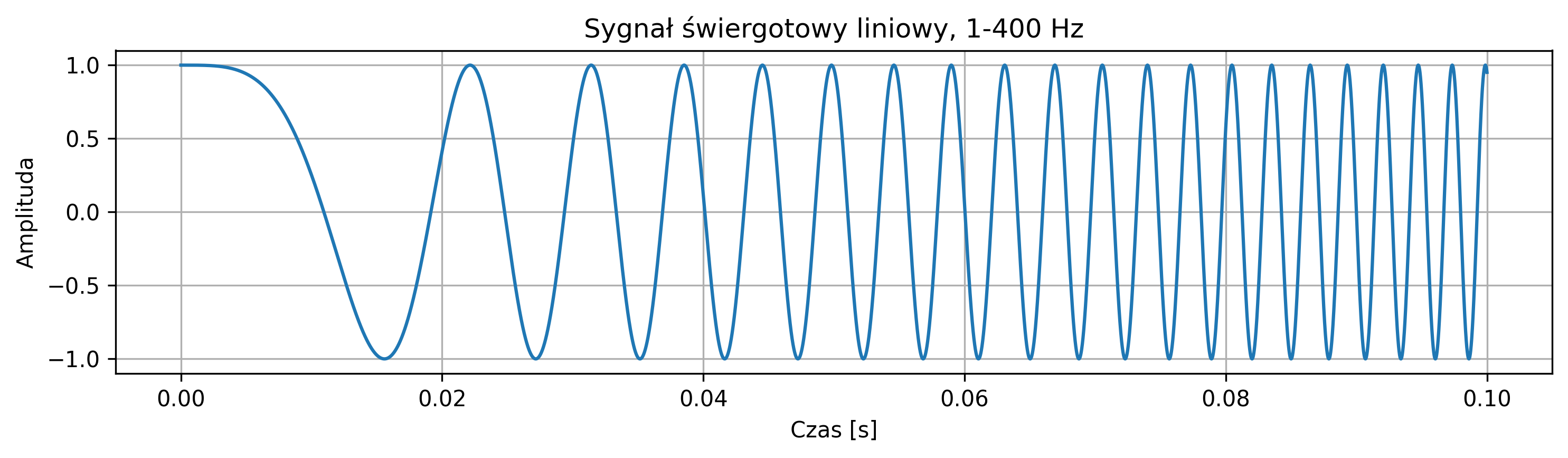
Sygnał świergotowy to sygnał o zmiennej częstotliwości chwilowej. Najprostszym jego przypadkiem jest sygnał sinusoidalny, którego częstotliwość chwilowa jest przestrajana w trakcie generowania. Przestrajanie częstotliwości odbywa się zwykle w sposób liniowy lub logarytmiczny. Sygnały świergotowe stosuje się m.in. do analizy charakterystyk częstotliwościowych urządzeń (np. filtrów, wzmacniaczy, głośników), do wyznaczania odpowiedzi systemu na różne częstotliwości w krótkim czasie, a także do badania reakcji układów biologicznych na bodźce o zmiennej częstotliwości.

Po zapoznaniu się z możliwościami generowania podstawowych sygnałów, możemy prześledzić operację splotu oraz zagadnienia związane z wyznaczaniem odpowiedzi impulsowej systemów LTI.

 

Wymagana jest znajomość funkcji:


np.convolve    # obliczanie splotu dwóch jednowymiarowych sygnałów dyskretnych
               # funkcja z biblioteki NumPy, przeznaczona głównie do prostych operacji na wektorach
  
convolve       # obliczanie splotu sygnałów (1D, 2D i wyższych wymiarów) 
               # funkcja z biblioteki scipy.signal, oferująca większe możliwości

dzięki którym można łatwo wykonać operację splotu, np. w celu wyznaczenia odpowiedzi impulsowej systemów LTI.

Obliczyć splot dwóch ciągów próbek sygnałów: \( X = [2,4,6] \) oraz \( Y = [1,2] \).

Zgodnie z zasadą obliczenia splotu, opisaną w rozdziale 2.4, najpierw odwracamy ciąg próbek \( Y \) w czasie i wyrównujemy go z ciągiem próbek \( X \) tak, aby ostatnia próbka \( Y \) po odwróceniu pokrywała się z pierwszą próbką \( X\). Następnie mnożymy przez siebie pokrywające się próbki i sumujemy wyniki, co daje pierwszą wartość splotu.

X         2  4  6      2 * 1 = 2

Y      2  1            splot = [2]

Odwrócony ciąg próbek \( Y \) przesuwamy w prawo o jedno miejsce i powtarzamy operację:

X     2  4  6      2 * 2 + 4 * 1 = 8

Y     2  1         splot = [2 8]

Następnie przesuwamy ciąg próbek \( Y \) ponownie:

X     2  4  6       4 * 2 + 6 * 1 = 14

Y        2  1       splot = [2 8 14]

Jeżeli żadne próbki sygnałów nie pokrywają się, to kończymy obliczenia:

X     2  4  6         6 * 2 = 12

Y           2  1      splot = [2 8 14 12]

Operacja splotu jest przemienna, co oznacza, że otrzymamy ten sam wynik, jeśli odwrócimy próbki \( X \) i przesuwamy próbki \( Y \). Taki wynik możemy uzyskać w Pythonie:


import numpy as np

X = [2, 4, 6]
Y = [1, 2]

splot = np.convolve(X, Y)
print('Wynik splotu:', splot)
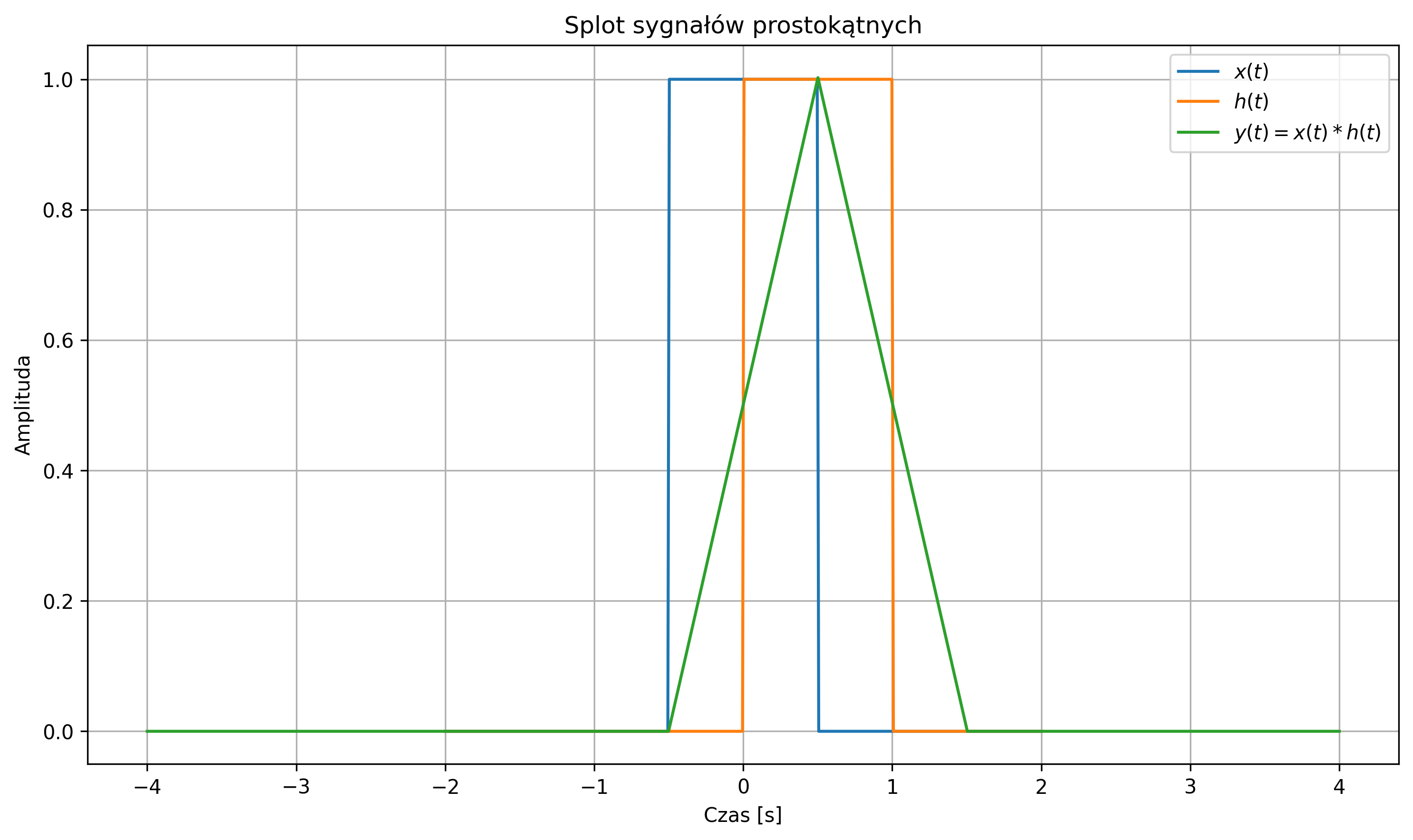
Wyznacz splot dwóch impulsów prostokątnych - pierwszy impuls trwa w zakresie \( [-0.5,0.5] \) sekundy, drugi impuls jest przesunięty w prawo o \( 0.5 \) sekundy względem pierwszego.
 


import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import convolve  # obliczanie splotu dwóch sygnałów 

# Definicja impulsu prostokątnego
def rect(t):
    return np.where(np.abs(t) <= 0.5, 1, 0)

# Osie czasu
t = np.linspace(-2, 2, 400)
dt = t[1] - t[0]

# Sygnały
x = rect(t)        # impuls prostokątny 
h = rect(t - 0.5)  # przesunięty impuls prostokątny

# Splot ciągły (jako dyskretny z krokiem dt)
y = convolve(x, h, mode='full') * dt
t_y = np.linspace(t[0]+t[0], t[-1]+t[-1], len(y))

# Wykresy
plt.figure(figsize=(10,6))
plt.plot(t, x, label='$x(t)$')
plt.plot(t, h, label='$h(t)$')
plt.plot(t_y, y, label='$y(t) = x(t)*h(t)$')
plt.title('Splot sygnałów prostokątnych')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
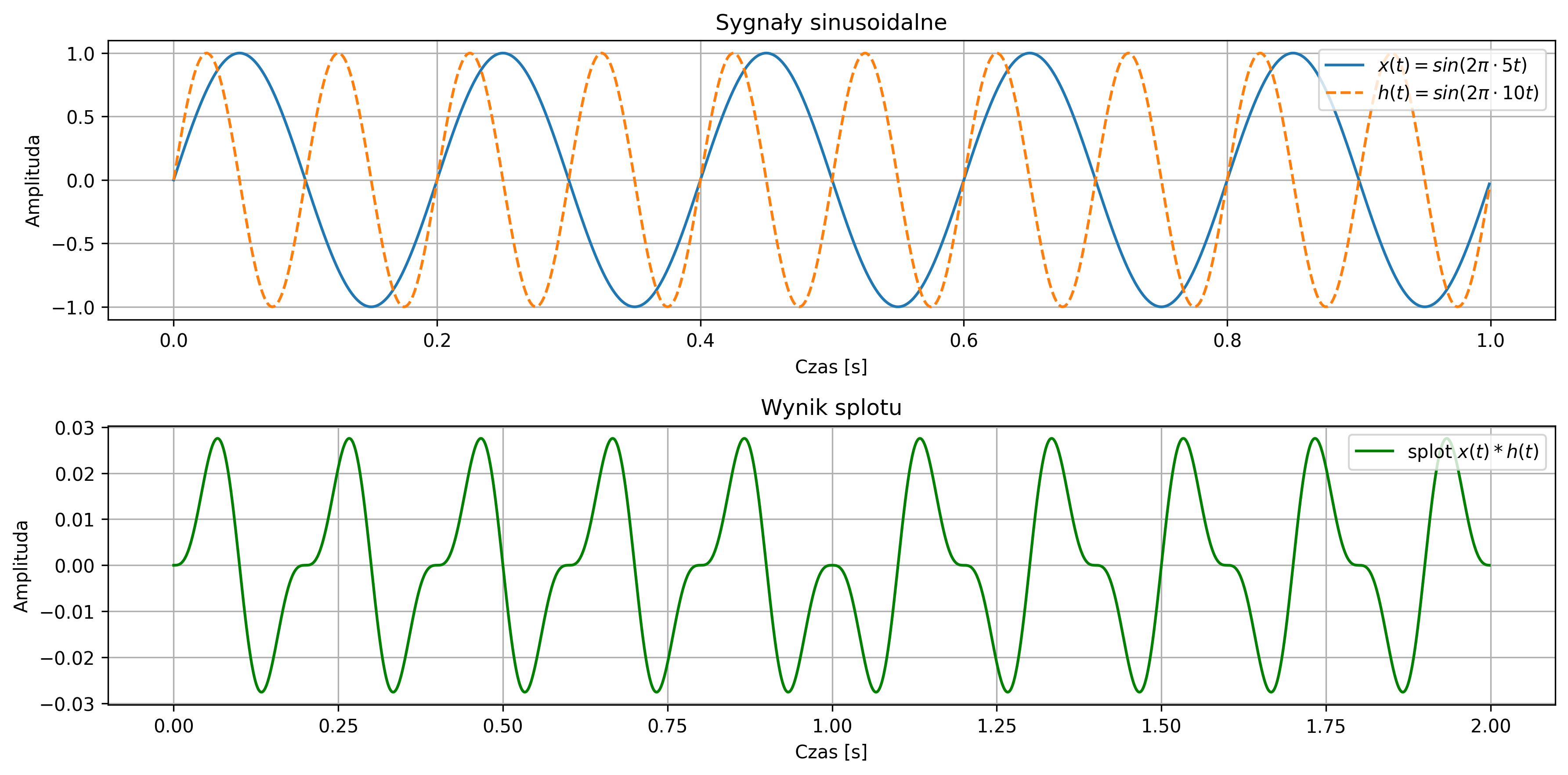
Wyznacz splot dwóch sygnałów sinusoidalnych o amplitudach \( A = 1 \), częstotliwościach \( 5 \) Hz i \( 10 \) Hz oraz zerowym przesunięciu fazowym. Narysować obydwa sygnały \( x(t)\) i \(h(t)\) oraz ich splot \(y(t)= x(t)\ast h(t)\).
 


import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import convolve

# Parametry
fs = 1000        # częstotliwość próbkowania [Hz]
T = 1 / fs       # okres próbkowania
t = np.arange(0, 1, T)  # oś czasu dla 1 sekundy

# Częstotliwości sygnałów
f1 = 5           # Hz
f2 = 10          # Hz

x = np.sin(2 * np.pi * f1 * t)       
h = np.sin(2 * np.pi * f2 * t)       

# Splot dyskretny
y = convolve(x, h, mode='full') * T
t_conv = np.arange(0, len(y)) * T    # oś czasu dla splotu

# Wykresy
plt.figure(figsize=(12, 6))

# Wykres 1: oba sygnały wejściowe
plt.subplot(2, 1, 1)
plt.plot(t, x, label=r'$x(t) = sin(2\pi \cdot 5t)$')
plt.plot(t, h, label=r'$h(t) = sin(2\pi \cdot 10t)$', linestyle='--')
plt.title('Sygnały sinusoidalne')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend(loc='upper right')

# Wykres 2: wynik splotu
plt.subplot(2, 1, 2)
plt.plot(t_conv, y, label=r'splot $x(t) * h(t)$', color='green')
plt.title('Wynik splotu')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend(loc='upper right')

plt.tight_layout()
plt.show()
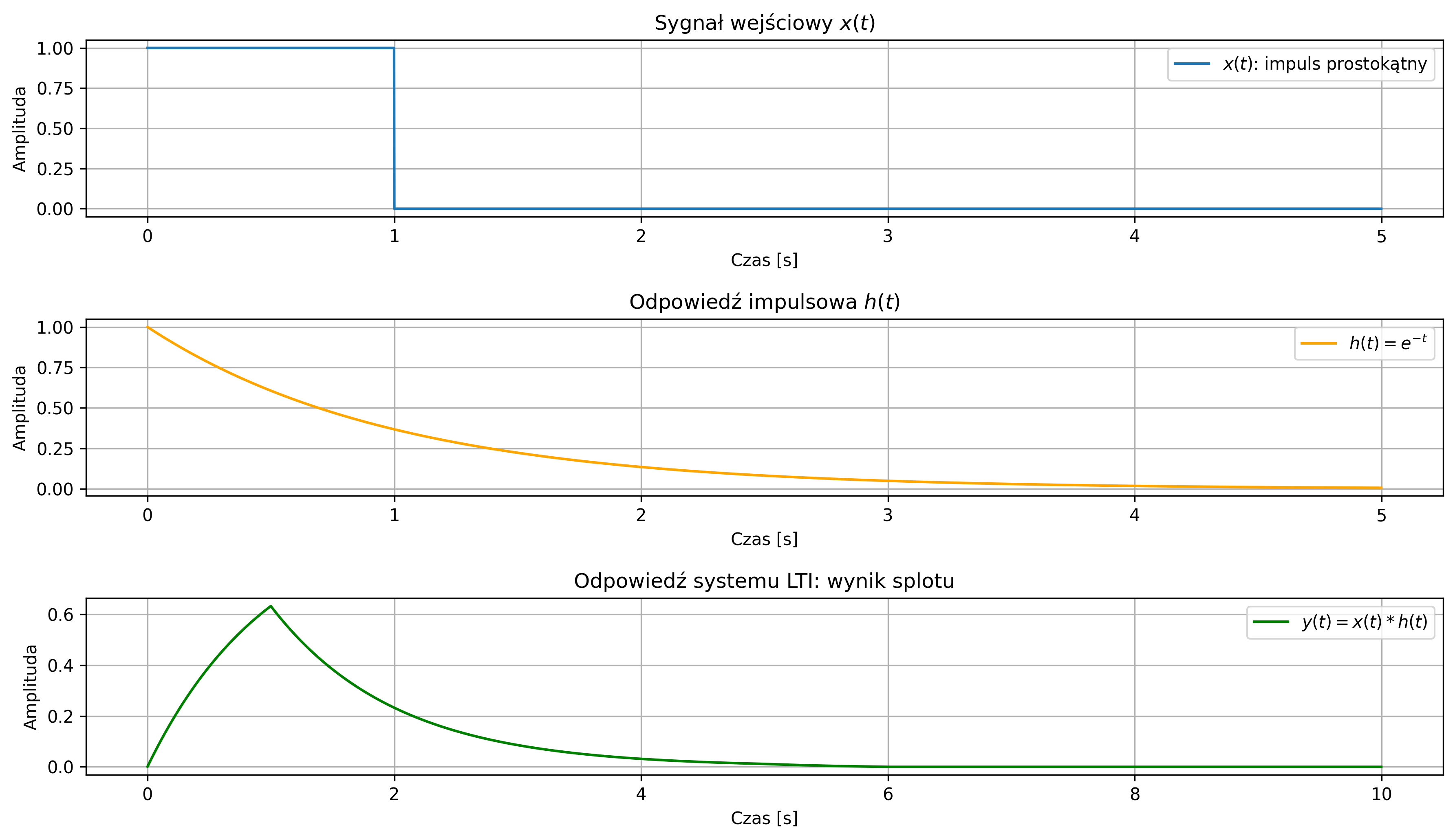
Zauważmy, że splot dwóch sygnałów sinusoidalnych o różnych częstotliwościach nie daje w rezultacie sygnału sinusoidalnego. Wynikiem jest fala o modulowanym kształcie, której amplituda zmienia się w czasie w zależności od wzajemnych częstotliwości i faz obu sygnałów. Wynik splotu zależy również od długości sygnałów oraz przyjętego okna czasowego, co należy uwzględnić przy analizie w dziedzinie czasu.

Wyznaczyć odpowiedź systemu LTI na sygnał wejściowy – impuls prostokątny, trwający \( 1 \) s, jeśli odpowiedź impulsowa systemu jest sygnałem wykładniczym malejącym:

\( h(t) = e^{-t}. \)

Przypomnijmy, że odpowiedź systemu LTI na dowolny sygnał wejściowy jest splotem sygnału wejściowego z odpowiedzią impulsową.


import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import convolve

# Parametry
fs = 1000          # częstotliwość próbkowania
T = 1 / fs         # okres próbkowania
t = np.arange(0, 5, T)  # od 0 do 5 s

# Sygnał wejściowy: impuls prostokątny trwający 1 [s]
x = np.where(t < 1, 1, 0)

# Odpowiedź impulsowa: sygnał wykładniczy malejąca
h = np.exp(-t)

# Splot
y = convolve(x, h, mode='full') * T
t_conv = np.arange(0, len(y)) * T 

# Wykresy
plt.figure(figsize=(12, 7))

plt.subplot(3, 1, 1)
plt.plot(t, x, label=r'$x(t)$: impuls prostokątny')
plt.title(r'Sygnał wejściowy $x(t)$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend()

plt.subplot(3, 1, 2)
plt.plot(t, h, label=r'$h(t) = e^{-t}$', color='orange')
plt.title(r'Odpowiedź impulsowa $h(t)$')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend()

plt.subplot(3, 1, 3)
plt.plot(t_conv, y, label=r'$y(t) = x(t) * h(t)$', color='green')
plt.title('Odpowiedź systemu LTI: wynik splotu')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend()

plt.tight_layout()
plt.show()