Podręcznik
2. Sygnały i ich charakterystyki
2.6. Korelacja wzajemna i autokorelacja
Kolejnym, alternatywnym sposobem charakteryzowania sygnałów w dziedzinie czasu jest opis korelacyjny. W przetwarzaniu sygnałów, korelacja wzajemna (ang. Cross-Correlation) jest miarą podobieństwa dwóch sygnałów.
Funkcja korelacji wzajemnej rzeczywistych sygnałów o ograniczonej energii to iloczyn skalarny dwóch sygnałów w funkcji przesunięcia jednego z nich i wyraża się wzorem:
gdzie:
- \( x(t) \) – pierwszy sygnał,
- \( y(t-\tau) \) – drugi sygnał przesunięty, ale nie odwrócony w czasie,
- \( \tau \) – przesunięcie.
Analogicznie definiuje się funkcję korelacji wzajemnej między sygnałem \( y(t) \) a sygnałem \( x(t) \):
W funkcji korelacji, drugi sygnał opóźnia się w stosunku do pierwszego o czas \( \tau \), następnie oba sygnały wymnaża się przez siebie i całkuje ich iloczyn. W ten sposób dla każdego przesunięcia \( \tau \) otrzymuje się wartość, która określa na ile opóźniony drugi sygnał jest podobny do sygnału pierwszego. Jest to operacja bardzo podobna do splotu, gdyż mierzy jak bardzo dwa sygnały są do siebie podobne, gdy jeden z nich jest przesuwany w czasie względem drugiego. Jednakże, w przeciwieństwie do operacji splotu, obliczając korelację nie odwracamy w czasie jednego z sygnałów.
Można pokazać, że
co oznacza, że taką samą wartość iloczynu skalarnego otrzymujemy przy przesunięciu sygnału \( y(t) \) w kierunku opóźnienia o czas \( \tau \), jak i przy przesunięciu sygnału \( x(t) \) o ten sam czas w kierunku przyspieszenia.
Funkcja korelacji wzajemnej dla dyskretnych sygnałów \( x \) i \( y \) przyjmuje postać:
Korelacja wzajemna pozwala wykrywać opóźnienia sygnałów względem siebie – położenie maksimum funkcji korelacji wskazuje na przesunięcie, które daje największe podobieństwo sygnałów.
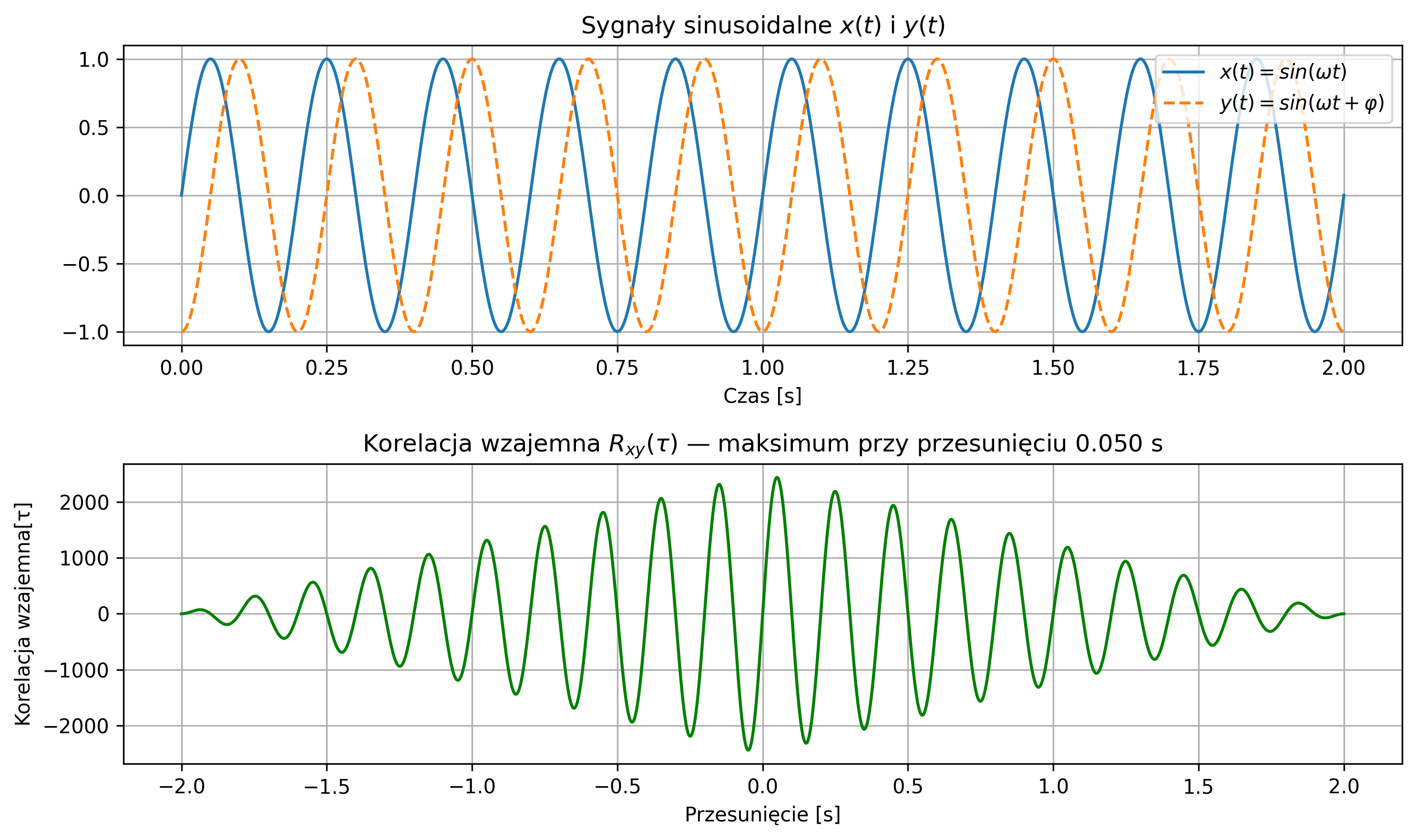
Na rys. 2.10 zostało pokazane wykorzystanie funkcji korelacji wzajemnej do wykrycia przesunięcia jednej sinusoidy:
względem drugiej \( y(t)=\sin(\omega t) \). Wykres korelacji wzajemnej pokazuje maksimum przy opóźnieniu \( \tau \), które wyniosło \( 0.25 \) s (\( \varphi=-7.85 \)).
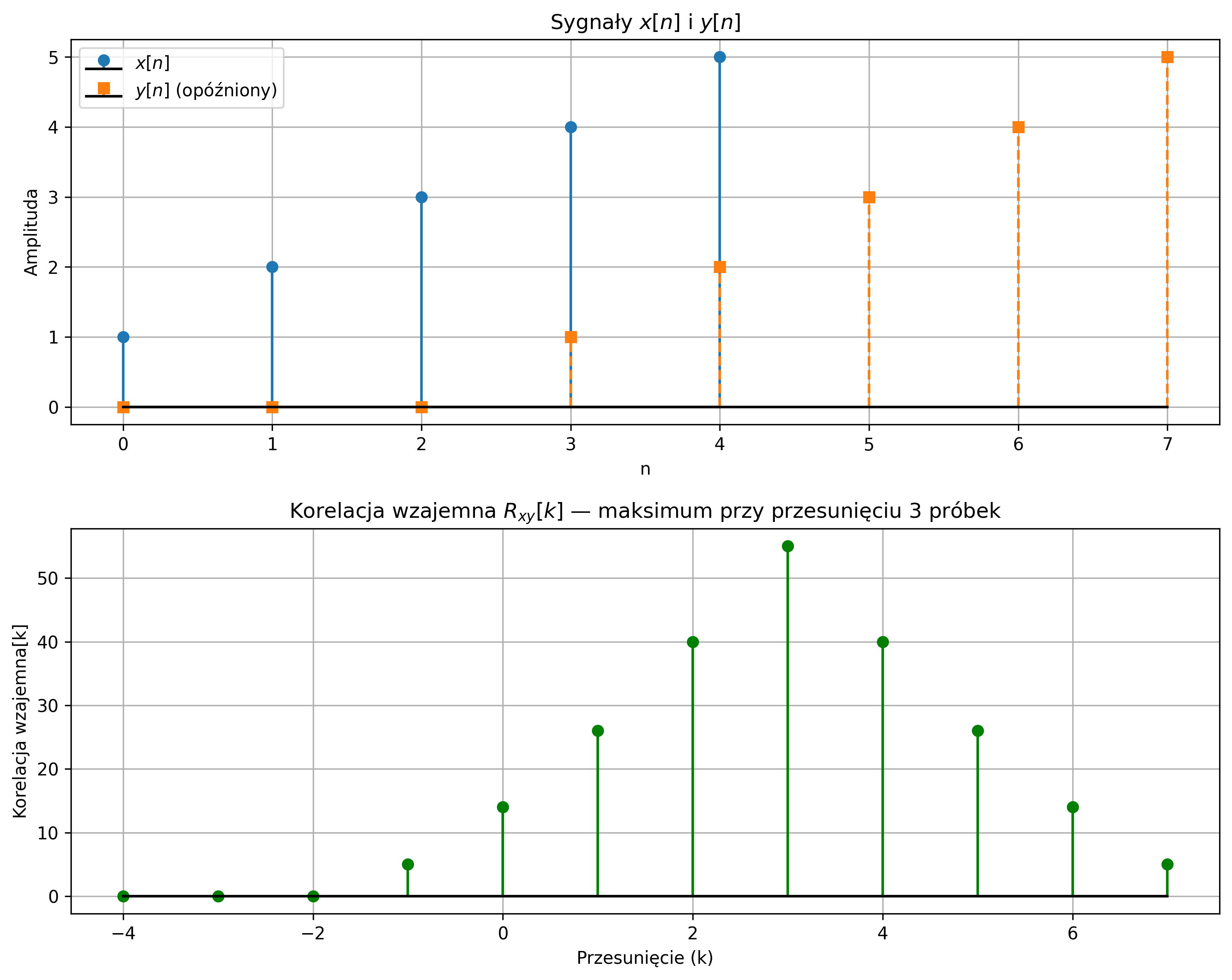
Analogiczny przykład, w wersji dyskretnych sygnałów został przedstawiony na rys. 2.11. Pokazany został przebieg ciągu próbek sygnału \( x = [1,2,3,4,5] \) oraz sygnału \( y \), który jest opóźnionym sygnałem \( x \) o 3 próbki. Korzystając z funkcji korelacji wzajemnej, wykryte zostało opóźnienie jednego sygnału względem drugiego – funkcja korelacji wzajemnej pokazała maksimum przy tym przesunięciu.
Szczególnym przypadkiem korelacji wzajemnej, gdy sygnał jest porównywany sam ze sobą, jest autokorelacja (ang. Autocorrelation). Autokorelacja dla danej wartości przesunięcia opisuje podobieństwo sygnału do jego przesuniętej w czasie kopii. Największe podobieństwo uzyskamy dla zerowego przesunięcia, gdy oba korelowane sygnały są identyczne.
Funkcja autokorelacji dla rzeczywistych sygnałów o ograniczonej energii:
gdzie:
- \( x(t) \) – pierwszy sygnał,
- \( x(t-\tau) \) – ten sam sygnał przesunięty, ale nie odwrócony w czasie,
- \( \tau \) – przesunięcie,
jest rzeczywista i parzysta – nie ma znaczenia, w którą stronę przesuwamy kopię sygnału: \( R_{xx}(\tau)=R_{xx}(-\tau) \).
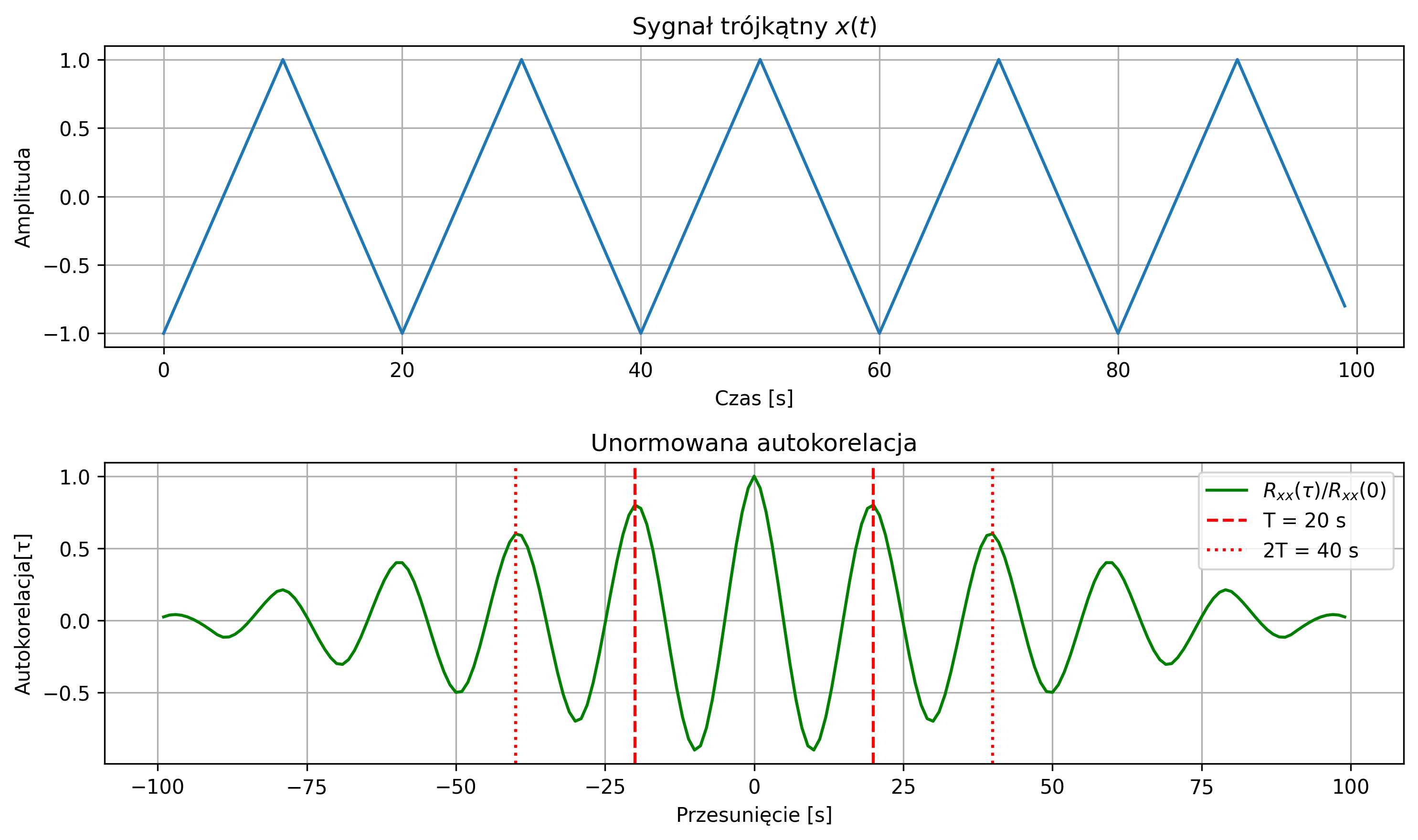
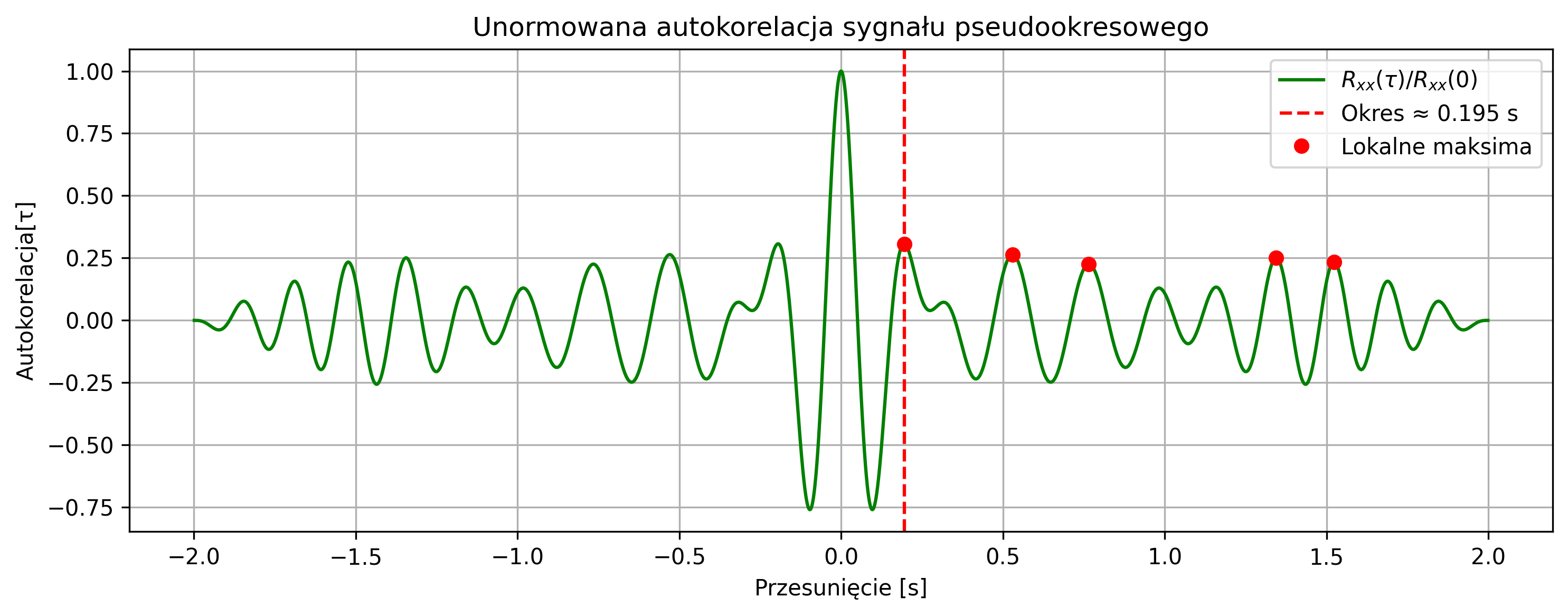
Autokorelacja jest przede wszystkim wykorzystywana do badania okresowości sygnału, ponieważ przyjmuje ona wartości maksymalne dla wartości przesunięcia \( \tau \) równego wielokrotności okresu sygnału. Może również posłużyć do wykrywania pewnych regularności w sygnałach – np. regularnych cykli tętna w przebiegu fal EEG.
Funkcja autokorelacji sygnału o ograniczonej energii jest także funkcją o ograniczonej energii. Zauważmy, że wartość funkcji autokorelacji w punkcie \( \tau = 0 \) jest równa energii sygnału:
Unormowana funkcja autokorelacji powstaje przez podzielenie wartości funkcji autokorelacji przez energię sygnału. Wtedy, dla zerowego przesunięcia, wartość autokorelacji przyjmuje wartość maksymalną, równą \(1\). Dzięki temu można porównywać kształt funkcji autokorelacji różnych sygnałów niezależnie od ich amplitudy i energii.
Na rys. 2.12 przedstawiono wykres sygnału trójkątnego i jego unormowanej funkcji autokorelacji. Ponieważ sygnał jest okresowy, maksima funkcji autokorelacji znajdują się w punktach równych wielokrotności okresu.