Podręcznik

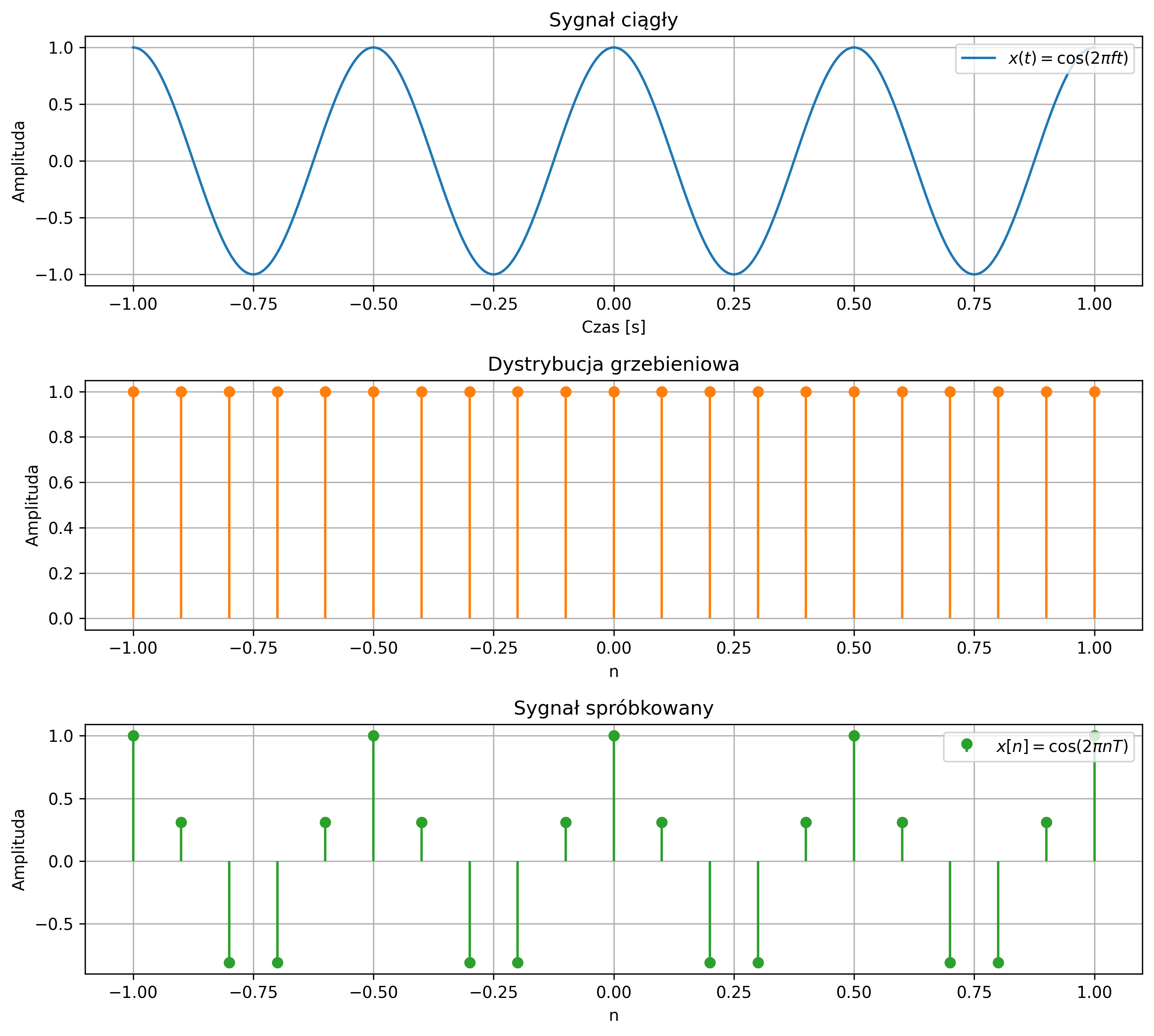
Próbkowanie to proces przekształcania sygnału ciągłego w sygnał dyskretny poprzez pobieranie jego wartości w równych odstępach czasu. Stanowi ono pierwszy etap konwersji analogowo-cyfrowej (A/C) i jest niezbędne do analizy oraz przetwarzania sygnałów w systemach cyfrowych. W przypadku próbkowania w regularnych odstępach czasu podaje się częstotliwość próbkowania, wyrażaną w liczbie próbek na sekundę, czyli w hercach (Hz). Dla próbkowania wielowymiarowego określa się rozdzielczość w postaci liczby punktów lub pikseli na cal. Obecnie produkowane przetworniki analogowo-cyfrowe oferują maksymalną częstotliwość próbkowania od kilkudziesięciu kiloherców do kilku megaherców.

W wyniku próbkowania równomiernego z okresem $T$ sygnał analogowy $x(t)$ jest przetworzony w sygnał dyskretny $x[n]$, którego argumentem jest czas unormowany względem okresu próbkowania. Proces próbkowania można stosunkowo łatwo modyfikować poprzez zmianę okresu próbkowania. Należy jednak pamiętać, że wpływa to na odwzorowanie sygnału analogowego w zapisie cyfrowym oraz ma istotne znaczenie dla identyfikacji i przetwarzania sygnału.

W rozdziale 2.4 została opisana operacja splotu i jej podstawowa własność – elementem identycznościowym operacji splotu jest impuls Diraca:

$x(t)\ast \delta(t) = x(t)$ oraz $x(t)\ast \delta(t-t_0) = x(t-t_0)$

Matematycznie proces próbkowania można opisać jako mnożenie sygnału ciągłego przez funkcję impulsów jednostkowych Diraca rozmieszczonych okresowo – dystrybucję grzebieniową.

Dystrybucja grzebieniowa jest okresowym ciągiem impulsów Diraca, powtarzanych z okresem $T$. Jej wykres przypomina nieskończony grzebień, którego „zęby” są równoodległe i mają jednakową wysokość: