3. Cyfrowe przetwarzanie sygnałów

3.3. Próbkowanie sygnałów w języku Python

Celem poniższych ćwiczeń jest zapoznanie się z podstawowymi poleceniami języka Python, które umożliwiają poprawne próbkowanie sygnałów ciągłych oraz generowanie ich przebiegów czasowych.

Poniższe przykłady przedstawiają pełne kody źródłowe w języku Python, opracowane na potrzeby realizacji poszczególnych zadań. Do wykonania przedstawionych zadań wymagane jest wykorzystanie następujących bibliotek języka Python:


import numpy as np                # obliczenia numeryczne i tablice
import matplotlib.pyplot as plt   # tworzenie wykresów ciągłych i dyskretnych
import scipy.signal as signal     # generowanie standardowych sygnałów,                              
                                  # takich jak np. prostokątny, trójkątny, piłokształtny 

oraz wymagana jest znajomość między innymi funkcji:


sawtooth    # generowanie sygnału piłokształtnego (scipy.signal)
np.interp   # interpolacja liniowa jednowymiarowych danych (NumPy)

Do rekonstrukcji sygnałów wykorzystano metodę interpolacji Sinc, będącą jedną z najdokładniejszych metod rekonstrukcji w teorii cyfrowego przetwarzania sygnałów. W poniższych implementacjach została ona zdefiniowana w postaci funkcji:


 sinc_interp()

Poniżej znajdują się ćwiczenia z przykładową implementacją. Autor zachęca czytelnika do realizacji poniższych kodów oraz do analizy różnych parametrów próbkowania sygnałów, poprzez ich modyfikację.

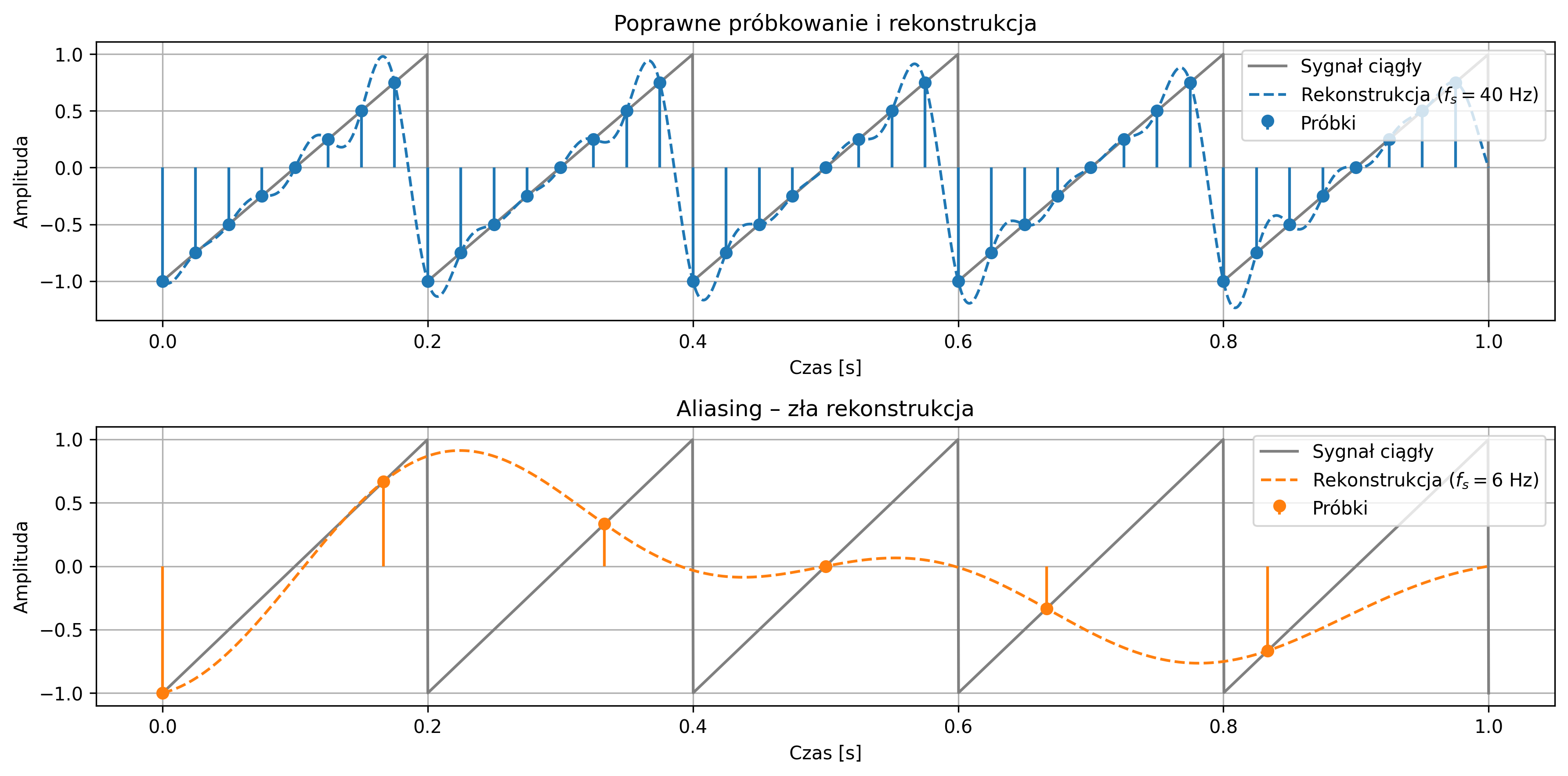
Z wykorzystaniem interpolacji, dokonać rekonstrukcji ciągłego sygnału piłokształtnego o częstotliwości \(5\) Hz i o czasie trwania \(1\) s. Przyjąć dwie częstotliwości próbkowania: \(40\) Hz i \(6\) Hz.


import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import sawtooth

# Parametry
f = 5            # częstotliwość sygnału [Hz]
T = 1            # czas obserwacji [s]
t_cont = np.linspace(0, T, 2000)  # czas ciągły

# Sygnał piłokształtny
x_cont = sawtooth(2 * np.pi * f * t_cont)

# Próbkowanie
fs_good = 40
fs_bad = 6

t_good = np.arange(0, T, 1/fs_good)
x_good = sawtooth(2 * np.pi * f * t_good)

t_bad = np.arange(0, T, 1/fs_bad)
x_bad = sawtooth(2 * np.pi * f * t_bad)

# Rekonstrukcja przez interpolację sinc
def sinc_interp(x, t, t_new):
    T = t[1] - t[0]
    sinc_matrix = np.sinc((t_new[:, None] - t[None, :]) / T)
    return np.dot(sinc_matrix, x)

x_rec_good = sinc_interp(x_good, t_good, t_cont)
x_rec_bad = sinc_interp(x_bad, t_bad, t_cont)

# Wykresy
fig, axs = plt.subplots(2, 1, figsize=(12, 6), sharex=False)

# Poprawna rekonstrukcja
axs[0].plot(t_cont, x_cont, color='gray', label='Sygnał ciągły')
axs[0].plot(t_cont, x_rec_good, 'C0--', label=rf"Rekonstrukcja ($f_s = {fs_good}$ Hz)")
axs[0].stem(t_good, x_good, linefmt='C0-', markerfmt='C0o', basefmt=" ", label='Próbki')
axs[0].set_title('Poprawne próbkowanie i rekonstrukcja')
axs[0].set_xlabel('Czas [s]')
axs[0].legend(loc='upper right')
axs[0].set_ylabel('Amplituda')
axs[0].grid(True)

# Błędna rekonstrukcja (aliasing)
axs[1].plot(t_cont, x_cont, color='gray', label='Sygnał ciągły')
axs[1].plot(t_cont, x_rec_bad, 'C1--', label=rf"Rekonstrukcja ($f_s = {fs_bad}$ Hz)")
axs[1].stem(t_bad, x_bad, linefmt='C1-', markerfmt='C1o', basefmt=" ", label='Próbki')
axs[1].set_title('Aliasing – zła rekonstrukcja')
axs[1].set_xlabel('Czas [s]')
axs[1].set_ylabel('Amplituda')
axs[1].legend()
axs[1].grid(True)

plt.tight_layout()
plt.show()
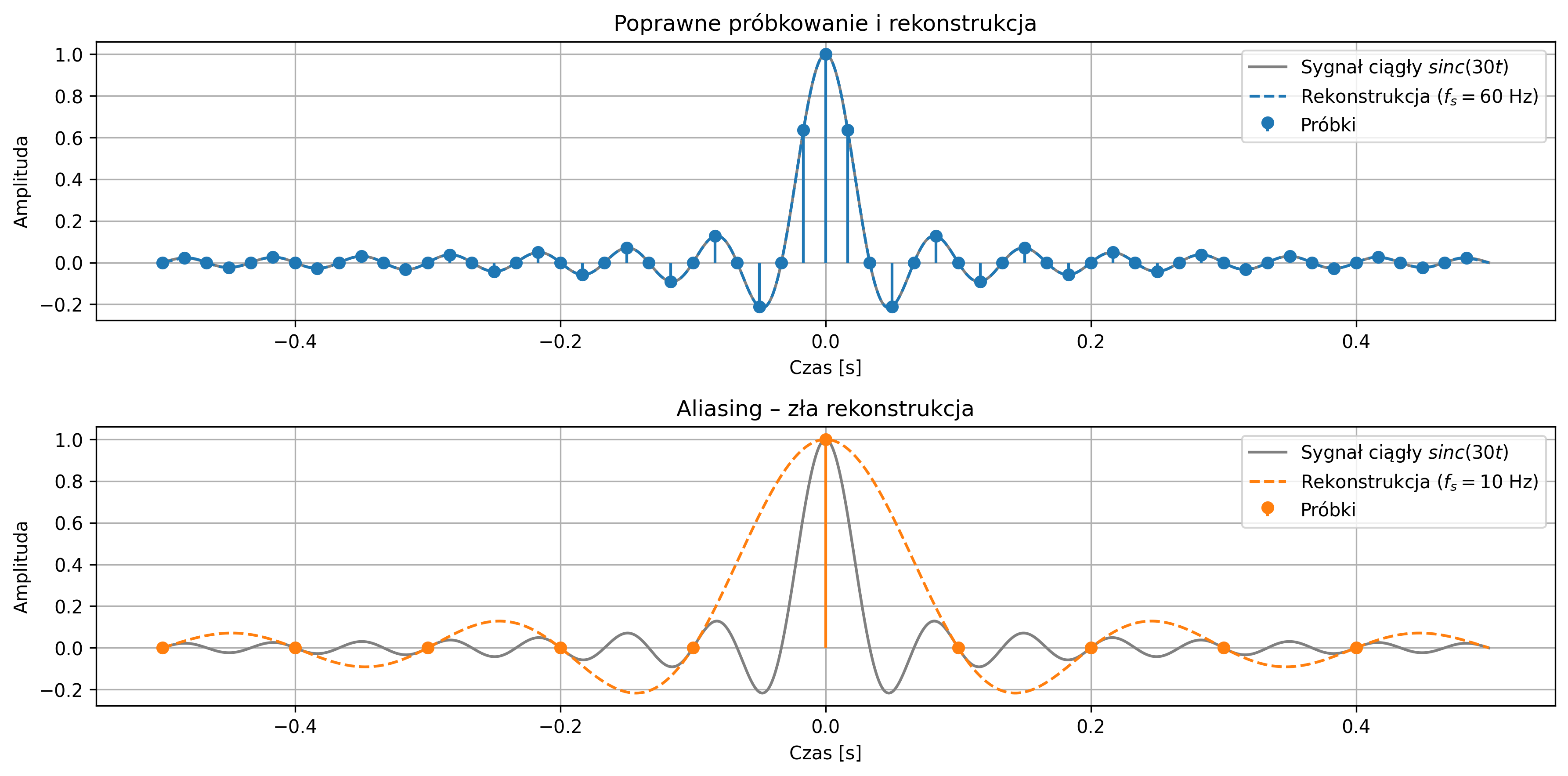
Na górnym wykresie został przedstawiony poprawny proces próbkowania – próbki zostały pobrane z częstotliwością \(40\) Hz, czyli dużo powyżej dwukrotności częstotliwości sygnału. Sygnał został zrekonstruowany poprawnie – odwzorowuje przebieg piłokształtny. Na dolnym wykresie zostało pokazane zjawisko aliasingu i błędnej rekonstrukcji sygnału. Próbki zostały pobrane z częstotliwością \(6\) Hz, czyli dużo poniżej progu Nyquista. Otrzymane próbki sugerują inny kształt - rekonstrukcja nie przypomina sygnału oryginalnego.

Z wykorzystaniem interpolacji, dokonać rekonstrukcji ciągłego sygnału \(\mathrm{Sinc}(30t)\) o czasie trwania \(1\) s. Przyjąć dwie częstotliwości próbkowania: \(60\) Hz i \(10\) Hz.


import numpy as np
import matplotlib.pyplot as plt

# Parametry
T = 1                                   # czas obserwacji [s]
t_cont = np.linspace(-T/2, T/2, 2000)   # czas ciągły
x_cont = np.sinc(30 * t_cont)    

# Próbkowanie
fs_good = 60
fs_bad = 10

# Sygnał sinc
t_good = np.arange(-T/2, T/2, 1/fs_good)
x_good = np.sinc(30 * t_good)

t_bad = np.arange(-T/2, T/2, 1/fs_bad)
x_bad = np.sinc(30 * t_bad)

# Interpolacja sinc
def sinc_interp(x, t, t_new):
    T = t[1] - t[0]
    return np.dot(np.sinc((t_new[:, None] - t[None, :]) / T), x)

x_rec_good = sinc_interp(x_good, t_good, t_cont)
x_rec_bad = sinc_interp(x_bad, t_bad, t_cont)

# Wykresy
fig, axs = plt.subplots(2, 1, figsize=(12, 6), sharex=False)

# Poprawna rekonstrukcja
axs[0].plot(t_cont, x_cont, color='gray', label=rf'Sygnał ciągły $sinc(30t)$')
axs[0].plot(t_cont, x_rec_good, 'C0--', label=rf'Rekonstrukcja ($f_s = {fs_good}$ Hz)')
axs[0].stem(t_good, x_good, linefmt='C0-', markerfmt='C0o', basefmt=" ", label='Próbki')
axs[0].set_title('Poprawne próbkowanie i rekonstrukcja')
axs[0].set_xlabel('Czas [s]')
axs[0].legend(loc='upper right')
axs[0].set_ylabel('Amplituda')
axs[0].grid(True)

# Błędna rekonstrukcja (aliasing)
axs[1].plot(t_cont, x_cont, color='gray', label=rf'Sygnał ciągły $sinc(30t)$')
axs[1].plot(t_cont, x_rec_bad, 'C1--', label=rf'Rekonstrukcja ($f_s = {fs_bad}$ Hz)')
axs[1].stem(t_bad, x_bad, linefmt='C1-', markerfmt='C1o', basefmt=" ", label='Próbki')
axs[1].set_title('Aliasing – zła rekonstrukcja')
axs[1].set_xlabel('Czas [s]')
axs[1].set_ylabel('Amplituda')
axs[1].legend()
axs[1].grid(True)

plt.tight_layout()
plt.show()

Z wykorzystaniem interpolacji, dokonać rekonstrukcji ciągłego sygnału:

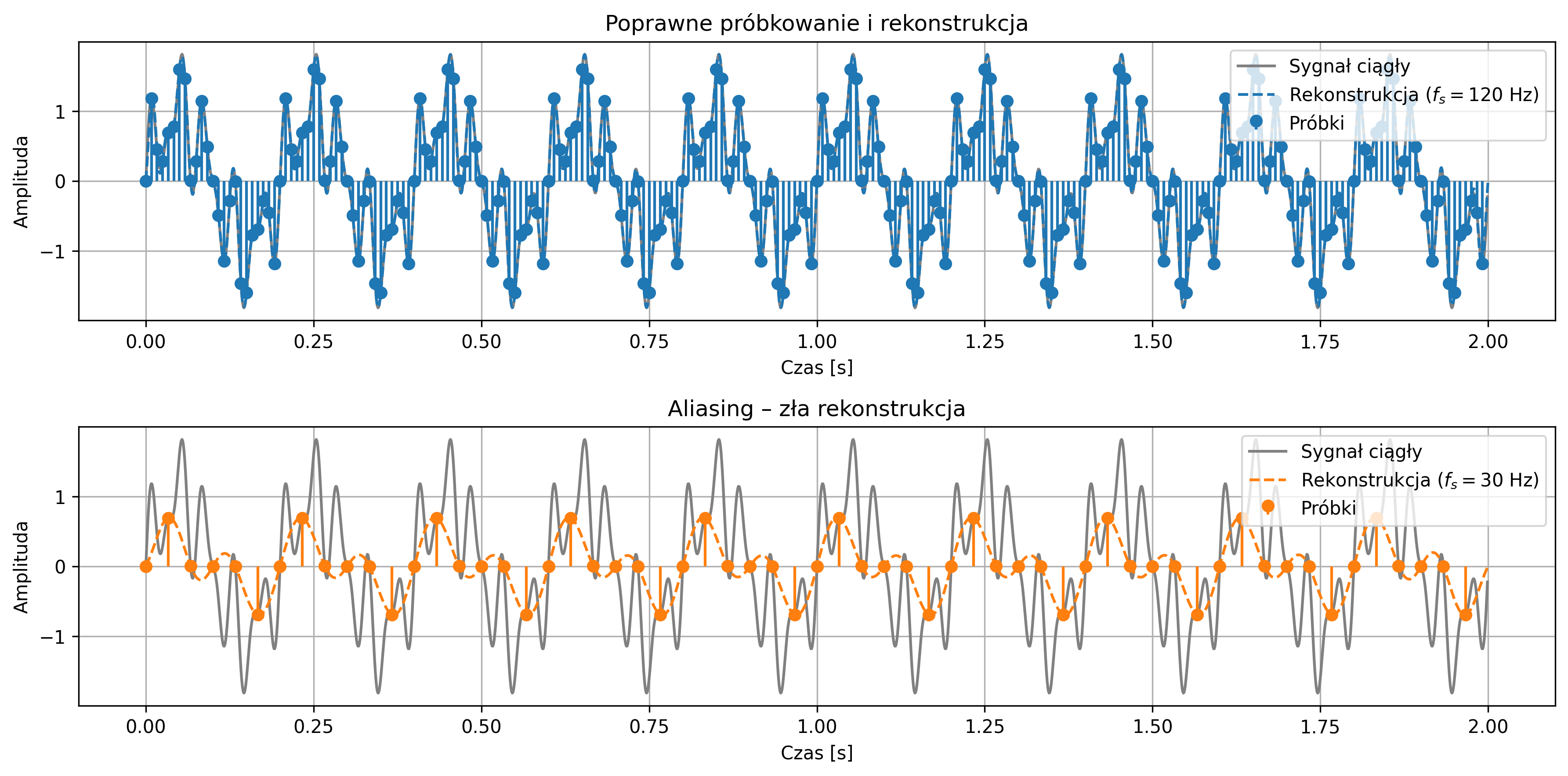
\( x(t)=\sin(2\pi\cdot 5t)+0.6\sin(2\pi\cdot 25t)+0.4\sin(2\pi\cdot 40t) \).

Przyjąć dwie częstotliwości próbkowania: \(120\) Hz i \(30\) Hz.


 import numpy as np
import matplotlib.pyplot as plt

# Sygnał: suma sinusów (5 Hz + 25 Hz + 40 Hz)
def sum_signal(t):
    return (
        np.sin(2 * np.pi * 5 * t) +         # niska
        0.6 * np.sin(2 * np.pi * 25 * t) +  # średnia
        0.4 * np.sin(2 * np.pi * 40 * t)    # wysoka (aliasowana!)
    )

# Parametry
T = 2                                  # czas obserwacji [s]   
t_cont = np.linspace(0, T, int(1000 * T), endpoint=False)   # czas ciągły
x_cont = sum_signal(t_cont)

# Interpolacja sinc
def sinc_interp(x, t, t_new):
    T = t[1] - t[0]
    return np.dot(np.sinc((t_new[:, None] - t[None, :]) / T), x)

# Próbkowanie
fs_good = 120  
fs_bad = 30   

# Sygnały
t_good = np.arange(0, T, 1/fs_good)
x_good = np.interp(t_good, t_cont, x_cont)  # do symulacju próbkowania

t_bad = np.arange(0, T, 1/fs_bad)
x_bad = np.interp(t_bad, t_cont, x_cont) # do symulacju próbkowania

t_dense = np.linspace(0, T, 5000)
x_rec_good = sinc_interp(x_good, t_good, t_dense)
x_rec_bad = sinc_interp(x_bad, t_bad, t_dense)

# Wykresy
fig, axs = plt.subplots(2, 1, figsize=(12, 6), sharex=False)

# Poprawna rekonstrukcja
axs[0].plot(t_cont, x_cont, color='gray', label=rf'Sygnał ciągły')
axs[0].plot(t_dense, x_rec_good, 'C0--', label=rf'Rekonstrukcja ($f_s = {fs_good}$ Hz)')
axs[0].stem(t_good, x_good, linefmt='C0-', markerfmt='C0o', basefmt=" ", label='Próbki')
axs[0].set_title('Poprawne próbkowanie i rekonstrukcja')
axs[0].set_xlabel('Czas [s]')
axs[0].legend(loc='upper right')
axs[0].set_ylabel('Amplituda')
axs[0].grid(True)

# Błędna rekonstrukcja (aliasing)
axs[1].plot(t_cont, x_cont, color='gray', label=rf'Sygnał ciągły')
axs[1].plot(t_dense, x_rec_bad, 'C1--', label=rf'Rekonstrukcja ($f_s = {fs_bad}$ Hz)')
axs[1].stem(t_bad, x_bad, linefmt='C1-', markerfmt='C1o', basefmt=" ", label='Próbki')
axs[1].set_title('Aliasing – zła rekonstrukcja')
axs[1].set_xlabel('Czas [s]')
axs[1].set_ylabel('Amplituda')
axs[1].legend()
axs[1].grid(True)

plt.tight_layout()
plt.show()
Sygnał ciągły jest złożeniem sinusoidy o niskiej częstotliwości (\(5\) Hz), sinusoidy o średniej częstotliwości (\(25\) Hz) i sinusoidy o wysokiej częstotliwości (\(40\) Hz). Ostatnia składowa sygnału powoduje aliasing, gdyż częstotliwość próbkowania (\(30\) Hz) jest poniżej \( 2\cdot 40 = 80 \) Hz.