Podręcznik
4. Analiza częstotliwościowa sygnałów
4.1. Szereg Fouriera
Jean-Baptiste Joseph Fourier odkrył, że dowolny sygnał okresowy (spełniający pewne warunki matematyczne) można przedstawić jako szereg Fouriera, czyli sumę funkcji trygonometrycznych – sinusów i cosinusów – o różnych amplitudach, częstotliwościach i fazach. Oznacza to, że szeroka klasa sygnałów może być reprezentowana jako kombinacja liniowa sygnałów harmonicznych.
Sygnałami harmonicznymi nazywamy takie, które można rozłożyć na sumę sygnałów sinusoidalnych o częstotliwościach będących całkowitą wielokrotnością częstotliwości podstawowej – najniższej wspólnej częstotliwości, z którą wszystkie składowe harmoniczne są całkowitymi wielokrotnościami. Pierwsza z tych składowych to składowa podstawowa – jej częstotliwość odpowiada częstotliwości sygnału. Kolejne składowe to tzw. harmoniczne. Suma wszystkich tych składowych tworzy szereg harmoniczny.
Jeśli sygnał \(x(t)\) jest okresowy z okresem \(T_0\), ma skończoną energię, to jego szereg Fouriera ma postać:
gdzie:
- \( f_0 = \dfrac{1}{T_0} \) – częstotliwość podstawowa sygnału,
- \( \omega_0 \) – pulsacja podstawowa,
- \( a_k \) i \( b_k \) – współczynniki Fouriera,
- \( k \) – numer kolejnej harmonicznej.
Istotną rolę odgrywają tzw. warunki Dirichleta, które stanowią zestaw wystarczających, choć nie koniecznych, kryteriów gwarantujących istnienie rozwinięcia Fouriera oraz jego zbieżność. Warunki te wymagają, aby w obrębie jednego okresu funkcja była całkowalna (posiadała skończoną energię), miała skończoną liczbę maksimów i minimów oraz skończoną liczbę punktów nieciągłości. Spełnienie tych warunków zapewnia, że szereg Fouriera będzie zbieżny. W kontekście sygnałów okresowych oznacza to, że większość sygnałów spotykanych w praktyce inżynierskiej, takich jak sygnały prostokątne, piłokształtne czy sygnały sinusoidalne, może być rozwijana w szeregi Fouriera. Jeśli sygnał nie spełnia warunków Dirichleta, nie wyklucza to całkowicie możliwości jego reprezentacji w postaci szeregu Fouriera, jednak analiza wymaga wtedy ujęcia bardziej ogólnego (np. w przestrzeni \(L^2\)).
Rozważmy rozwinięcie w szereg Fouriera sygnału prostokątnego o wartościach z przedziału \([-1,1]\) i okresie \(T = 2\pi\):
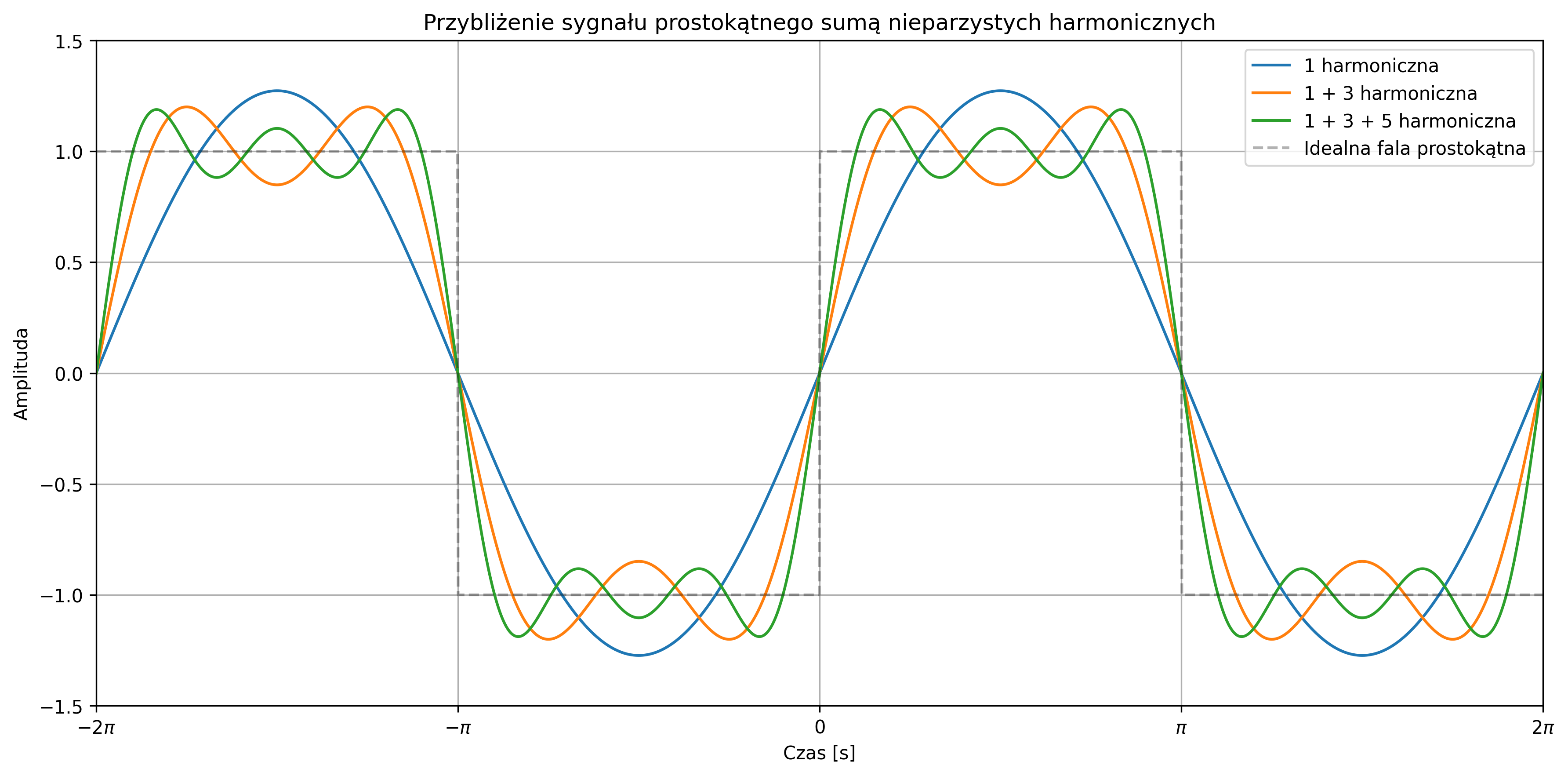
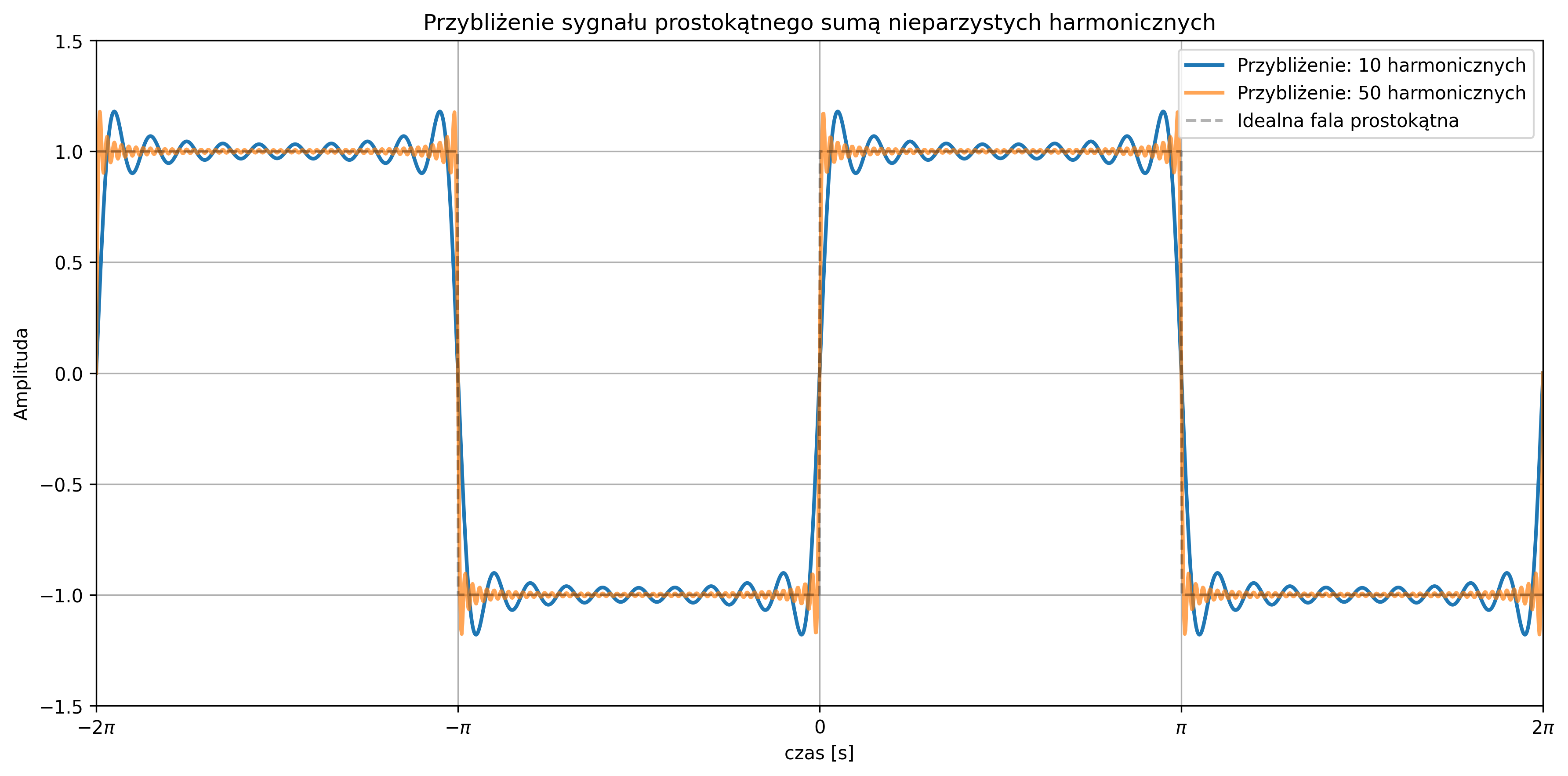
Zamiast używać osobno funkcji \(\sin\) i \(\cos\), można wprowadzić bardziej intuicyjną postać szeregu Fouriera, tzw. postać amplitudowo-fazową, w której każda harmoniczna reprezentowana jest przez jedną funkcję sinusoidalną o określonej amplitudzie \(A_k\) i fazie \(\varphi_k\):
gdzie:
- \( A_k = \sqrt{a_k^2 + b_k^2} \) – amplituda \(k\)-tej harmonicznej,
- \( \varphi_k = \operatorname{arctan}\!\big(-\dfrac{b_k}{a_k}\big) \) – przesunięcie fazowe.
Postać ta pozwala łatwiej wizualizować składniki sygnału w przestrzeni częstotliwości. Zbiór par:
gdzie \( f_k = k f_0 \), tworzy tzw. widmo amplitudowo-fazowe sygnału. Jest to reprezentacja, która pokazuje, jakie częstotliwości wchodzą w skład sygnału i z jakimi amplitudami oraz fazami.
Widmo to może być:
- widmem amplitudowym – przedstawia tylko amplitudy,
- widmem fazowym – pokazuje przesunięcia fazowe,
- pełnym widmem zespolonym.
Reprezentacja widma na wykresie:
- oś pozioma reprezentuje częstotliwość (w Hz) lub pulsację (w rad/s),
- oś pionowa:
- na widmie amplitudowym pokazuje amplitudy składowych harmonicznych – wysokość prążka jest proporcjonalna do wartości amplitudy,
- na widmie fazowym przedstawia przesunięcie fazowe (w rad) dla każdej częstotliwości obecnej w sygnale.
Do charakterystycznych cech widma sygnałów okresowych należą:
- widmo amplitudowe jest prążkowe – zawiera prążki w miejscach odpowiadających harmonicznym sygnału,
- odległość między prążkami wynosi \(\Delta f = \dfrac{1}{T}\) – im dłuższy okres, tym mniejsza odległość między składowymi,
- widmo amplitudowe sygnału rzeczywistego jest parzyste – symetryczne względem osi pionowej (częstotliwości 0),
- widmo fazowe sygnału rzeczywistego jest nieparzyste – symetryczne względem początku układu współrzędnych:
- w przypadku sygnału parzystego faza wynosi 0 lub \(\pi\),
- w przypadku sygnału nieparzystego faza może wynosić \(\pm \dfrac{\pi}{2}\).
Warto zaznaczyć, że:
- zerowe prążki w amplitudzie oznaczają brak danej częstotliwości w sygnale,
- skoki w fazie mogą wynikać z przejść przez 0 w widmie amplitudowym lub z natury sygnału (np. przesunięcia w czasie),
- dla sygnałów nieokresowych widmo staje się ciągłe, a nie prążkowe.
Na rys. 4.3 przedstawiono przykład widma amplitudowo-fazowego sygnału okresowego – sygnału prostokątnego. Prążki odpowiadają tylko nieparzystym harmonicznym, zgodnie z rozwinięciem w szereg Fouriera. Im wyższa harmoniczna, tym mniejsza jest amplituda \(A_k\). Na wykresie fazowym faza stała, równa \(-\dfrac{\pi}{2}\) dla wszystkich harmonicznych.
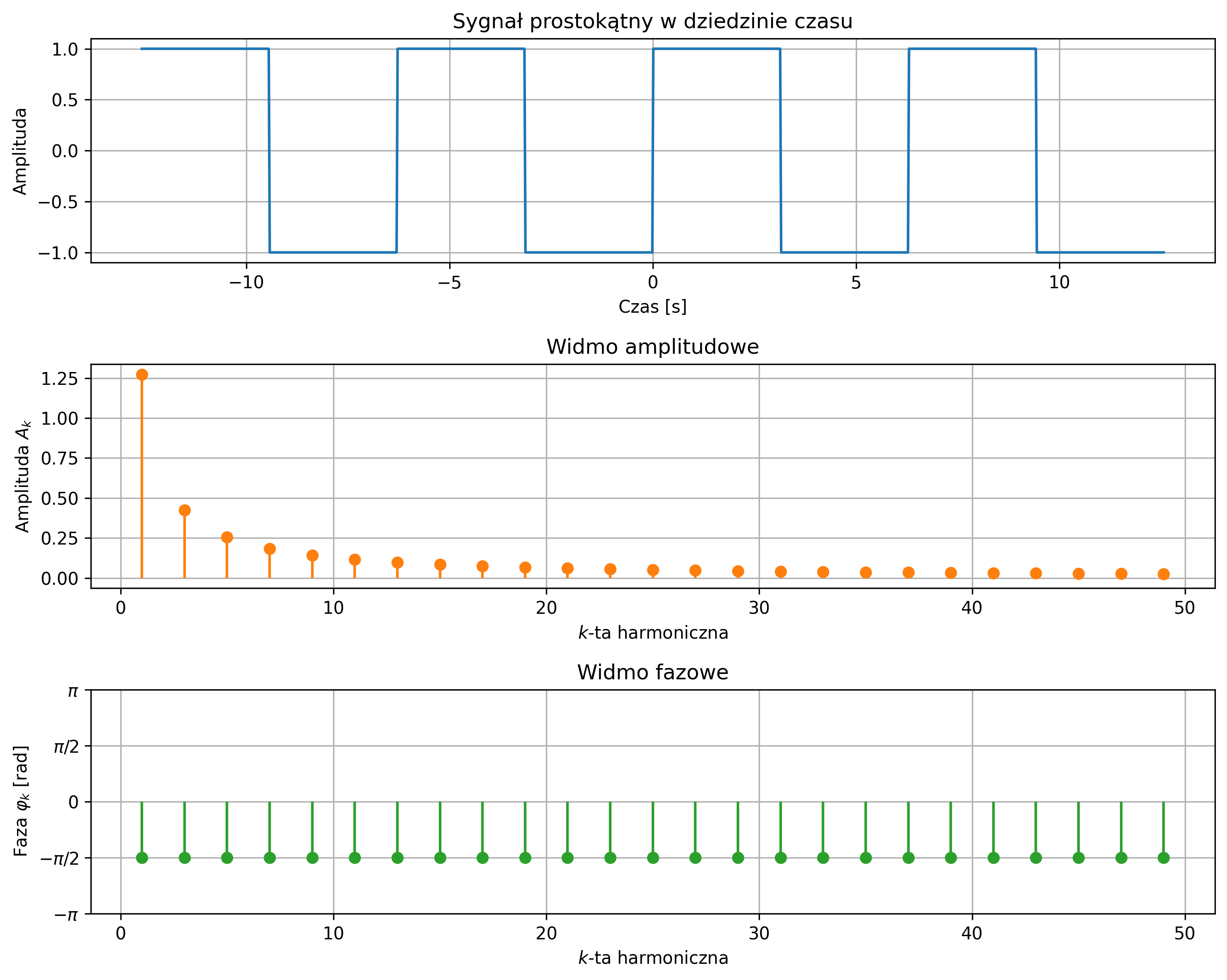
Równoważnie do postaci amplitudowo-fazowej, szereg Fouriera można przedstawić również w postaci tzw. wykładniczej:
gdzie:
- \( \omega_0 = \dfrac{2\pi}{T} \),
- współczynniki \(c_k\) są zespolone oraz opisują amplitudę i fazę poszczególnych harmonicznych.
Wtedy widmo amplitudowe sygnału to wykres wartości \(|c_k|\) w funkcji indeksu \(k\) lub częstotliwości \(f_k = k f_0\), zaś widmo fazowe to wykres argumentu (faz) współczynników. Wersja wykładnicza operuje na współczynnikach zespolonych \(c_k\), natomiast trygonometryczna na rzeczywistych \(a_k\) i \(b_k\).
Na wykresie rys. 4.4 przedstawiony jest przebieg trzech okresów sygnału piłokształtnego w dziedzinie czasu oraz widmo amplitudowe \(|c_k|\). Ponieważ jest to sygnał niesymetryczny, na wykresie amplitudowym znajdują się prążki zarówno dla parzystych, jak i nieparzystych harmonicznych.
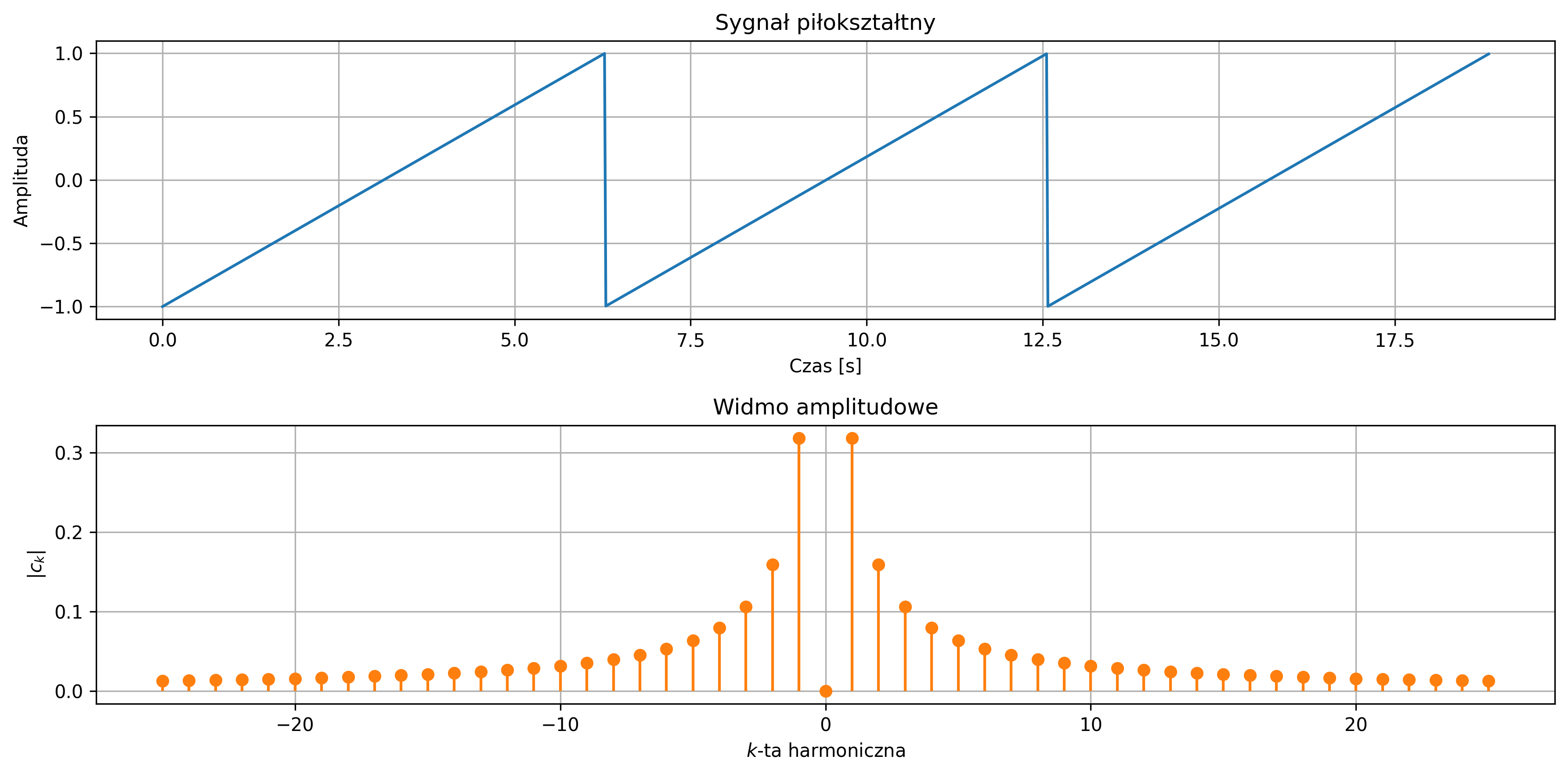
Dla szeregów Fouriera sygnałów okresowych spełnione jest równanie Parsevala:
Oznacza to, że średnia moc sygnału w czasie lub energia w jednym okresie podzielona przez długość okresu jest równa sumie kwadratów modułów współczynników Fouriera, czyli „mocy” poszczególnych harmonicznych.
Teoretyczna wartość energii dla sygnału okresowego piłokształtnego, który został przedstawiony na rys. 4.4, wynosi:
W rzeczywistości suma \(|c_k|^2\) wyniosła \(0.3254\), zaś energia \(0.3323\) – nieznaczne różnice w stosunku do wartości teoretycznej wynikają z przybliżonych obliczeń numerycznych. Należy zaznaczyć, że obliczenia energii są wykonywane tylko na jednym okresie, gdyż współczynniki Fouriera odnoszą się tylko do jednego pełnego okresu. Nie jest to energia całkowita, ponieważ całkowita energia sygnału okresowego wynosi nieskończoność.
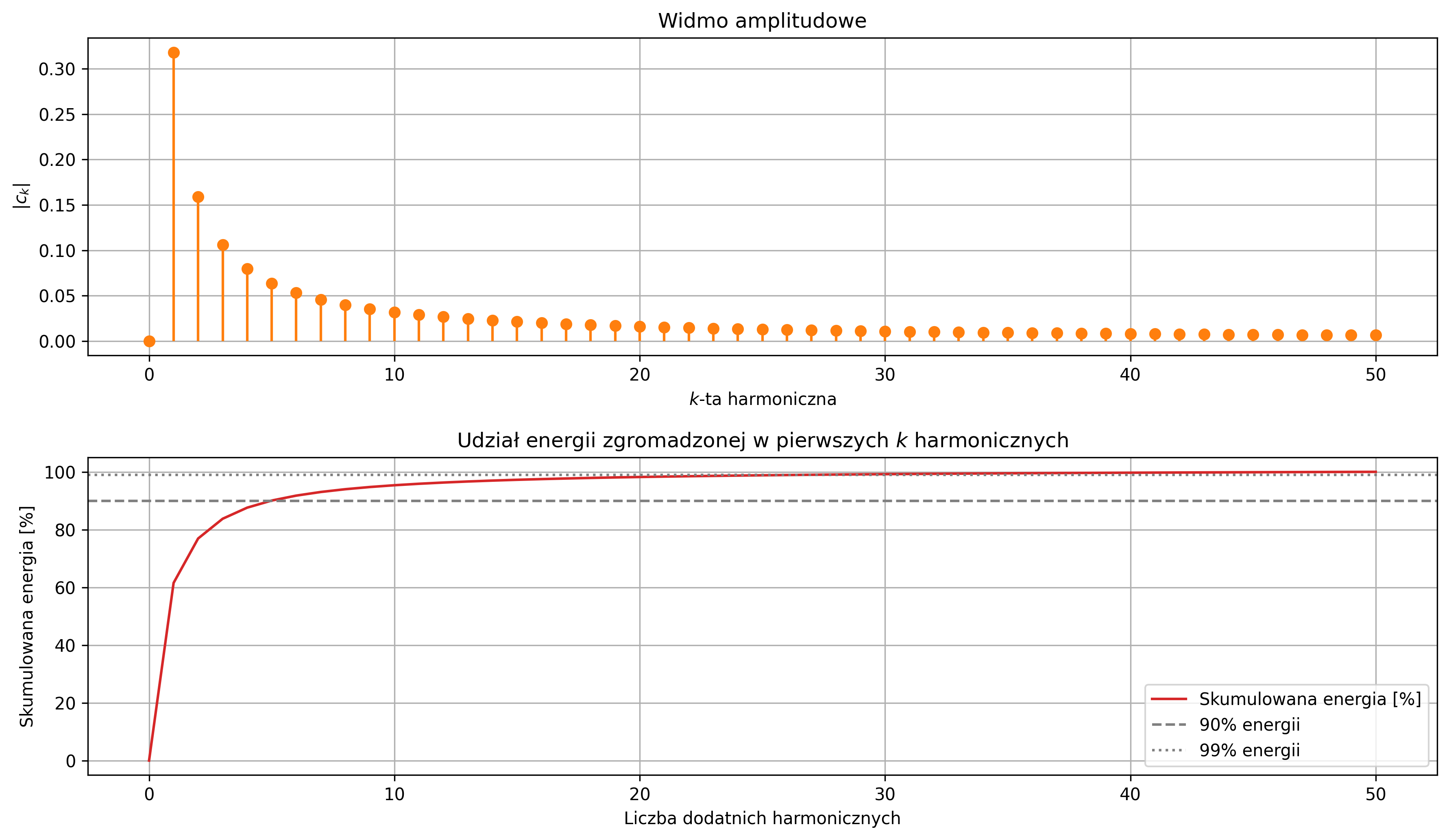
W praktyce można obliczyć, jak szybko kumuluje się energia sygnału w kolejnych harmonicznych – ile energii jest zawartej w kilku pierwszych harmonicznych. Na rys. 4.5 przedstawiono wykres udziału energii zgromadzonej w pierwszych \(k\) harmonicznych. Ponieważ widmo amplitudowe jest symetryczne względem składowej stałej, wykresy są sporządzone tylko dla składowej stałej i dodatnich harmonicznych – stanowi to całkowitą reprezentację widmową. Wykres skumulowanej energii pokazuje, że około \(90\%\) energii uzyskujemy przy około \(25\) harmonicznych, zaś \(99\%\) osiągane jest dla około \(50-54\) harmonicznych.
.png)
