Podręcznik
4. Analiza częstotliwościowa sygnałów
4.7. FFT w języku Python
Zakres ćwiczeń obejmuje generowanie i analizę różnych sygnałów w dziedzinie czasu i częstotliwości. W zadaniach przewidziano m.in.: przybliżanie sygnałów trójkątnych i prostokątnych za pomocą szeregu Fouriera, rysowanie przebiegów w dziedzinie czasu, wyznaczanie widm amplitudowych i fazowych, obliczanie energii sygnałów z użyciem równania Parsevala, stosowanie dyskretnej transformaty Fouriera dla sygnałów złożonych, analizę wpływu parametrów okien czasowych (prostokątne, Hamming, Blackman) na widmo, oraz badanie wpływu liczby punktów DFT na rozdzielczość częstotliwościową sygnałów. Ćwiczenia obejmują sygnały sinusoidalne, piłokształtne, prostokątne i ich kombinacje, z uwzględnieniem różnych częstotliwości próbkowania i długości próbek.
Poniższe przykłady przedstawiają pełne kody źródłowe w języku Python, opracowane na potrzeby realizacji poszczególnych zadań. Do wykonania przedstawionych zadań wymagane jest wykorzystanie następujących bibliotek języka Python:
import numpy as np # obliczenia numeryczne i tablice
import matplotlib.pyplot as plt # tworzenie wykresów ciągłych i dyskretnych
import scipy.signal as signal # generowanie standardowych sygnałów
from numpy.fft import fft, fftfreq # obliczanie dyskretnej transformaty Fouriera
# i wyznaczanie osi częstotliwości
oraz wymagana jest znajomość między innymi następujących poleceń i funkcji języka Python:
fft # obliczanie dyskretnej transformaty Fouriera (algorytm FFT)
fftfreq # wyznaczanie wektora częstotliwości odpowiadającego FFT
fftshift # przesunięcie widma tak, aby zero częstotliwości było w środku
abs # obliczanie modułu widma (amplituda)
trapezoid # obliczanie całki numeryczną metodą trapezów
hamming # okno Hamminga do ograniczenia przecieku widmowego
blackman # okno Blackmana o silnym tłumieniu listków bocznych
Poniżej znajdują się ćwiczenia z przykładową implementacją. Autor zachęca czytelnika do realizacji poniższych kodów oraz do analizy różnych parametrów związanych z wyznaczaniem DFT, poprzez ich modyfikację.
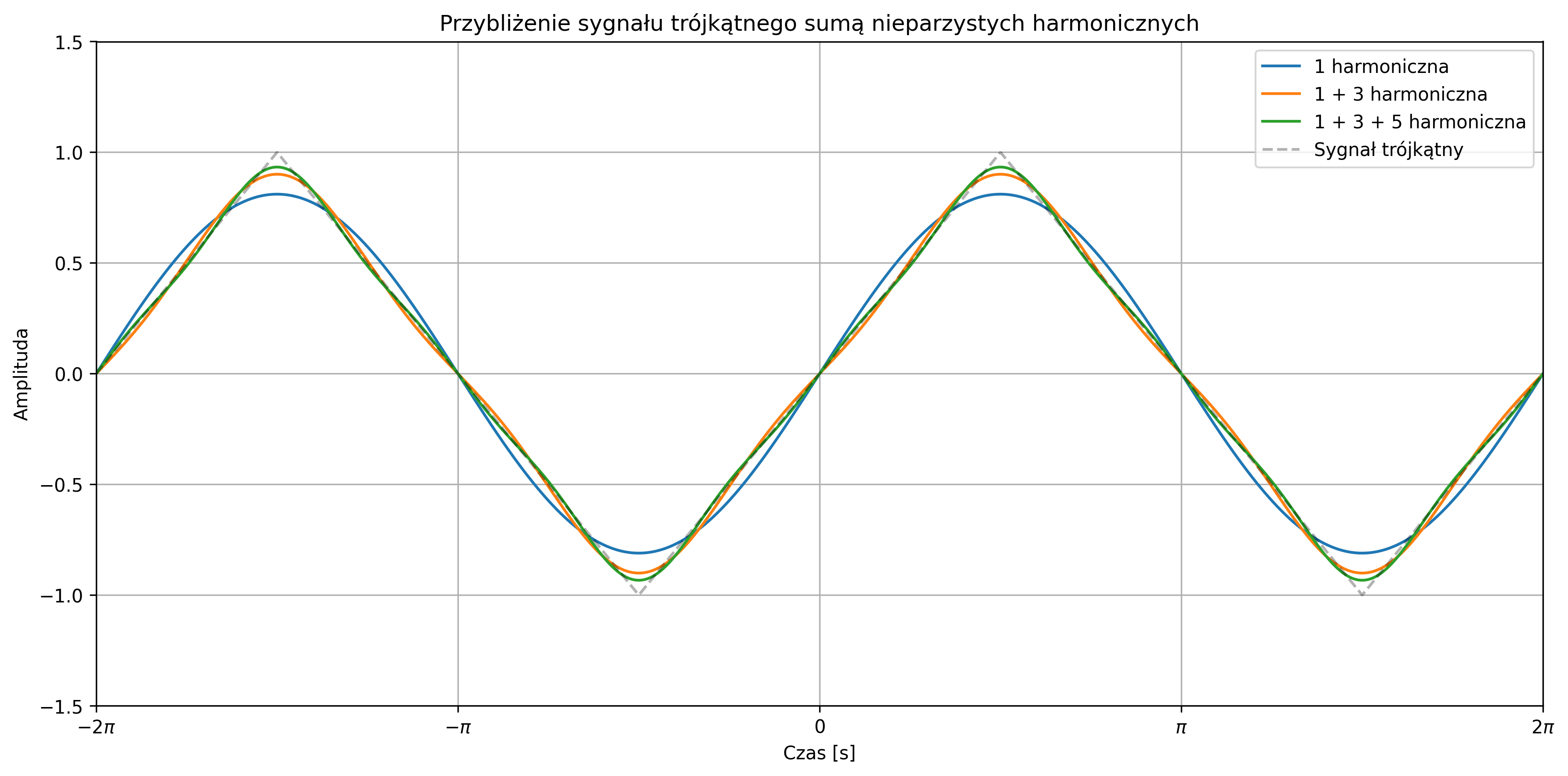
Przybliżyć sygnał trójkątny z wykorzystaniem rozwinięcia w szereg Fouriera o wartościach z przedziału \([-1,1]\) i okresie \( T = 2\pi \):
Wykorzystać \(3\) pierwsze harmoniczne:
import numpy as np
import matplotlib.pyplot as plt
# Czas: 2 okresy
t = np.linspace(-2*np.pi, 2*np.pi, 2000)
# Stała z rozwinięcia Fouriera dla sygnału trójkątnego
A = 8 / (np.pi**2)
# Przybliżenia
f1 = A * ((-1)**0 / (1**2) * np.sin(1*t))
f2 = A * ((-1)**0 / (1**2) * np.sin(1*t) +
(-1)**1 / (3**2) * np.sin(3*t))
f3 = A * ((-1)**0 / (1**2) * np.sin(1*t) +
(-1)**1 / (3**2) * np.sin(3*t) +
(-1)**2 / (5**2) * np.sin(5*t))
# Idealny sygnał trójkątny
triangle_wave = 2/np.pi * np.arcsin(np.sin(t)) # okres 2*pi
# Wykres
plt.figure(figsize=(12, 6))
plt.plot(t, f1, label='1 harmoniczna')
plt.plot(t, f2, label='1 + 3 harmoniczna')
plt.plot(t, f3, label='1 + 3 + 5 harmoniczna')
plt.plot(t, triangle_wave, 'k--', alpha=0.3, label='Sygnał trójkątny')
plt.title('Przybliżenie sygnału trójkątnego sumą nieparzystych harmonicznych')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
plt.legend()
plt.ylim(-1.5, 1.5)
plt.xlim(-2*np.pi, 2*np.pi)
plt.xticks(np.arange(-2*np.pi, 2.5*np.pi, np.pi),
[r'$-2\pi$', r'$-\pi$', '0', r'$\pi$', r'$2\pi$'])
plt.tight_layout()
plt.show()
Narysować przebieg czterech okresów sygnału trójkątnego w dziedzinie czasu. Korzystając z wykładniczej postaci szeregu Fouriera narysować widmo amplitudowe \(|c_k|\) i fazowe \(\varphi_k\).
Amplitudy są zgodne z rozwinięciem Fouriera dla sygnału trójkątnego:co można również zapisać w formie:
dla nieparzystego numeru harmonicznej \( k=1,3,5,\ldots \).
Ponieważ jest to sygnał nieparzysty (w wersji sinusowej), fazy są tylko \(0\) lub \(\pi\).
import numpy as np
import matplotlib.pyplot as plt
# Parametry
T = 2 * np.pi # okres sygnału
t = np.linspace(-2*T, 2*T, 1000) # 4 okresy
# Idealny sygnał trójkątny (okres 2*pi, amplituda [-1, 1])
triangle_wave = 2/np.pi * np.arcsin(np.sin(t))
# Liczba harmonicznych
N = 25
k = np.arange(1, 2*N, 2) # nieparzyste harmoniczne: 1, 3, 5, ...
# Współczynnik znaku (-1)^k, gdzie k := (k-1)/2
signs = (-1)**((k - 1) // 2)
# Amplitudy z uwzględnieniem spadku 1/n^2 i znaku
ak = (8 / (np.pi**2)) * signs / (k**2)
# Widmo amplitudowe (moduł ak)
amplitudes = np.abs(ak)
# Widmo fazowe: 0 dla dodatnich współczynników, pi dla ujemnych
phases = np.where(signs > 0, 0, np.pi)
# Wykresy
plt.figure(figsize=(10, 8))
# 1. Sygnał trójkątny
plt.subplot(3, 1, 1)
plt.plot(t, triangle_wave, color='C0')
plt.title('Sygnał trójkątny w dziedzinie czasu')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
# 2. Widmo amplitudowe
plt.subplot(3, 1, 2)
plt.stem(k, amplitudes, linefmt='C1-', markerfmt='C1o', basefmt=" ")
plt.title('Widmo amplitudowe')
plt.xlabel(rf'$k$-ta harmoniczna')
plt.ylabel(rf'Amplituda $A_k$')
plt.grid(True)
# 3. Widmo fazowe
plt.subplot(3, 1, 3)
plt.stem(k, phases, linefmt='C2-', markerfmt='C2o', basefmt=" ")
plt.title('Widmo fazowe')
plt.xlabel(rf'$k$-ta harmoniczna')
plt.ylabel(rf'Faza $\varphi_k$ [rad]')
plt.yticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
[r"$-\pi$", r"$-\pi/2$", "0", r"$\pi/2$", r"$\pi$"])
plt.grid(True)
plt.tight_layout()
plt.show()
.png)
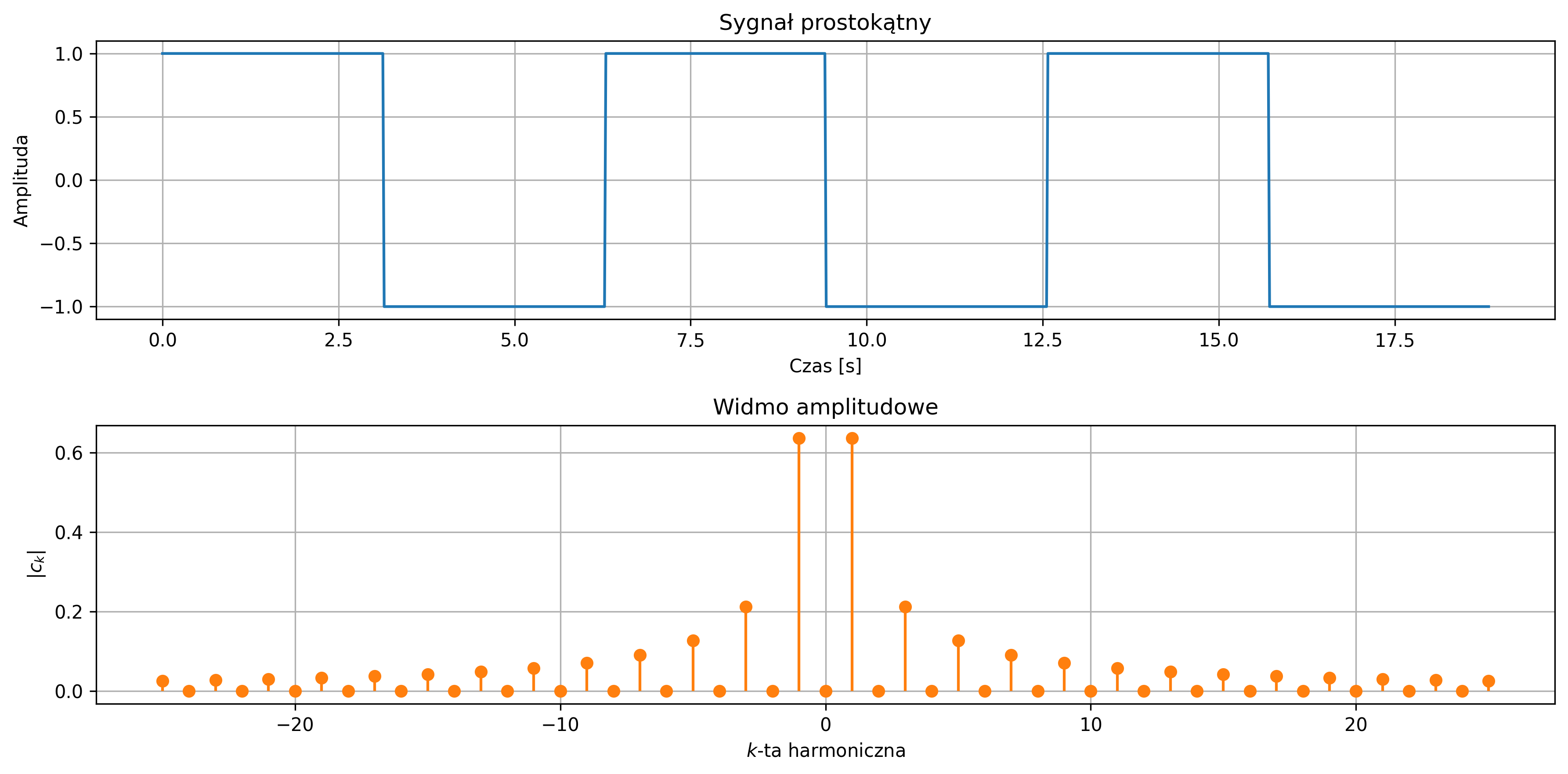
Narysować przebieg trzech okresów sygnału prostokątnego oraz jego widmo amplitudowe \(|c_k|\). Korzystając z równania Parsevala:
obliczyć energię sygnału (w jednym okresie podzieloną przez długość okresu) jako sumę kwadratów modułów współczynników Fouriera, czyli „mocy” poszczególnych harmonicznych.
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import square
# Parametry sygnału
T = 2 * np.pi # okres sygnału
f = 1 / T # częstotliwość podstawowa
num_periods = 3 # liczba okresów do rysowania
t = np.linspace(0, num_periods * T, 3000, endpoint=False)
# Sygnał prostokątny
x = square(2 * np.pi * f * t, duty=0.5)
# Zespolony szereg Fouriera
N = 25 # liczba harmonicznych
k = np.arange(-N, N + 1) # indeksy harmonicznych
# Współczynniki zespolone szeregu Fouriera dla sygnału prostokątnego
def c_k_fun(ki):
if ki == 0:
return 0
elif ki % 2 == 0:
return 0
else:
return 2 / (1j * ki * np.pi)
# Wektor współczynników
c_k = np.array([c_k_fun(ki) for ki in k])
# Sprawdzenie tożsamości Parsevala (1 okres)
t_single = np.linspace(0, T, 4000, endpoint=False)
x_single = square(2 * np.pi * f * t_single, duty=0.5)
energy_time = (1 / T) * np.trapezoid(np.abs(x_single)**2, t_single)
energy_freq = np.sum(np.abs(c_k)**2)
print(f'Energia w dziedzinie czasu: {energy_time:.6f}')
print(f'Suma |c_k|^2: {energy_freq:.6f}')
# Wykresy
plt.figure(figsize=(12, 7))
# Sygnał w dziedzinie czasu
plt.subplot(2, 1, 1)
plt.plot(t, x, color='C0')
plt.title('Sygnał prostokątny')
plt.xlabel('Czas [s]')
plt.ylabel('Amplituda')
plt.grid(True)
# Widmo amplitudowe współczynników c_k
plt.subplot(2, 1, 2)
plt.stem(k, np.abs(c_k), linefmt='C1-', markerfmt='C1o', basefmt=" ")
plt.title('Widmo amplitudowe zespolonego szeregu Fouriera')
plt.xlabel(rf'$k$-ta harmoniczna')
plt.ylabel(rf'$|c_k|$')
plt.grid(True)
plt.tight_layout()
plt.show()
Korzystając z algorytmu FFT narysować widmo amplitudowe i fazowe DFT dla sygnału, będącego sumą dwóch kosinusów i dwóch sinusów:
Przyjąć, że \( f_s = N = 32 \), żeby łatwo przekształcać indeksy prążków na ich częstotliwości:
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft
# Parametry sygnału
N = 32
n = np.arange(N)
# Mieszana suma: kosinus + sinus
x = (np.cos(2 * np.pi * 3 * n / N) # kosinus 3
- np.cos(2 * np.pi * 5 * n / N) # kosinus 5 z ujemną amplitudą
+ np.sin(2 * np.pi * 7 * n / N) # sinus 7
- 0.5 * np.sin(2 * np.pi * 9 * n / N)) # sinus 9 z ujemną amplitudą
# Znormalizowana DFT
X = fft(x) / N
k = np.arange(N)
# Moduł i faza
amplitude = np.abs(X)
phase = np.angle(X)
# Wykresy
plt.figure(figsize=(12, 6))
# Widmo amplitudowe
plt.subplot(2, 1, 1)
plt.stem(k, amplitude, linefmt='C1-', markerfmt='C1o', basefmt='k-')
plt.title('Widmo amplitudowe')
plt.xlabel(r'$k$')
plt.ylabel(r'$|X[k]|$')
# Oznaczenie harmonicznych
harmonics = [3, 5, 7, 9, N - 3, N - 5, N - 7, N - 9]
for h in harmonics:
plt.annotate(f'harm. {h}',
xy=(h, amplitude[h]),
xytext=(h, amplitude[h] + 0.05),
arrowprops=dict(facecolor='black', arrowstyle='->'),
ha='center')
# Widmo fazowe
plt.subplot(2, 1, 2)
plt.stem(k, phase, linefmt='C2-', markerfmt='C2o', basefmt='k-')
plt.title('Widmo fazowe')
plt.xlabel(r'$k$')
plt.ylabel(r'$\arg\,X[k]$')
# Oś Y w jednostkach pi
ticks = np.pi * np.array([-1, -0.5, 0, 0.5, 1])
labels = [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$\pi/2$', r'$\pi$']
plt.yticks(ticks, labels)
plt.tight_layout()
plt.show()
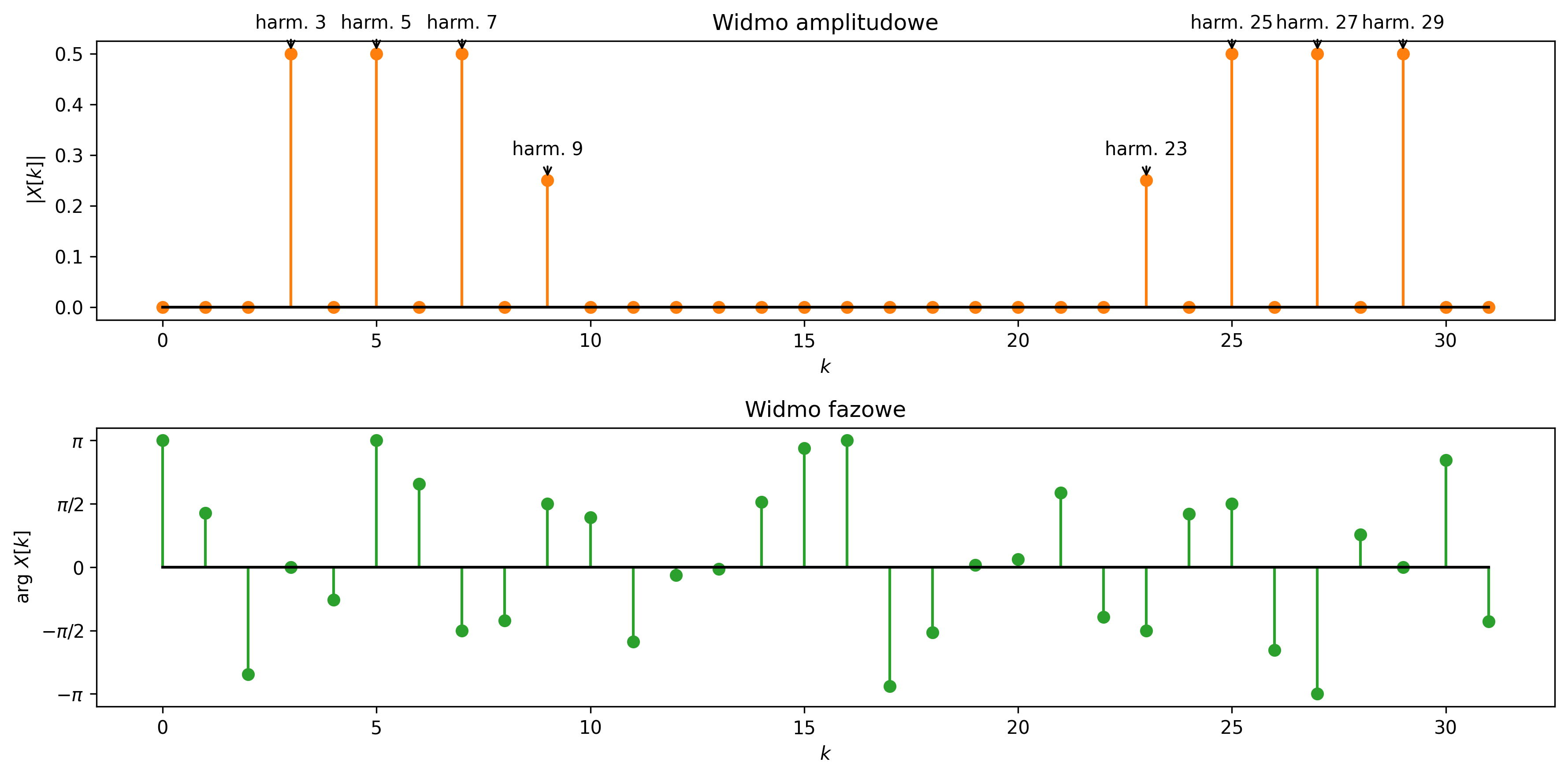
Każdy z symetrycznych prążków (bo sygnał rzeczywisty) zawiera połowę amplitudy składowej sygnału. Zatem suma amplitud prążków symetrycznych daje rzeczywistą amplitudę składowych sinusoidalnych. Każdy prążek widma wskazuje na obecność składowej o częstotliwości i amplitudzie:
- prążki w \( k=3 \) i \( k=29 \) wskazują obecność składowych o \(3\) i \(29\) jednostkach częstotliwości, które mają wysokość \(\approx 0.5\),
- prążki w \( k=5 \) i \( k=27 \) wskazują obecność składowych o \(5\) i \(27\) jednostkach częstotliwości, które mają wysokość \(\approx 0.5\),
- prążki w \( k=7 \) i \( k=25 \) wskazują obecność składowych o \(7\) i \(25\) jednostkach częstotliwości, które mają wysokość \(\approx 0.5\),
- prążki w \( k=9 \) i \( k=23 \) wskazują obecność składowych o \(9\) i \(23\) jednostkach częstotliwości, które mają wysokość \(\approx 0.25\).
Zauważmy, że ujemne wartości amplitudy zmieniają się tylko w niezerowe przesunięcia fazowe, np.:
Z wykresu fazowego możemy odczytać, że dla kosinusów faza wynosi \(0\) lub \(\pi\), a dla sinusów faza wynosi \(\pm\frac{\pi}{2}\) w zależności od znaku amplitudy.
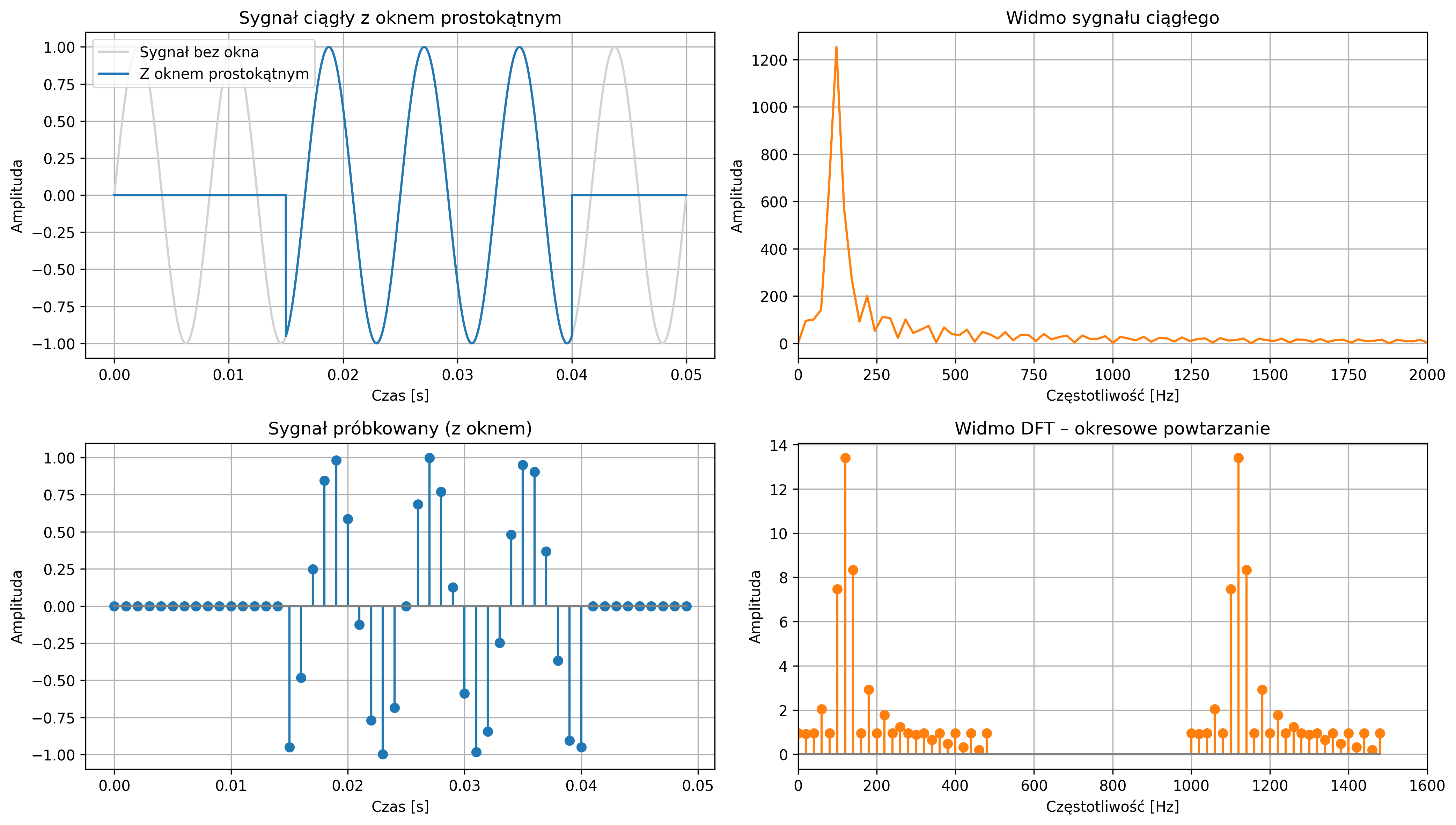
Rozważmy sygnał sinusoidalny o częstotliwości \(120\) Hz. Wyznaczyć widmo amplitudowe sygnału ciągłego trwającego \(0.05\) s z nałożonym oknem prostokątnym o szerokości od \(0.015\) s do \(0.04\) s oraz widmo sygnału dyskretnego, dla częstotliwości próbkowania \(1000\) Hz.
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq, fftshift
# Parametry sygnału
f = 120 # Hz
fs = 1000 # częstotliwość próbkowania
T = 1 / fs # okres próbkowania
t_max = 0.05 # krótki odcinek czasu trwania sygnału
t_cont = np.linspace(0, t_max, 5000) # chcemy trakotować jako ciągły
x_cont = np.sin(2 * np.pi * f * t_cont)
# Okno prostokątne (na sygnale ciągłym)
window = np.where((t_cont >= 0.015) & (t_cont <= 0.04), 1, 0)
x_cont_win = x_cont * window
# FFT sygnału ciągłego
N_fft = 4096 # rozmiar transformaty
X_fft = fft(x_cont_win, N_fft)
freqs_fft = fftfreq(N_fft, d=t_cont[1] - t_cont[0]) # krok czasowy ok. 1e-5
# odpowiada to próbkowaniu z dużym fs ok. 100 KHz
X_fft_shifted = fftshift(X_fft) # przesunięcie - częstotliwości od 0
freqs_fft_shifted = fftshift(freqs_fft)
X_fft_pos = np.abs(X_fft_shifted[N_fft//2:])
freqs_fft_pos = freqs_fft_shifted[N_fft//2:]
# Próbkowanie
t_disc = np.arange(0, t_max, T)
x_disc = np.sin(2 * np.pi * f * t_disc)
window_disc = np.where((t_disc >= 0.015) & (t_disc <= 0.04), 1, 0)
x_disc_win = x_disc * window_disc
# DFT
N = len(x_disc_win)
X_dft = fft(x_disc_win)
freqs_dft = fftfreq(N, d=T)
X_dft_pos = np.abs(X_dft[:N // 2])
freqs_dft_pos = freqs_dft[:N // 2]
# Powielone widmo DFT – okresowość
repeats = 2 # 2 okresy
rep_freqs = np.concatenate([freqs_dft_pos + i * fs for i in range(repeats)])
rep_mags = np.tile(X_dft_pos, repeats)
rep_indices = np.concatenate([np.arange(N // 2) + i * (N // 2) for i in range(repeats)])
rep_mags = np.tile(X_dft_pos, repeats)
# Wykresy
fig, axs = plt.subplots(2, 2, figsize=(14, 8))
# Sygnał ciągły + okno
axs[0, 0].plot(t_cont, x_cont, color='lightgray', label='Sygnał bez okna')
axs[0, 0].plot(t_cont, x_cont_win, color='C0', label='Z oknem prostokątnym')
axs[0, 0].set_title('Sygnał ciągły z oknem prostokątnym')
axs[0, 0].set_xlabel('Czas [s]')
axs[0, 0].set_ylabel('Amplituda')
axs[0, 0].legend()
axs[0, 0].grid()
# Widmo sygnału ciągłego
axs[0, 1].plot(freqs_fft_pos, X_fft_pos, color='C1')
axs[0, 1].set_xlim(0, 2000) # widmo sięga fs/2, czyli ok. 50 kHz
# ograniczamy do 2000 w celu lepszej wizualizacji
axs[0, 1].set_title('Widmo sygnału ciągłego')
axs[0, 1].set_xlabel('Częstotliwość [Hz]')
axs[0, 1].set_ylabel('Amplituda')
axs[0, 1].grid()
# Sygnał próbkowany
axs[1, 0].stem(t_disc, x_disc_win, linefmt='C0-', markerfmt='C0o', basefmt='gray')
axs[1, 0].set_title('Sygnał próbkowany (z oknem)')
axs[1, 0].set_xlabel('Czas [s]')
axs[1, 0].set_ylabel('Amplituda')
axs[1, 0].grid()
# Widmo DFT (powtarzalność)
axs[1, 1].stem(rep_freqs, rep_mags, linefmt='C1-', markerfmt='C1o', basefmt='gray')
axs[1, 1].set_xlim(0, 1600) # aby pokazać 2 okresy
axs[1, 1].set_title('Widmo DFT – okresowe powtarzanie')
axs[1, 1].set_xlabel('Częstotliwość [Hz]')
axs[1, 1].set_ylabel('Amplituda')
axs[1, 1].grid()
plt.tight_layout()
plt.show()
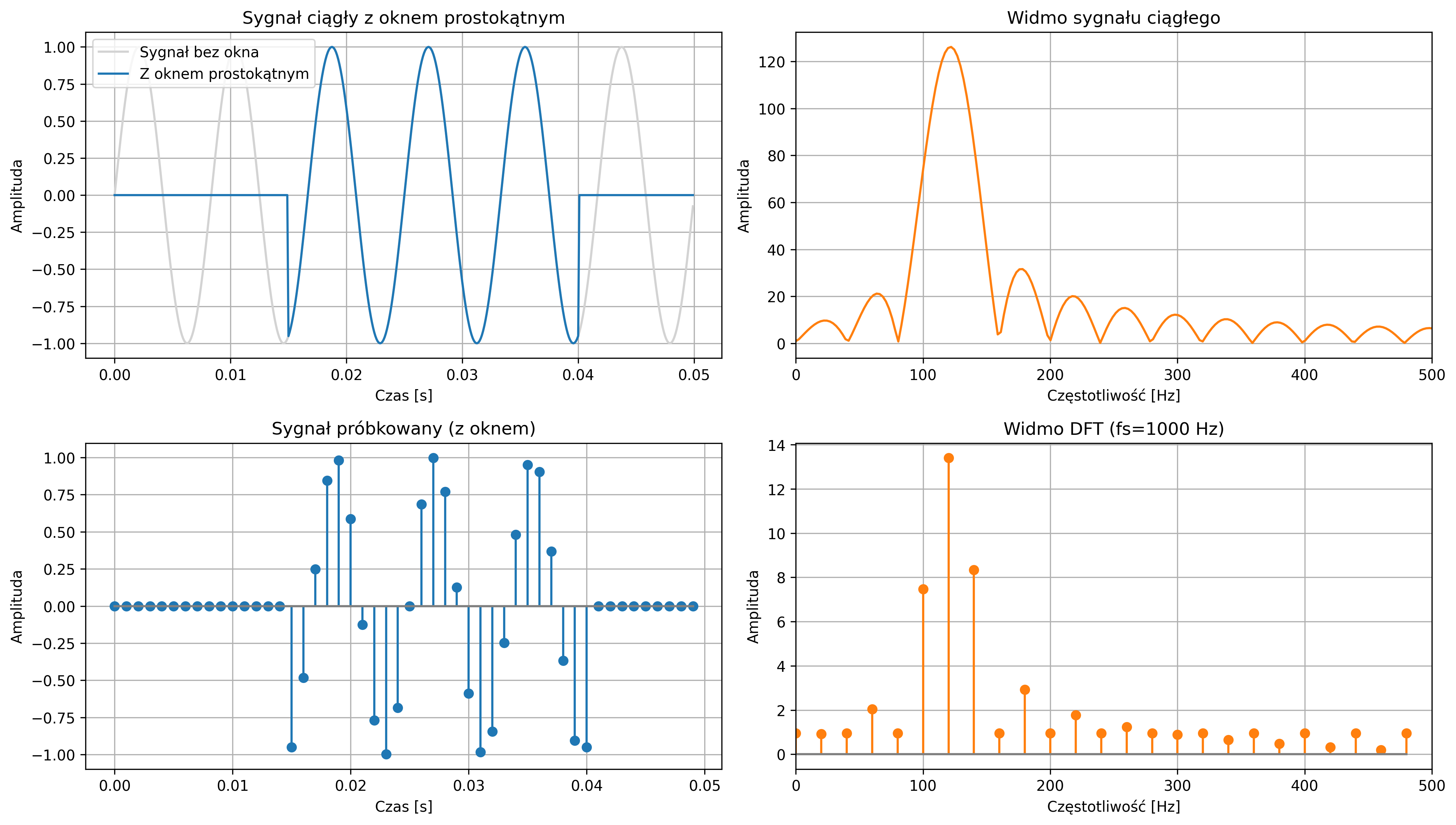
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
# Parametry sygnału
f = 120 # Hz
fs = 1000 # częstotliwość próbkowania
T = 1 / fs # okres próbkowania
t_max = 0.05 # krótki odcinek czasu trwania sygnału
# sygnał ciągły (symulowany gęstą siatką, np. 10x gęściej)
oversampling = 10
t_cont = np.linspace(0, t_max, int(fs * oversampling * t_max), endpoint=False)
x_cont = np.sin(2 * np.pi * f * t_cont)
# Okno prostokątne (na sygnale ciągłym)
window = np.where((t_cont >= 0.015) & (t_cont <= 0.04), 1, 0)
x_cont_win = x_cont * window
# FFT sygnału ciągłego
N_fft = 4096 # rozmiar transformaty
X_fft = fft(x_cont_win, N_fft)
freqs_fft = fftfreq(N_fft, d=1/(fs*oversampling))
X_fft_pos = np.abs(X_fft[:N_fft//2])
freqs_fft_pos = freqs_fft[:N_fft//2]
# Sygnał próbkowany zgodnie z fs
t_disc = np.arange(0, t_max, T)
x_disc = np.sin(2 * np.pi * f * t_disc)
window_disc = np.where((t_disc >= 0.015) & (t_disc <= 0.04), 1, 0)
x_disc_win = x_disc * window_disc
# DFT
N = len(x_disc_win)
X_dft = fft(x_disc_win)
freqs_dft = fftfreq(N, d=T)
X_dft_pos = np.abs(X_dft[:N // 2])
freqs_dft_pos = freqs_dft[:N // 2]
# Wykresy
fig, axs = plt.subplots(2, 2, figsize=(14, 8))
# Sygnał ciągły + okno
axs[0, 0].plot(t_cont, x_cont, color='lightgray', label='Sygnał bez okna')
axs[0, 0].plot(t_cont, x_cont_win, color='C0', label='Z oknem prostokątnym')
axs[0, 0].set_title('Sygnał ciągły z oknem prostokątnym')
axs[0, 0].set_xlabel('Czas [s]')
axs[0, 0].set_ylabel('Amplituda')
axs[0, 0].legend()
axs[0, 0].grid()
# Widmo sygnału ciągłego
axs[0, 1].plot(freqs_fft_pos, X_fft_pos, color='C1')
axs[0, 1].set_xlim(0, fs/2) # pasmo Nyquista
axs[0, 1].set_title('Widmo sygnału ciągłego')
axs[0, 1].set_xlabel('Częstotliwość [Hz]')
axs[0, 1].set_ylabel('Amplituda')
axs[0, 1].grid()
# Sygnał próbkowany
axs[1, 0].stem(t_disc, x_disc_win, linefmt='C0-', markerfmt='C0o', basefmt='gray')
axs[1, 0].set_title('Sygnał próbkowany (z oknem)')
axs[1, 0].set_xlabel('Czas [s]')
axs[1, 0].set_ylabel('Amplituda')
axs[1, 0].grid()
# Widmo DFT
axs[1, 1].stem(freqs_dft_pos, X_dft_pos, linefmt='C1-', markerfmt='C1o', basefmt='gray')
axs[1, 1].set_xlim(0, fs/2)
axs[1, 1].set_title('Widmo DFT (fs=1000 Hz)')
axs[1, 1].set_xlabel('Częstotliwość [Hz]')
axs[1, 1].set_ylabel('Amplituda')
axs[1, 1].grid()
plt.tight_layout()
plt.show()
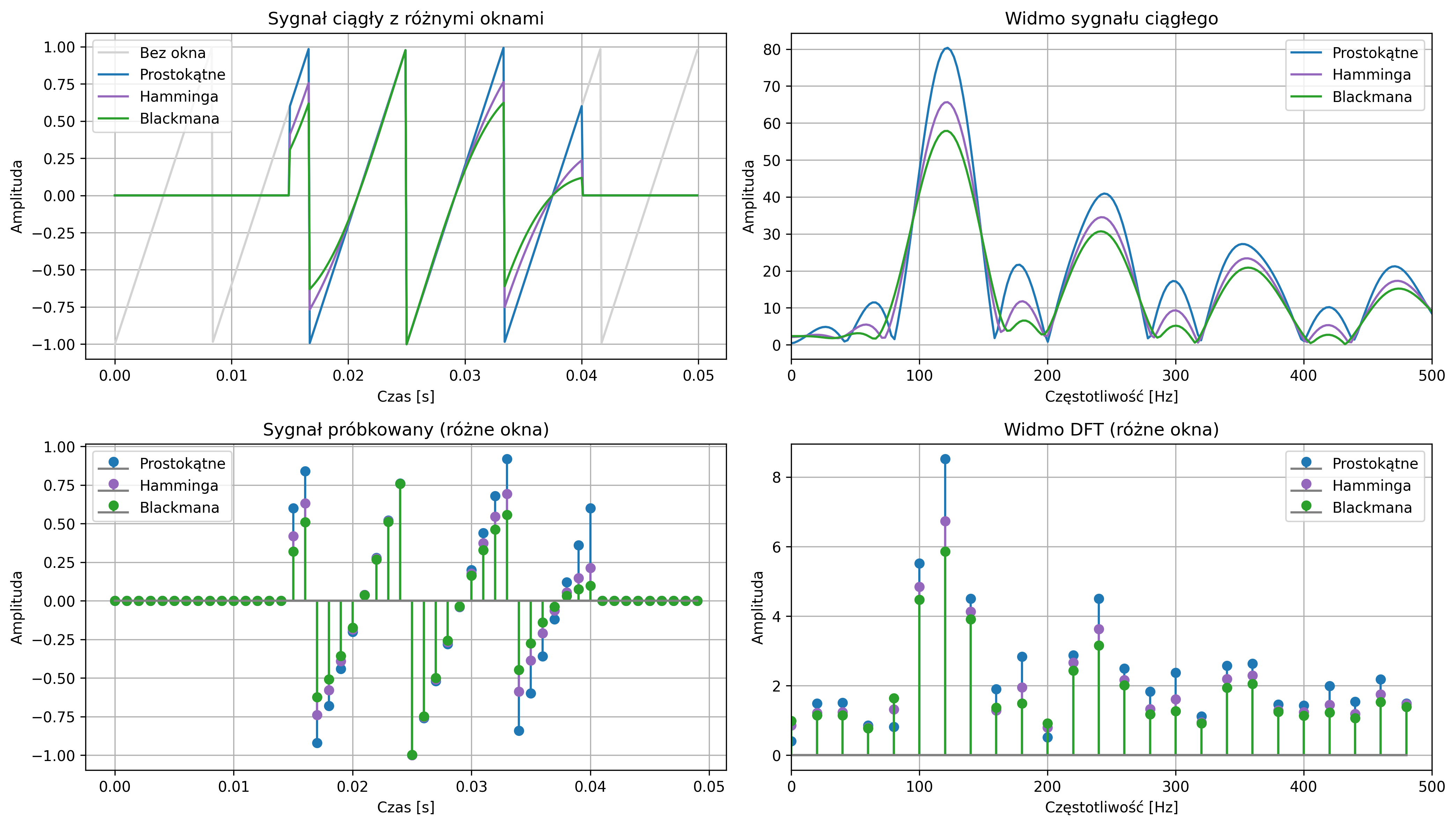
Rozważmy sygnał piłokształtny o częstotliwości \(120\) Hz. Wyznaczyć widmo amplitudowe sygnału ciągłego trwającego \(0.05\) s z nałożonym oknem prostokątnym o szerokości od \(0.015\) s do \(0.04\) s oraz widmo sygnału dyskretnego, dla częstotliwości próbkowania \(1000\) Hz. Zilustrować wpływ użytej funkcji na kształt otrzymanego widma - wykorzystać okno Hamminga i Blackmanna.
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
from scipy.signal import sawtooth, windows
# Parametry sygnału
f = 120 # Hz
fs = 1000 # częstotliwość próbkowania
T = 1 / fs # okres próbkowania
t_max = 0.05 # czas trwania sygnału
# sygnał ciągły (symulowany gęstą siatką, np. 10x gęściej)
oversampling = 10
t_cont = np.linspace(0, t_max, int(fs * oversampling * t_max), endpoint=False)
x_cont = sawtooth(2 * np.pi * f * t_cont) # sygnał piłokształtny
# Okna (na sygnale ciągłym)
N_cont = len(t_cont)
win_rect = np.where((t_cont >= 0.015) & (t_cont <= 0.04), 1, 0) # prostokątne
win_hamm = windows.hamming(N_cont) * win_rect # Hamming
win_black = windows.blackman(N_cont) * win_rect # Blackmann
# Nałożone sygnały
x_cont_rect = x_cont * win_rect
x_cont_hamm = x_cont * win_hamm
x_cont_black = x_cont * win_black
# FFT sygnału ciągłego z różnymi oknami
N_fft = 4096
freqs_fft = fftfreq(N_fft, d=1/(fs*oversampling))
def fft_mag(x):
X = fft(x, N_fft)
return np.abs(X[:N_fft//2])
freqs_fft_pos = freqs_fft[:N_fft//2]
X_fft_rect = fft_mag(x_cont_rect)
X_fft_hamm = fft_mag(x_cont_hamm)
X_fft_black = fft_mag(x_cont_black)
# Sygnał próbkowany (dla porównania)
t_disc = np.arange(0, t_max, T)
x_disc = sawtooth(2 * np.pi * f * t_disc)
N_disc = len(t_disc)
# Te same okna dyskretne
win_rect_d = np.where((t_disc >= 0.015) & (t_disc <= 0.04), 1, 0)
win_hamm_d = windows.hamming(N_disc) * win_rect_d
win_black_d = windows.blackman(N_disc) * win_rect_d
x_disc_rect = x_disc * win_rect_d
x_disc_hamm = x_disc * win_hamm_d
x_disc_black = x_disc * win_black_d
# FFT dla sygnałów dyskretnych
def dft_mag(x):
X = fft(x)
return np.abs(X[:len(x)//2]), fftfreq(len(x), d=T)[:len(x)//2]
X_dft_rect, freqs_dft_pos = dft_mag(x_disc_rect)
X_dft_hamm, _ = dft_mag(x_disc_hamm)
X_dft_black, _ = dft_mag(x_disc_black)
# Wykresy
fig, axs = plt.subplots(2, 2, figsize=(14, 8))
# Sygnał ciągły z oknami
axs[0, 0].plot(t_cont, x_cont, color='lightgray', label='Bez okna')
axs[0, 0].plot(t_cont, x_cont_rect, label='Prostokątne', color='C0')
axs[0, 0].plot(t_cont, x_cont_hamm, label='Hamminga', color='C4')
axs[0, 0].plot(t_cont, x_cont_black, label='Blackmana', color='C2')
axs[0, 0].set_title('Sygnał ciągły z różnymi oknami')
axs[0, 0].set_xlabel('Czas [s]')
axs[0, 0].set_ylabel('Amplituda')
axs[0, 0].legend()
axs[0, 0].grid()
# Widma ciągłe
axs[0, 1].plot(freqs_fft_pos, X_fft_rect, label='Prostokątne', color='C0')
axs[0, 1].plot(freqs_fft_pos, X_fft_hamm, label='Hamminga', color='C4')
axs[0, 1].plot(freqs_fft_pos, X_fft_black, label='Blackmana', color='C2')
axs[0, 1].set_xlim(0, fs/2)
axs[0, 1].set_title('Widmo sygnału ciągłego')
axs[0, 1].set_xlabel('Częstotliwość [Hz]')
axs[0, 1].set_ylabel('Amplituda')
axs[0, 1].legend()
axs[0, 1].grid()
# Sygnały dyskretne
axs[1, 0].stem(t_disc, x_disc_rect, linefmt='C0-', markerfmt='C0o', basefmt='gray', label='Prostokątne')
axs[1, 0].stem(t_disc, x_disc_hamm, linefmt='C4-', markerfmt='C4o', basefmt='gray', label='Hamminga')
axs[1, 0].stem(t_disc, x_disc_black, linefmt='C2-', markerfmt='C2o', basefmt='gray', label='Blackmana')
axs[1, 0].set_title('Sygnał próbkowany (różne okna)')
axs[1, 0].set_xlabel('Czas [s]')
axs[1, 0].set_ylabel('Amplituda')
axs[1, 0].legend()
axs[1, 0].grid()
# Widma DFT
axs[1, 1].stem(freqs_dft_pos, X_dft_rect, linefmt='C0-', markerfmt='C0o', basefmt='gray', label='Prostokątne')
axs[1, 1].stem(freqs_dft_pos, X_dft_hamm, linefmt='C4-', markerfmt='C4o', basefmt='gray', label='Hamminga')
axs[1, 1].stem(freqs_dft_pos, X_dft_black, linefmt='C2-', markerfmt='C2o', basefmt='gray', label='Blackmana')
axs[1, 1].set_xlim(0, fs/2)
axs[1, 1].set_title('Widmo DFT (różne okna)')
axs[1, 1].set_xlabel('Częstotliwość [Hz]')
axs[1, 1].set_ylabel('Amplituda')
axs[1, 1].legend()
axs[1, 1].grid()
plt.tight_layout()
plt.show()
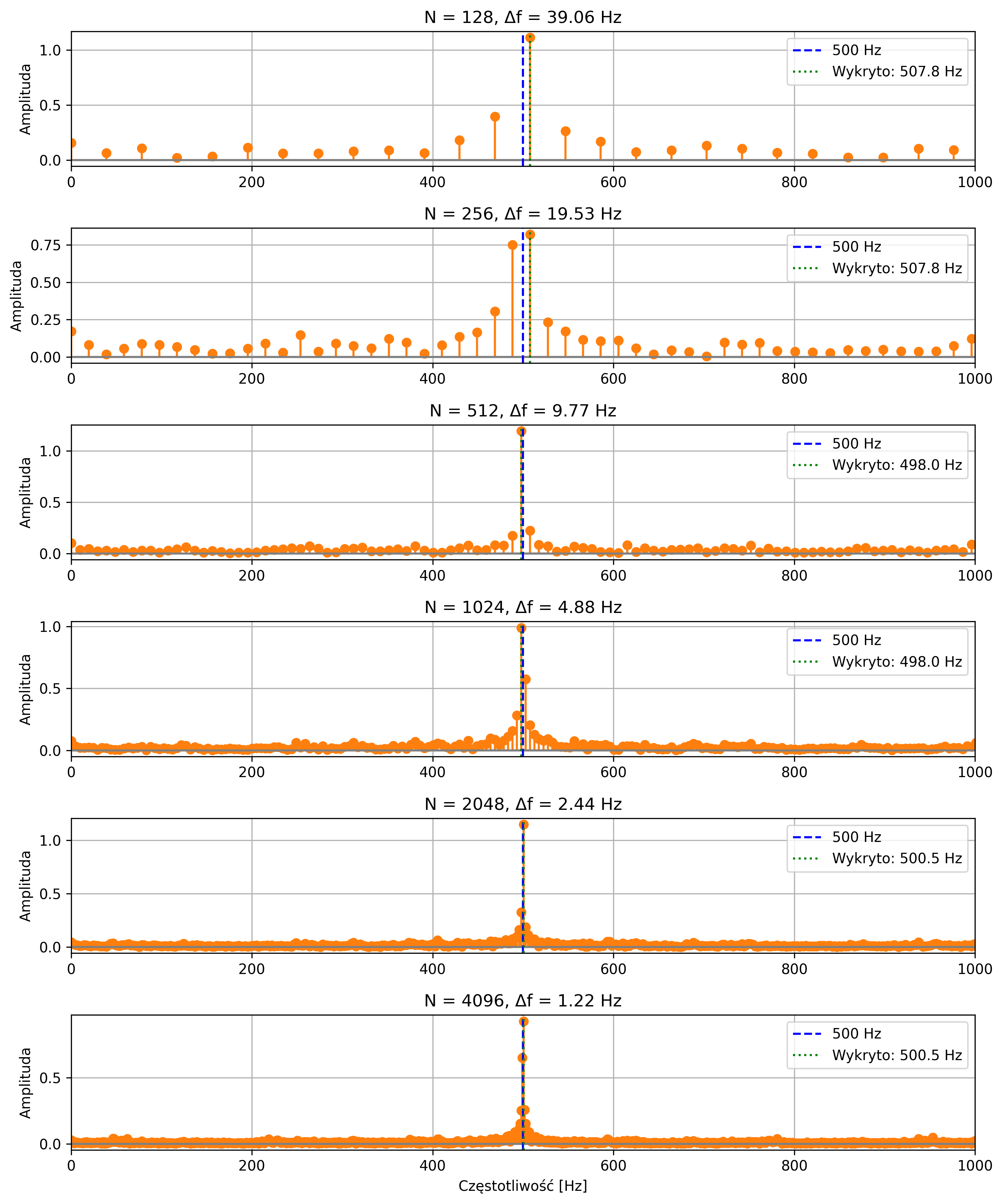
Rozważmy sygnał prostokątny o amplitudzie \(\pm 1\) o częstotliwości \(500\) Hz. Wyznaczyć widmo amplitudowe DFT dla częstotliwości próbkowania \(5000\) Hz. Dokonać analizy wpływu rozmiaru DFT na rozdzielczość częstotliwościową. Przyjąć \( N=128, 256, 1024, 2048, 4096 \).
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
from scipy.signal import square
# Parametry
fs = 5000 # częstotliwość próbkowania
f = 500 # Hz
N_list = [128, 256, 512, 1024, 2048, 4096]
# Wykresy
fig, axs = plt.subplots(len(N_list), 1, figsize=(10, 12), sharex=False)
for i, N in enumerate(N_list):
t = np.arange(N) / fs
# Sygnał prostokątny
x = square(2 * np.pi * f * t)
# FFT
X = fft(x)
freqs = fftfreq(N, d=1/fs)
mag = 2 * np.abs(X[:N // 2]) / N
freqs_pos = freqs[:N // 2]
# Szukanie największego prążka
peak_idx = np.argmax(mag)
peak_freq = freqs_pos[peak_idx]
# Widma DFT
axs[i].stem(freqs_pos, mag, basefmt="gray", linefmt="C1-", markerfmt="C1o")
axs[i].axvline(f, color='blue', linestyle='--', label='500 Hz')
axs[i].axvline(peak_freq, color='green', linestyle=':', label=f'Wykryto: {peak_freq:.1f} Hz')
axs[i].set_title(f'N = {N}, Δf = {fs/N:.2f} Hz')
axs[i].set_xlim(0, 1000)
axs[i].set_ylabel('Amplituda')
axs[i].grid(True)
axs[i].legend()
axs[-1].set_xlabel('Częstotliwość [Hz]')
plt.tight_layout()
plt.show()
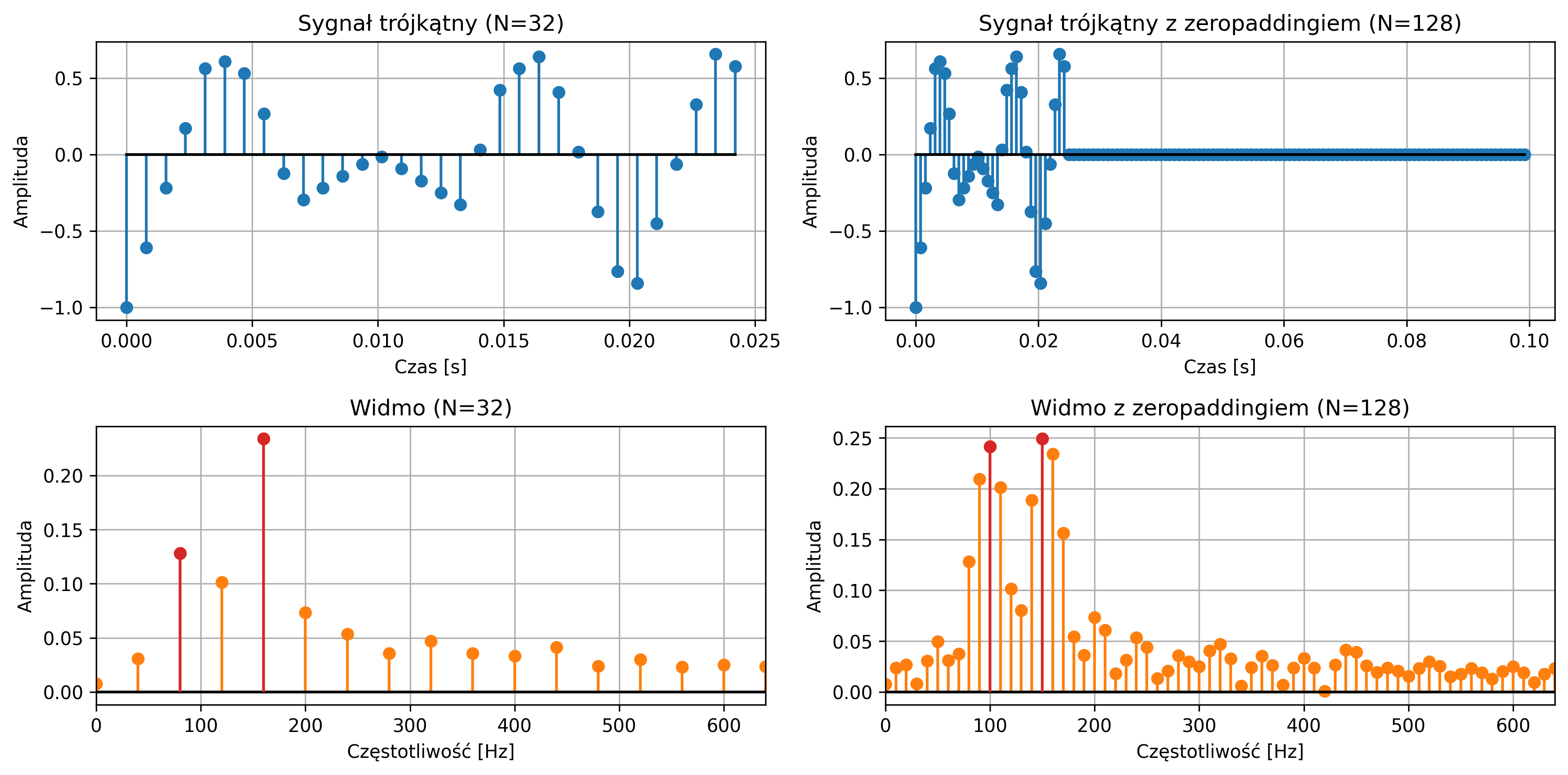
Rozważmy sygnał trójkątny, będący sumą dwóch sygnałów piłokształtnych o współczynniku wypełnienia \(0.5\), amplitudach \(0.5\) i częstotliwościach \(150\) Hz i \(100\) Hz. Przyjmując częstotliwość próbkowania \(1280\) Hz, porównać przebieg \(32\) próbek oryginalnego sygnału i sygnału z dopisanymi 96 zerami na końcu oraz ich widm amplitudowych.
Zauważmy, że rozważać będziemy rozmiary DFT na poziomie: \( N=32 \) oraz \( N=128 \) (po zero-paddingu).
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import sawtooth
from scipy.fft import fft
# Parametry
fs = 1280 # Hz
f1 = 150 # Hz
f2 = 100 # Hz
def signal_triangle(N):
t = np.arange(N) / fs
# Sygnał trójkątny sumą dwóch piłokształtnych o wypełnieniu 0.5
return t, 0.5*sawtooth(2*np.pi*f1*t, 0.5) + 0.5*sawtooth(2*np.pi*f2*t, 0.5)
def spectrum(x, N):
X = fft(x, N) / len(x)
f = np.arange(N) * fs / N
return f, np.abs(X)
# Dwa przypadki
N1 = 32 # oryginalny
t1, x1 = signal_triangle(N1)
f1_spec, X1 = spectrum(x1, N1)
N2 = 128 # zeropadding
t2, x2 = signal_triangle(N1)
f2_spec, X2 = spectrum(x2, N2)
# Harmoniczne do podświetlenia
harmonics = [f1, f2]
# Wykres
fig, axs = plt.subplots(2, 2, figsize=(12, 6))
# Sygnał oryginalny N=32
axs[0, 0].stem(t1, x1, basefmt="k-", linefmt='C0-', markerfmt='C0o')
axs[0, 0].set_title(rf'Sygnał trójkątny ($N$={N1})')
axs[0, 0].set_xlabel('Czas [s]')
axs[0, 0].set_ylabel('Amplituda')
axs[0, 0].grid(True)
# Sygnał z zeropaddingiem N=128
axs[0, 1].stem(np.arange(N2)/fs, np.pad(x2, (0, N2-N1)),
basefmt="k-", linefmt='C0-', markerfmt='C0o')
axs[0, 1].set_title(rf'Sygnał trójkątny z zeropaddingiem ($N$={N2})')
axs[0, 1].set_xlabel('Czas [s]')
axs[0, 1].set_ylabel('Amplituda')
axs[0, 1].grid(True)
# Widmo dla N=32 z zaznaczeniem harmonicznych
axs[1, 0].stem(f1_spec, X1, basefmt="k-", linefmt='C1-', markerfmt='C1o')
for h in harmonics:
idx = np.argmin(np.abs(f1_spec - h))
axs[1, 0].stem(f1_spec[idx], X1[idx], linefmt='C3-', markerfmt='C3o', basefmt=" ")
axs[1, 0].set_xlim(0, fs/2)
axs[1, 0].set_title(rf'Widmo ($N=32$)')
axs[1, 0].set_xlabel('Częstotliwość [Hz]')
axs[1, 0].set_ylabel('Amplituda')
axs[1, 0].grid(True)
# Widmo dla N=128 z zaznaczeniem harmonicznych
axs[1, 1].stem(f2_spec, X2, basefmt="k-", linefmt='C1-', markerfmt='C1o')
for h in harmonics:
idx = np.argmin(np.abs(f2_spec - h))
axs[1, 1].stem(f2_spec[idx], X2[idx], linefmt='C3-', markerfmt='C3o', basefmt=" ")
axs[1, 1].set_xlim(0, fs/2)
axs[1, 1].set_title(rf'Widmo z zeropaddingiem ($N=128$)')
axs[1, 1].set_xlabel('Częstotliwość [Hz]')
axs[1, 1].set_ylabel('Amplituda')
axs[1, 1].grid(True)
plt.tight_layout()
plt.show()