4. Analiza częstotliwościowa sygnałów

4.3. Funkcje okna czasowego

W praktycznych zastosowaniach, analiza i przetwarzanie sygnałów za pomocą ciągłej transformaty Fouriera napotyka istotne ograniczenie – nie jest możliwe całkowanie od \(-\infty\) do \(+\infty\), jak zakłada definicja transformaty. W rzeczywistości sygnał \(x(t)\) można obserwować lub przetwarzać tylko w ograniczonym przedziale czasu, np. od pewnej chwili \(t_0\) do \(t_0 + T\). Jest to równoznaczne z analizą fragmentu sygnału:

\( x_w(t) = x(t) \cdot w(t) \)

gdzie \( w(t) \) jest funkcją okna czasowego, zwykle prostokątnego, przyjmującą wartość \(1\) w przedziale \([t_0, t_0 + T]\) i \(0\) poza nim. Ma to bezpośredni wpływ na wynikową transformatę Fouriera, ponieważ zgodnie z właściwością iloczynu:

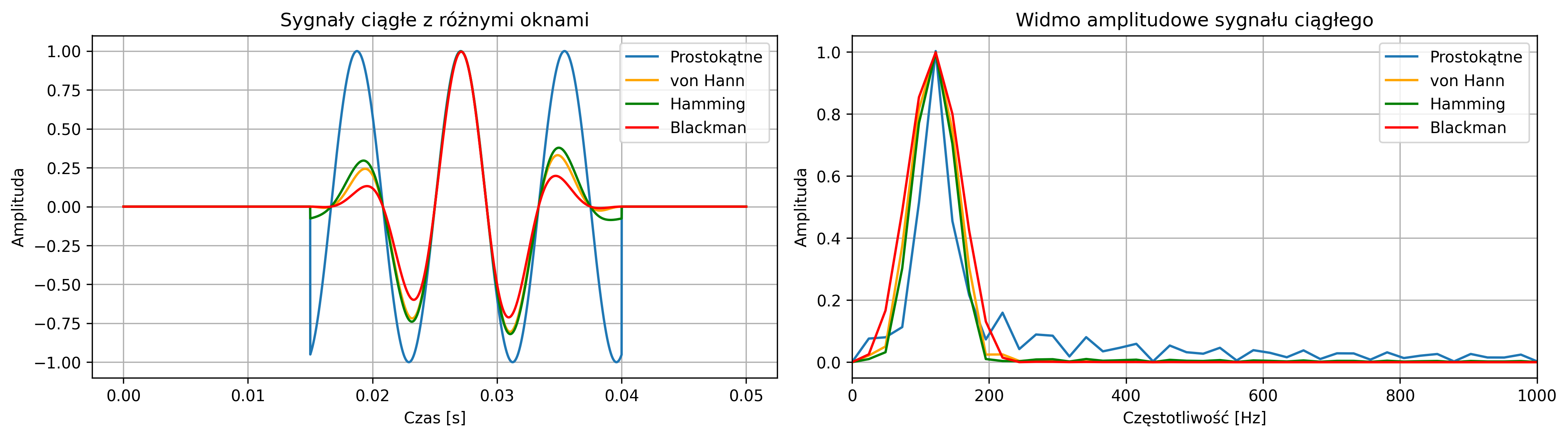
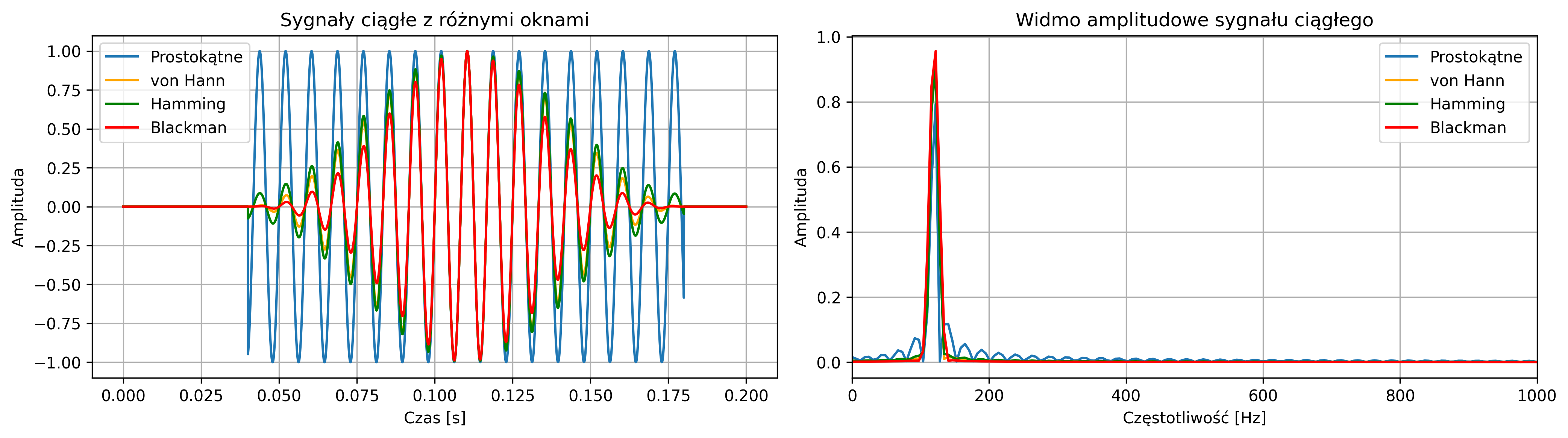
\( \mathcal{F}[x(t)\cdot w(t)] = X(\omega) \ast W(\omega) \)

Widmo sygnału zostaje przekształcone przez splot z widmem funkcji okna. Jeśli analizujemy ograniczony w czasie fragment sygnału, to w rzeczywistości widzimy widmo nie oryginalnego sygnału, ale jego wersję przemnożoną przez funkcję okna. Z tego powodu właściwości częstotliwościowe funkcji okna są kluczowe dla jakości analizy widmowej.

Przypomnijmy, że splot z deltą Diraca pozostawia sygnał bez zmian:

\( X(\omega) \ast \delta(\omega) = X(\omega) \)

Jeśli \( W(\omega) \) byłoby idealną deltą Diraca, to wymnażanie sygnału przez funkcję okna nie wpływałoby na jego widmo – otrzymalibyśmy dokładnie to samo widmo, jak w przypadku sygnału nieskończonego. W praktyce widmo funkcji okna nie może być deltą Diraca, gdyż funkcje o nieskończenie wąskim widmie mają nieskończenie długi przebieg czasowy. Dlatego też dążymy do tego, aby widmo funkcji okna \( W(\omega) \) było jak najbardziej zbliżone do delty Diraca:

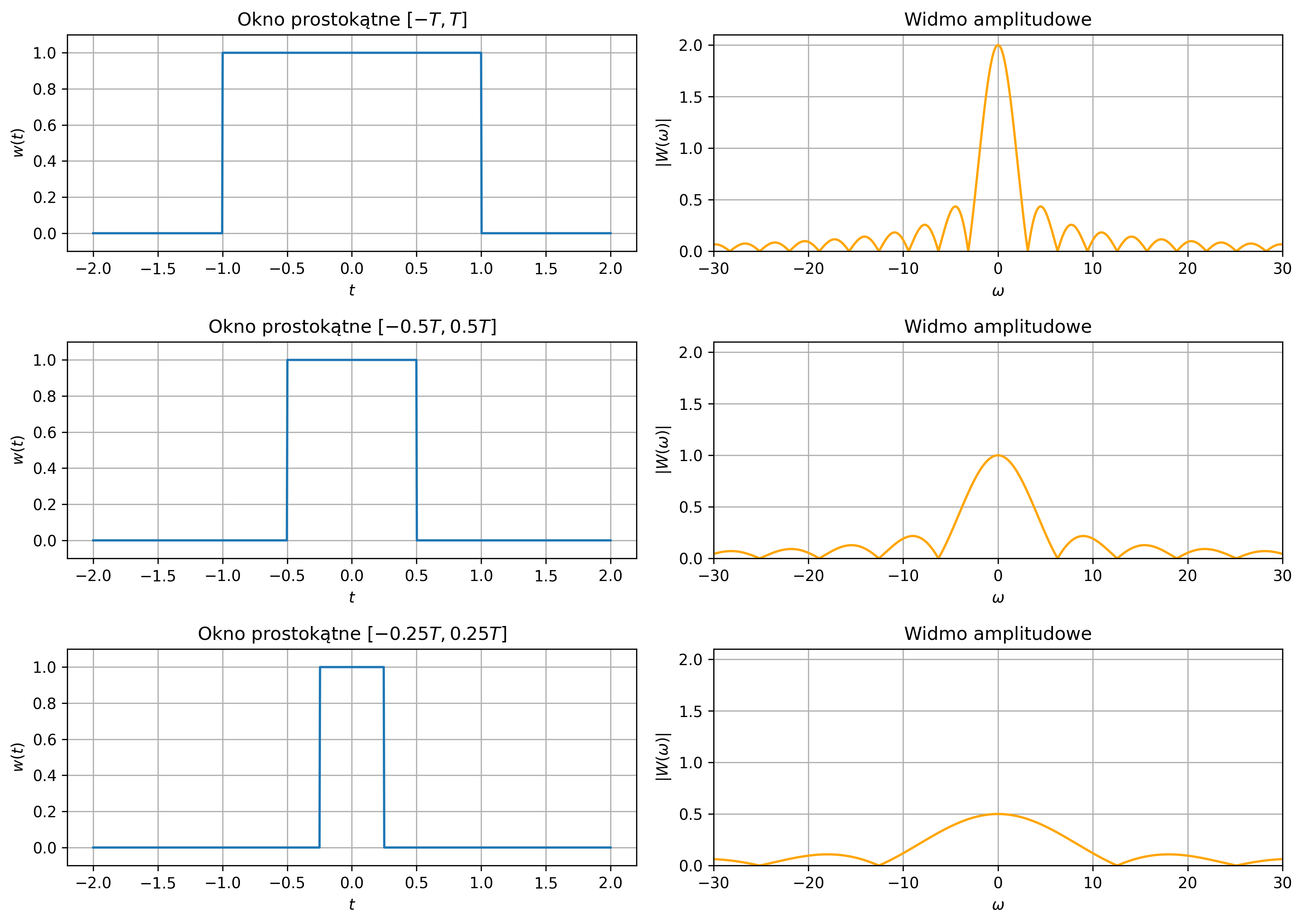
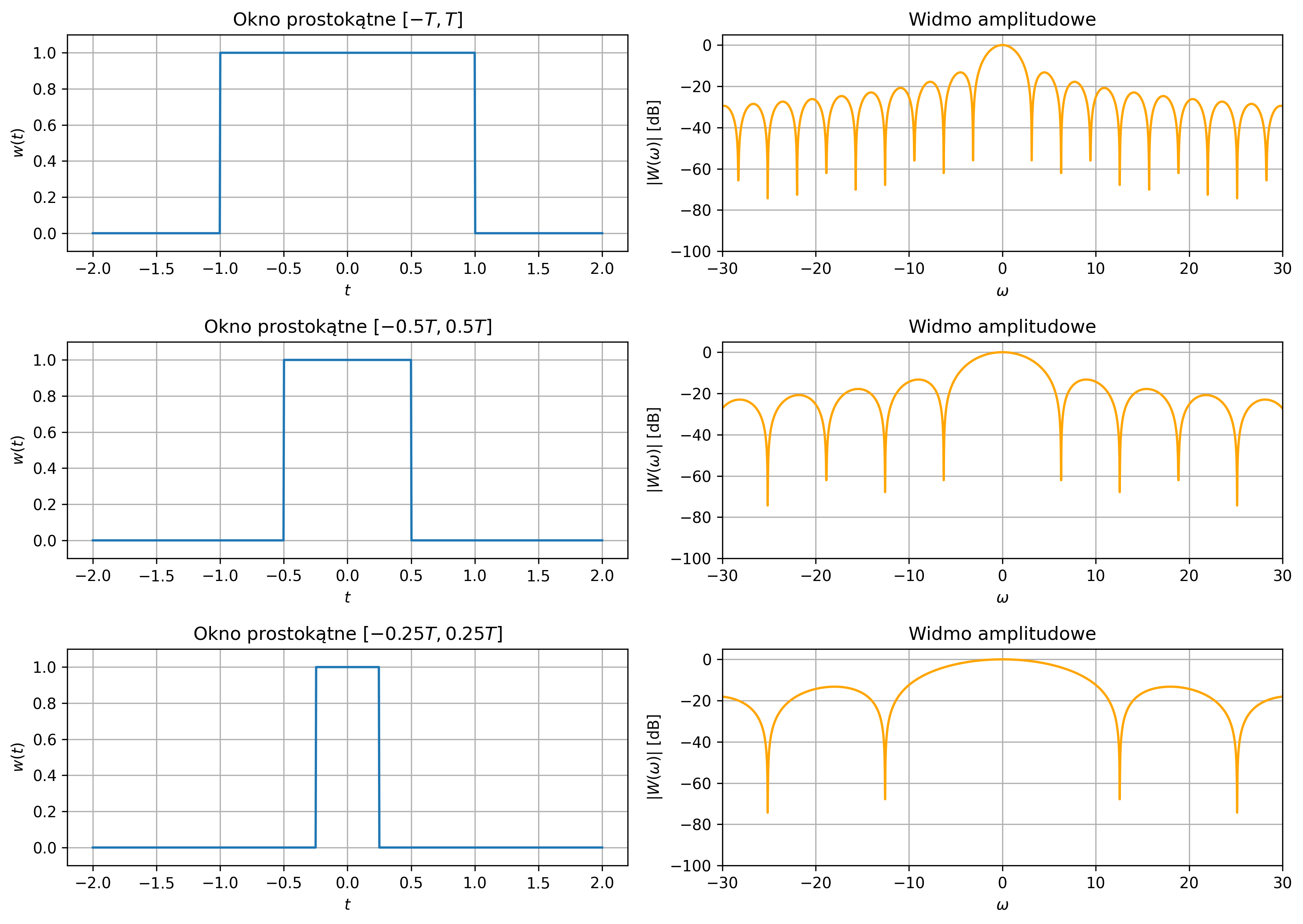
  • maksymalnie skoncentrowane wokół \(\omega = 0\),
  • szybko malejące do zera przy oddalaniu się od tej pulsacji,
  • z wąskim listkiem głównym i niskim poziomem listków bocznych (oscylacji po obu stronach).

Zaznaczmy, że ze względu na zasadę nieoznaczoności nie jest możliwe jednoczesne osiągnięcie bardzo wąskiego listka głównego oraz bardzo silnego tłumienia listków bocznych. Każde okno stanowi zatem kompromis między:

  • rozdzielczością częstotliwościową – jak dobrze można odróżnić bliskie składowe,
  • a tłumieniem zakłóceń widmowych – jak bardzo „przecieka” energia do sąsiednich częstotliwości.

Wpływ szerokości okna prostokątnego na widmo amplitudowe został pokazany na rys. 4.11. W celu pokazania większych szczegółów otrzymanych widm amplitudowych, zamiast skali liniowej zastosowano skalę decybelową. Różnicę można zaobserwować na rys. 4.12, co raz jeszcze potwierdza słuszność wykorzystywania tej skali.

Rys. 4.11. Wykres okien prostokątnych i ich widm amplitudowych w skali liniowej
 
 
Rys. 4.12. Wykres okien prostokątnych i ich widm amplitudowych w skali decybelowej
 
Rys. 4.11 i 4.12 są bezpośrednią ilustracją zasady nieoznaczoności. Im szersze okno prostokątne w czasie, tym węższe i bardziej skupione widmo. Analogicznie, im węższe okno, tym szersze widmo z większym rozmyciem i bocznymi listkami.
 
Oprócz funkcji okna prostokątnego, w praktyce stosuje się również inne funkcje okien, takie jak okno Hanninga (von Hanna), Hamminga, Blackmana, Gaussa czy Kaisera. Zostały one zaprojektowane w celu zmniejszenia niepożądanych efektów ubocznych okna prostokątnego, takich jak wysoki poziom listków bocznych w widmie.
 
Kompromis między szerokością listka głównego a tłumieniem listków bocznych w zależności od wykorzystanej funkcji został zilustrowany na rys. 4.13. Okna wygładzające, jak Hanninga czy Blackmana, mają łagodniejszy przebieg na brzegach, co skutkuje niższym poziomem listków bocznych w widmie. W rezultacie umożliwiają lepsze tłumienie sygnałów o częstotliwościach leżących poza pasmem głównym, kosztem nieco szerszego listka głównego.
 
Rys. 4.13. Wykres funkcji okien i ich widm amplitudowych
 
W zastosowaniach, gdzie istotne jest dobre rozdzielanie blisko leżących składowych częstotliwościowych, preferowane są okna o wąskim listku głównym (np. Hamming). W sytuacjach wymagających dużego tłumienia składowych poza pasmem, korzystniejsze są okna o niskim poziomie listków bocznych, jak np. Blackmana.
 
Zobaczmy teraz, jak od kształtu \( W(\omega) \) zależy wielkość „deformacji” widma \( X(\omega) \). Na rysunku 4.14 i 4.15 przedstawiono graficzną ilustrację rozważanej sytuacji. Sygnał sinusoidalny o częstotliwości \(120\) Hz jest mnożony przez okno prostokątne, Hanninga, Hamminga i Blackmana o dwóch szerokościach – większej i mniejszej.
 
Rys. 4.14. Wykresy sygnału sinusoidalnego z nałożonymi oknami i ich widm amplitudowych
 
Rys. 4.15. Wykresy sygnału sinusoidalnego z nałożonymi oknami i ich widm amplitudowych
 
Im dłuższy czas trwania sygnału, tym widmo amplitudowe swoim kształtem przybliża się do widma delty Diraca. Widać, jak różne okna wpływają na rozmycie i wysokość prążków. Zauważmy, że pomimo tego, iż przedstawiony sygnał jest okresowy, jego widmo amplitudowe nie przedstawia jednego prążka w \(120\) Hz. Zjawisko to nazywa się przeciekiem i zostanie omówione w rozdziale 4.6 w odniesieniu do dyskretnej transformaty Fouriera.