Podręcznik

W praktycznych zastosowaniach analizy częstotliwościowej nie mamy dostępu do sygnału ciągłego \( x(t) \), lecz jedynie do jego wersji dyskretnej – zbioru próbek \( x[n] \), otrzymanych w wyniku próbkowania sygnału analogowego w dziedzinie czasu oraz skwantowania jego amplitudy za pomocą przetwornika analogowo-cyfrowego. Przetwarzanie odbywa się więc na dyskretnym ciągu wartości, a nie na funkcji ciągłej.

Dyskretna transformata Fouriera (DFT) to procedura matematyczna umożliwiająca wyznaczenie składowych częstotliwościowych sygnału dyskretnego o skończonej długości. DFT stanowi wynik kolejnych przekształceń:

W wyniku tych kroków przechodzimy od całkowego przekształcenia ciągłego do postaci dyskretnej, otrzymując wzór na dyskretną transformatę Fouriera:

\( X[k] = \sum_{n=0}^{N-1} x[n] e^{-j k \left(\frac{2\pi}{N}\right) n}, \quad k = 0,1,\ldots, N-1 \)

gdzie:

• \( k \) – numer harmonicznej,
• \( n \) – numer próbki,
• \( N \) – liczba próbek,
• \( T \) – okres próbkowania,
• \( f_s \) – częstotliwość próbkowania.

Zakładamy, że sygnał ciągły i okresowy \( x(t) \), o okresie \( T \), został spróbkowany \( N \) razy w jednym okresie, w chwilach \( t_n = n \cdot T / N \). Próbkowanie odbywa się zgodnie z twierdzeniem Nyquista–Shannona, czyli z częstotliwością próbkowania:

\( f_s = \frac{N}{T} \)

która jest co najmniej dwa razy większa od najwyższej częstotliwości zawartej w sygnale:

\( f_s \geq 2 f_{\max} \)

W przypadku sygnałów okresowych wystarczy spróbkować jeden okres sygnału, aby za pomocą DFT wyznaczyć jego widmo. Jeśli próbkowanie spełnia warunek Nyquista, to DFT dostarcza pełnej informacji o składnikach harmonicznych sygnału.

Odwrotna dyskretna transformata Fouriera (IDFT) wyraża się wzorem:

\( x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] e^{j k \left(\frac{2\pi}{N}\right) n} \)

DFT i IDFT tworzą parę odwrotną – jeśli zastosujemy DFT, a następnie IDFT, odzyskamy sygnał \( x[n] \). Niektórzy autorzy przenoszą dzielenie przez \( N \) do równania na \( X[k] \).

Widmo DFT to zbiór \( N \) współczynników \( X[k] \), które reprezentują zawartość częstotliwościową sygnału dyskretnego \( x[n] \). Dlatego każdy współczynnik \( X[k] \) określa:

• amplitudę \( |X[k]| \),
• fazę \( \arg X[k] \),

składowej sinusoidalnej o częstotliwości:

\( f_k = \frac{k}{N} f_s, \quad k = 0,1,\ldots, N-1 \)

Dyskretna transformata Fouriera ma wiele ważnych własności, które są analogiczne do tych znanych z ciągłej transformaty Fouriera, ale z uwagi na dyskretną i skończoną naturę sygnałów DFT, przyjmują one specyficzne formy. Do najważniejszych można zaliczyć:

• symetrię dla sygnałów rzeczywistych – próbki widma położone symetrycznie są parami sprzężone,
• okresowość – widmo DFT jest okresowe z okresem \( N \),
• liniowość – DFT jest przekształceniem liniowym, tzn. przekształcenie kombinacji liniowej sygnałów jest taką samą kombinacją liniową ich widm.

Z własności symetrii widma wynika, że jeśli sygnał \( N \)-okresowy jest rzeczywisty, a liczba jego próbek jest parzysta, to całe widmo jest w pełni określone przez \( \frac{N}{2} + 1 \) wartości:

• dwie wartości rzeczywiste: \( X[0] \) oraz \( X\left[\frac{N}{2}\right] \),
• oraz \( \frac{N}{2} - 1 \) wartości zespolonych: \( X[1], X[2], \ldots, X\left[\frac{N}{2} - 1\right] \).

Stąd użyteczna informacja jest zawarta tylko w pierwszych \( \frac{N}{2} + 1 \) prążkach.

Na rys. 4.16 pokazane zostały wykresy widma amplitudowego i fazowego dla pewnego sygnału. Ponieważ jest to sygnał rzeczywisty, połowa widma to sprzężone odbicie lewej połowy – dlatego widzimy prążki symetryczne parami. Prążków jest niewiele, ale o wyraźnej amplitudzie (reszta jest zerowa), a także ich fazy mają wartości 0 – możemy przypuszczać, że sygnał jest sumą kilku funkcji harmonicznych.

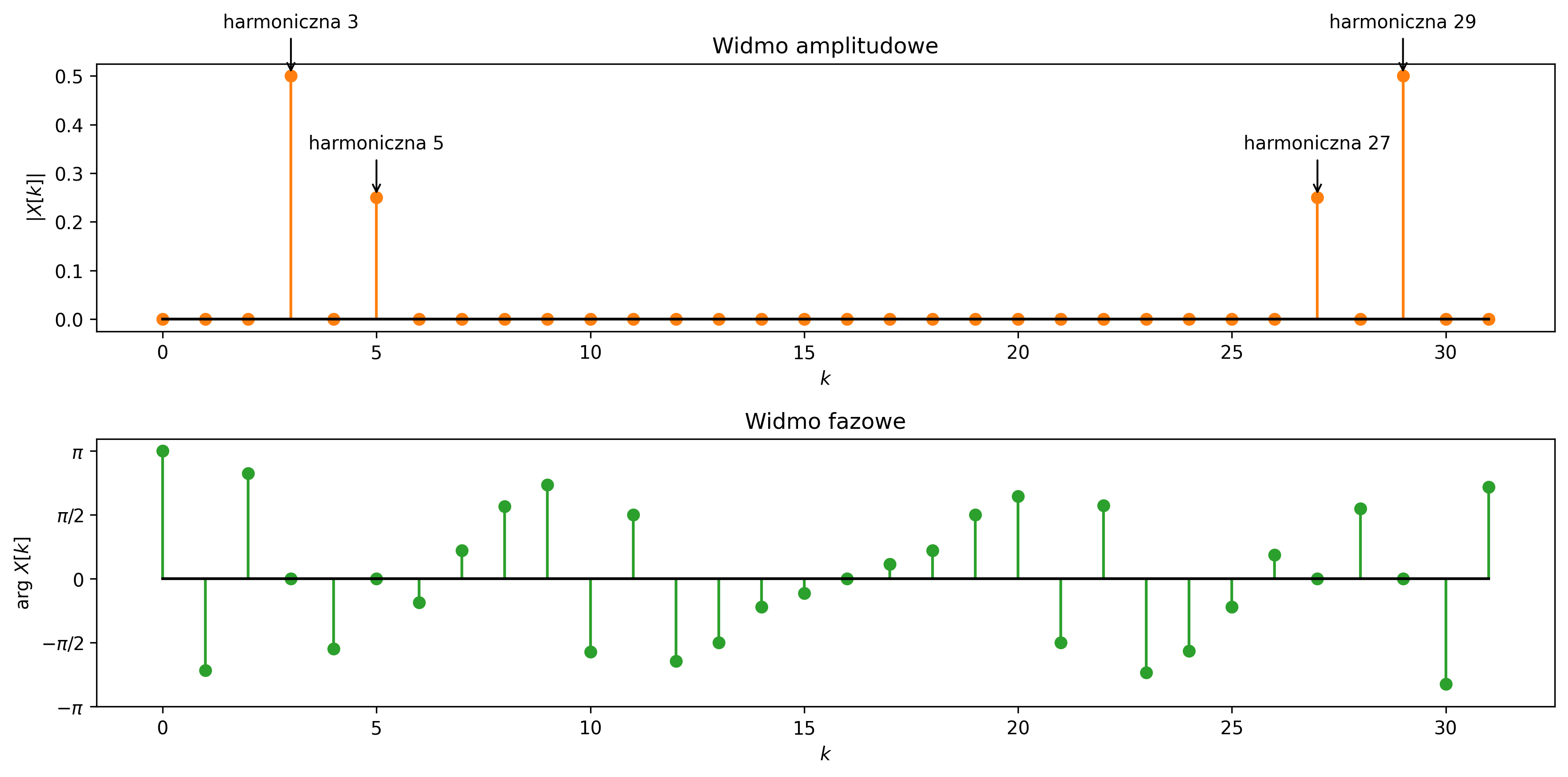
Należy zaznaczyć, że każdy z tych prążków zawiera połowę amplitudy składowej sygnału. Zatem suma amplitud prążków symetrycznych daje rzeczywistą amplitudę składowych sinusoidalnych. Każdy prążek widma wskazuje na obecność składowej o częstotliwości i amplitudzie:

• prążki w \( k = 3 \) i \( k = 29 \) wskazują obecność składowych o \(3\) i \(29\) jednostkach częstotliwości, które mają wysokość \( \approx 0.5 \),
• prążki w \( k = 5 \) i \( k = 27 \) wskazują obecność składowych o \(5\) i \(27\) jednostkach częstotliwości, które mają wysokość \( \approx 0.25 \).

Stąd, aby odtworzyć wzór sygnału z wykresu DFT dla okresu \( N = 32 \), musimy jeszcze obliczyć częstotliwość w zależności od pozycji prążka. Na podstawie wykresu nie możemy tym prążkom przypisać konkretnych częstotliwości, jeśli nie znamy odgórnie częstotliwości próbkowania. Dlatego często przyjmuje się roboczo \( f_s = N \), żeby łatwo przekształcać indeksy prążków na ich częstotliwości:

\( f_k = \frac{k}{N} \cdot f_s = \frac{k}{32} \cdot 32 = k \)

Wtedy indeks \( k \) bezpośrednio odpowiada częstotliwości \( f_k \). Zatem:

\( f_3 = 3 \,\text{Hz} \) oraz \( f_5 = 5 \,\text{Hz} \).

Z wykresu fazowego możemy odczytać, że dla:

• \( k = 3 \) i \( k = 5 \) faza wynosi \(0\),

co sugeruje, że sygnał, który widzimy, jest sumą kosinusów (faza może wynosić \(0\) lub \( \pi \)). W przypadku, gdyby faza wynosiła \( -\frac{\pi}{2} \) lub \( \frac{\pi}{2} \), mielibyśmy do czynienia z sumą sinusów. Stąd wzór sygnału w dziedzinie czasu będzie w postaci:

\( x(n) \approx A_1 \cos\left( 2\pi f_1 t_n \right) + A_2 \cos\left( 2\pi f_2 t_n \right) \)

Po spróbkowaniu sygnału z częstotliwością \( f_s = N \), otrzymamy:

\( t_n = n \cdot \frac{T}{N} = \frac{n}{f_s} = \frac{n}{N} \)

a stąd:

\( x[n] \approx A_1 \cos\left( 2\pi f_1 \frac{n}{f_s} \right) + A_2 \cos\left( 2\pi f_2 \frac{n}{f_s} \right) \)

Skoro zakładamy, że mamy \( N \) próbek DFT, a częstotliwości odpowiadają wartościom indeksów \( k = 1,2,\ldots, N-1 \), wzór, którego szukamy, wygląda następująco:

\( x[n] \approx A_1 \cos\left( 2\pi f_3 \frac{n}{f_s} \right) + A_2 \cos\left( 2\pi f_5 \frac{n}{f_s} \right) \)

Ostatecznie sygnał jest w przybliżeniu postaci:

\( x[n] \approx 1 \cdot \cos\left( 2\pi \cdot 3 \frac{n}{32} \right) + \frac{1}{2} \cos\left( 2\pi \cdot 5 \frac{n}{32} \right) \)

Z rys. 4.16 wynika wniosek, że jeśli sygnał jest sumą kilku funkcji harmonicznych, to DFT pozwala je zidentyfikować – ich amplitudę, częstotliwość i fazę.

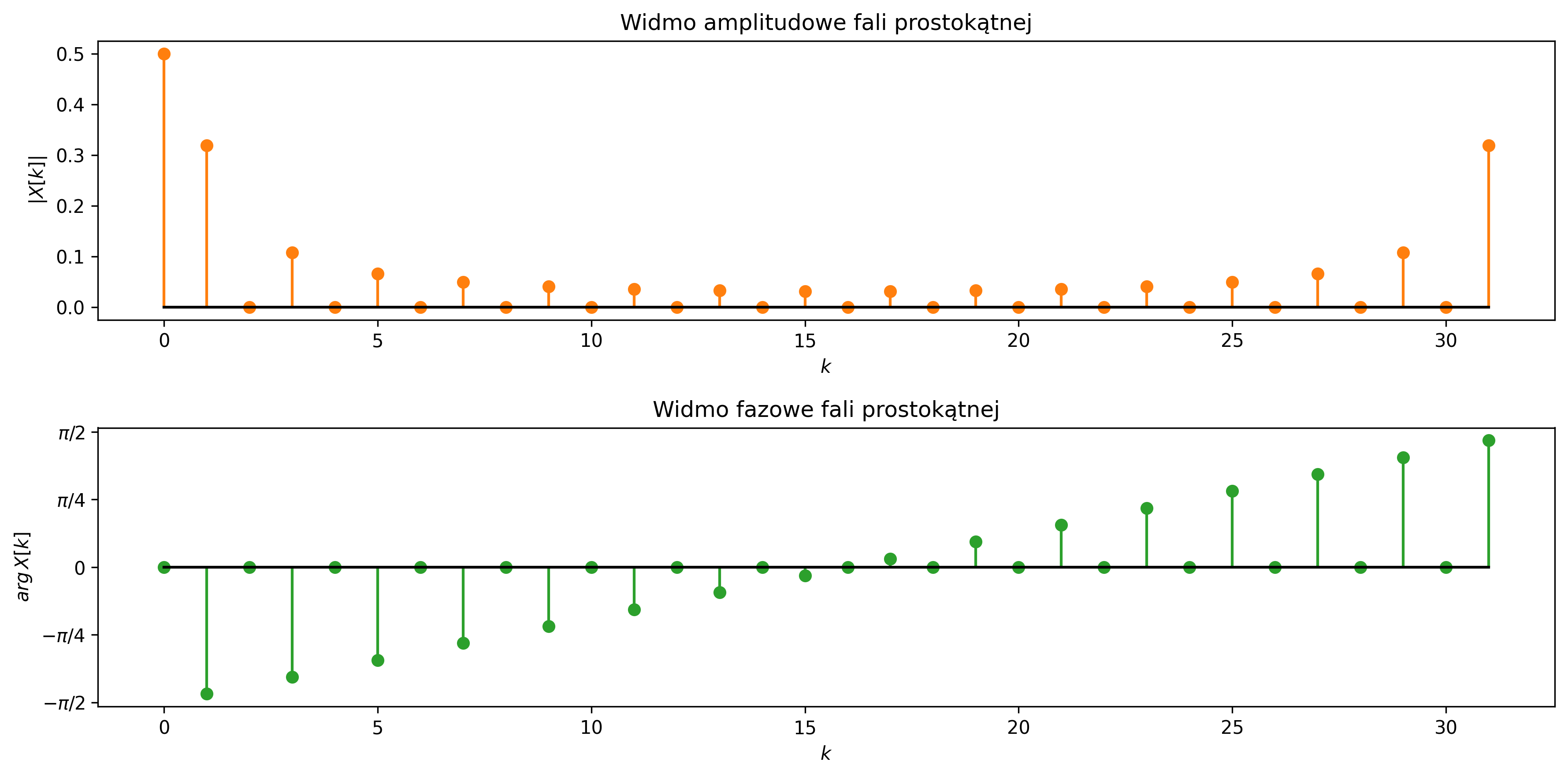
W przypadku sygnałów bardziej złożonych, np. sygnału prostokątnego (rys. 4.17), widmo będzie zawierać harmoniczne wyższych rzędów i możemy odtworzyć tylko jego przybliżoną postać przez odwrotną DFT.

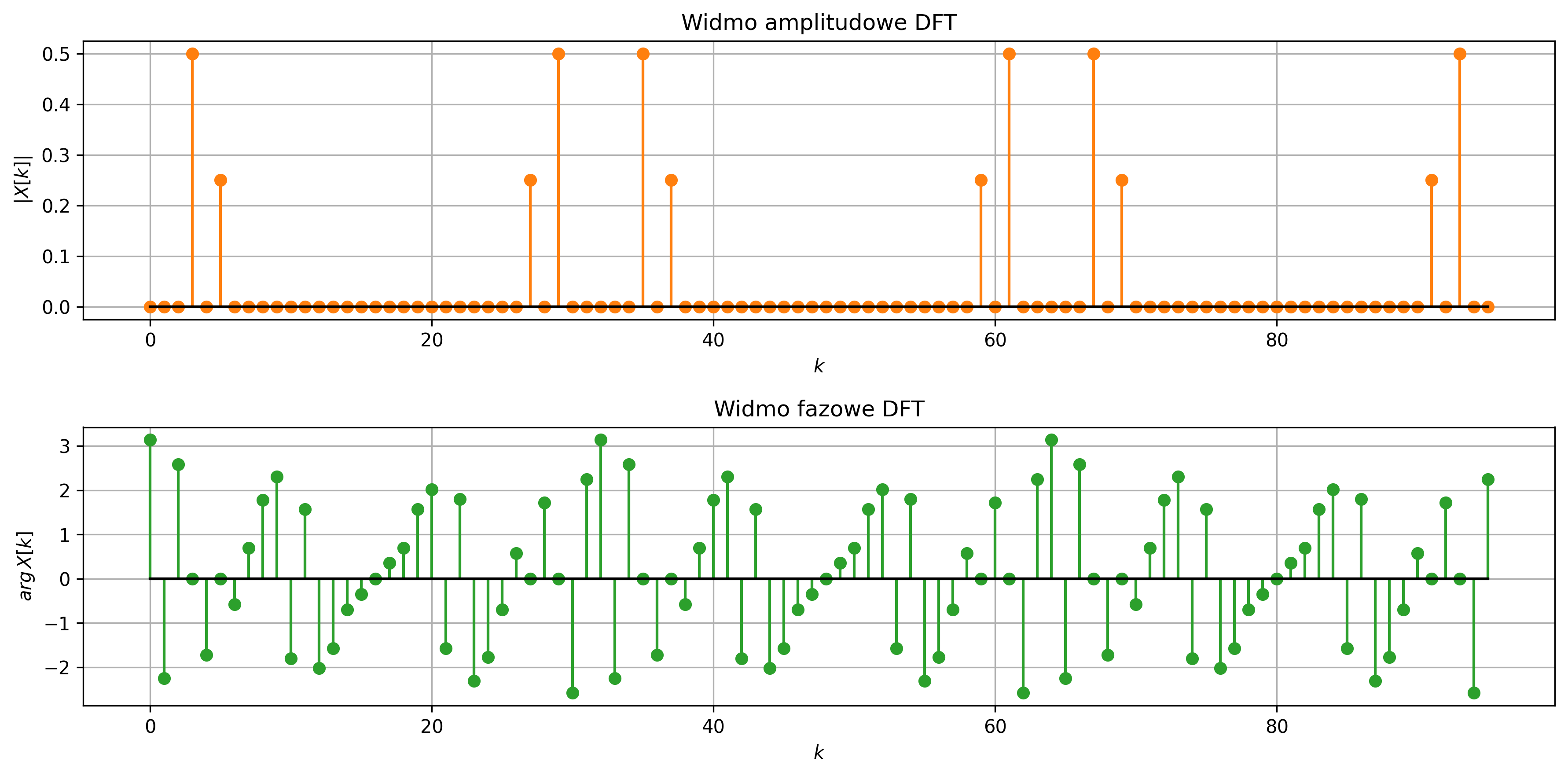
Rozdzielczość częstotliwościowa określa, jak blisko siebie mogą być dwie składowe częstotliwościowe, aby DFT była w stanie je rozróżnić:

\( \Delta f = \frac{f_s}{N} \)

gdzie \( f_s \) jest częstotliwością próbkowania, a \( N \) rozmiarem DFT. Większa wartość \( N \) to lepsza rozdzielczość częstotliwościowa – możemy wykryć subtelne różnice między częstotliwościami w sygnale. Przy zbyt małym \( N \), składowe sygnału położone blisko siebie mogą zlać się w jedno maksimum.

Rozdzielczość czasowa wiąże się z długością analizowanego fragmentu sygnału i jest to minimalny odstęp czasowy pomiędzy dwoma zdarzeniami w sygnale, który umożliwia ich rozróżnienie:

\( \Delta t = \frac{N}{f_s} \)

Dłuższy czas analizy – większe \( N \) – oznacza gorszą rozdzielczość czasową: tracimy informację o tym, kiedy dokładnie w sygnale nastąpiło dane zdarzenie. Jeżeli dwa impulsy w sygnale wystąpią w odstępie mniejszym niż \( \Delta t \), to przy analizie DFT z odcinka zawierającego oba impulsy zostaną one potraktowane jako jedno zdarzenie. W efekcie informacje o ich dokładnym czasie wystąpienia zostaną utracone.

Dlatego w analizie DFT mamy wyraźny kompromis między rozdzielczością czasową i częstotliwościową. Ten kompromis jest szczególnie widoczny w analizie sygnałów zmiennych w czasie, gdzie trzeba balansować między dokładnością czasową a częstotliwościową.