Podręcznik

W analizie częstotliwościowej, przedstawiamy widmo amplitudowe, czyli moduł transformaty Fouriera sygnału. W analizie sygnałów losowych lub sygnałów z szumem bardziej istotna jest widmowa gęstość mocy (PSD, ang. Power Spectral Density).

Zgodnie z twierdzeniem Wienera-Chinczyna, dla procesu losowego \( X(t) \), który jest stacjonarny w szerokim sensie, gęstość widmowa mocy jest transformatą Fouriera funkcji autokorelacji:

gdzie \( f \) jest częstotliwością wyrażoną w hercach oraz \( R_{XX}(\tau)=E[X(t)X(t+\tau)] \) Odwrotny związek w dziedzinie czasu jest postaci:

Zaznaczmy, że stacjonarność procesu gwarantuje, że gęstość widmowa mocy istnieje i ma jednoznaczny związek z funkcją autokorelacji – funkcja autokorelacji i gęstość widmowej mocy tworzą parę transformat Fouriera. Oznacza to, że znajomość autokorelacji pozwala wyznaczyć gęstość widmową mocy, która opisuje rozkład mocy sygnału w dziedzinie częstotliwości. W ten sposób przechodzimy od charakterystyki procesu w dziedzinie czasu do opisu w dziedzinie częstotliwości.

Dzięki funkcji autokorelacji możemy ocenić, czy proces „pamięta” swoje przeszłe wartości i jak długo utrzymują się zależności między próbkami sygnału. Z kolei gęstość widmowa mocy pokazuje, jak ta „pamięć” i korelacje w czasie przekładają się na obecność określonych częstotliwości w sygnale, czyli jak moc średnia procesu rozkłada się pomiędzy poszczególne składowe częstotliwościowe.

Dla ciągłych, stacjonarnych procesów ergodycznych średnia po wszystkich realizacjach może być zastąpiona średnią po czasie, co prowadzi do praktycznej definicji PSD jako periodogramu:

gdzie \( x(t) \) jest pojedynczą realizacją procesu, \( E[] \) oznacza wartość oczekiwaną, \( X_T(f) \) jest transformatą Fouriera fragmentu sygnału z przedziału czasowego \( [-T, T] \) (o długości \( 2T \)):

oraz \( X_T^{\ast\mathstrut}(f) \) jest sprzężeniem zespolonym tej transformaty. Dla rzeczywistych procesów ergodycznych wartość oczekiwaną można zastąpić średnią po czasie jednej realizacji, co daje oszacowanie PSD w postaci:

Obliczenie periodogramu sprowadza się to do wyznaczenia kwadratu modułu widma i przedstawia zatem rozkład mocy sygnału w funkcji częstotliwości.

PSD wyrażana jest zazwyczaj w jednostkach mocy na jednostkę częstotliwości, np. w \( \textrm{W}/\textrm{Hz} \), \( \textrm{V}^2/\textrm{Hz} \), co oznacza moc przypadającą na jednostkę szerokości pasma częstotliwości. W przypadku reprezentacji logarytmicznej stosuje się jednostkę \( \textrm{dB}/\textrm{Hz} \), określającą moc w decybelach na jednostkę częstotliwości. Umożliwia to porównywanie mocy różnych składowych częstotliwościowych, szczególnie przydatne w przypadku szumów, zakłóceń i analizy statystycznej sygnałów niestacjonarnych.

Dla procesu dyskretnego \( X[n] \), otrzymanego w wyniku próbkowania procesu ciągłego \( X(t) \) z okresem próbkowania \( T \), definicję teoretycznej gęstości widmowej mocy można zapisać jako:

gdzie \( X_N(f) \) jest dyskretną transformatą Fouriera (DTF) fragmentu sygnału \( x[n] \) o długości \( N \) próbek:

W praktyce, dla jednej realizacji procesu ergodycznego, wartość oczekiwaną można zastąpić średnią po czasie, a estymator gęstości widmowej mocy przyjmuje postać periodogramu:

Ponieważ obliczenia w praktyce wykonuje się dla dyskretnych częstotliwości \( f_k=\frac{k}{N T} \) estymator można zapisać w postaci dyskretnej transformaty Fouriera (DFT):

Na rys. 5.14 przedstawiono estymowaną gęstość widmową mocy (PSD) sygnału, obliczoną metodą periodogramu. W analizie wykorzystano sygnał losowy złożony z dwóch składowych sinusoidalnych o częstotliwościach \(50\) Hz oraz \(200\) Hz, na który nałożono szum biały o niewielkiej mocy:

gdzie \( w(t) \) jest szumem białym o rozkładzie \( N(0,\sigma^2) \). Sygnał został spróbkowany z częstotliwością \( f_s=1000 \) Hz, a długość sygnału \( N = 1024 \) próbek. Analiza widma pozwala ocenić, jak energia (lub moc) sygnału rozkłada się w dziedzinie częstotliwości.

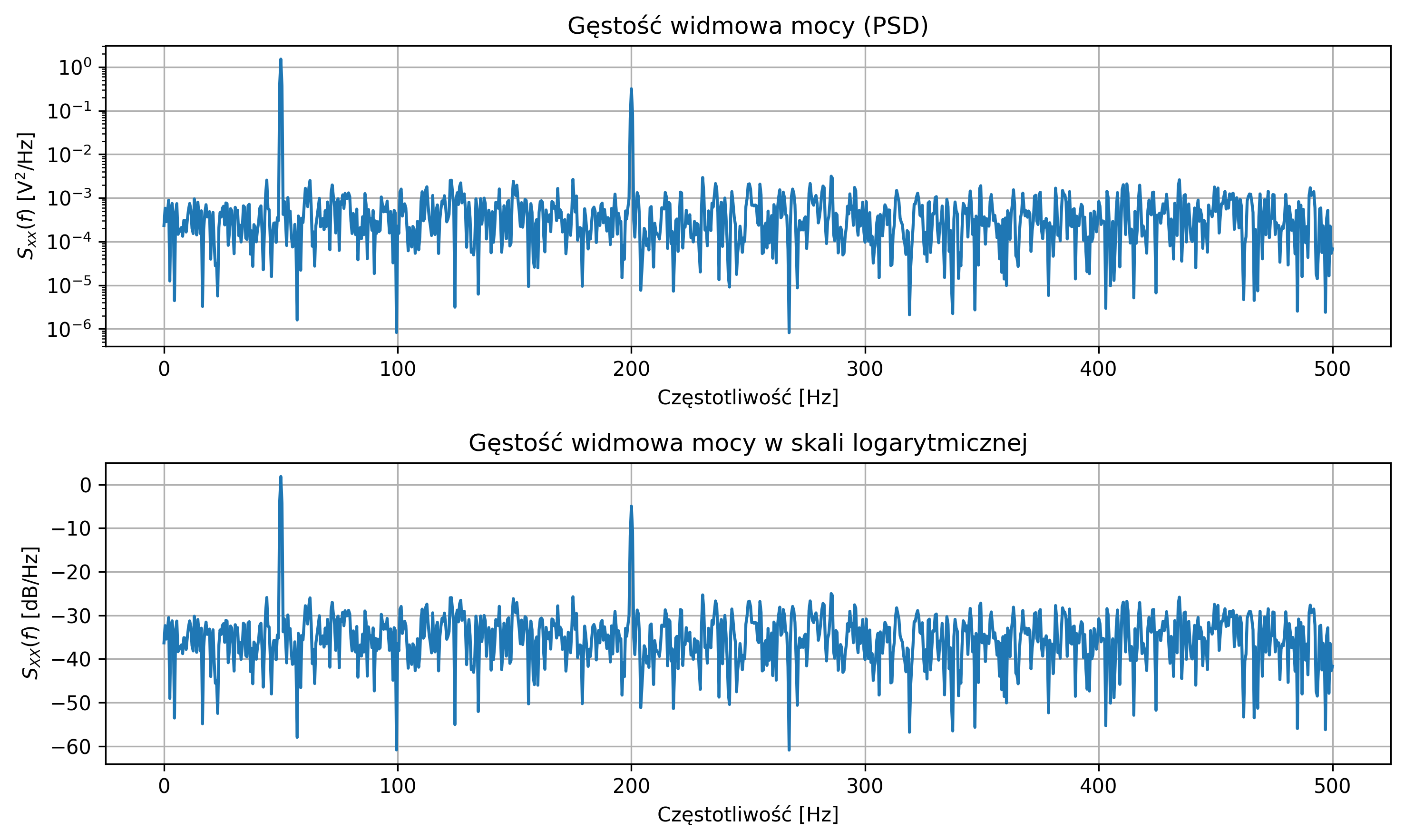
Na górnym wykresie PSD wyrażono w jednostkach liniowych \( \textrm{V}^2/\textrm{Hz} \). Widać wyraźnie dwa lokalne maksima (piki) odpowiadające częstotliwościom \(50\) Hz oraz \(200\) Hz, które odpowiadają składowym sinusoidalnym obecnym w sygnale. Szerokość i wysokość tych pików zależy od długości obserwacji i okna analizy – dłuższy sygnał daje lepszą rozdzielczość częstotliwościową.

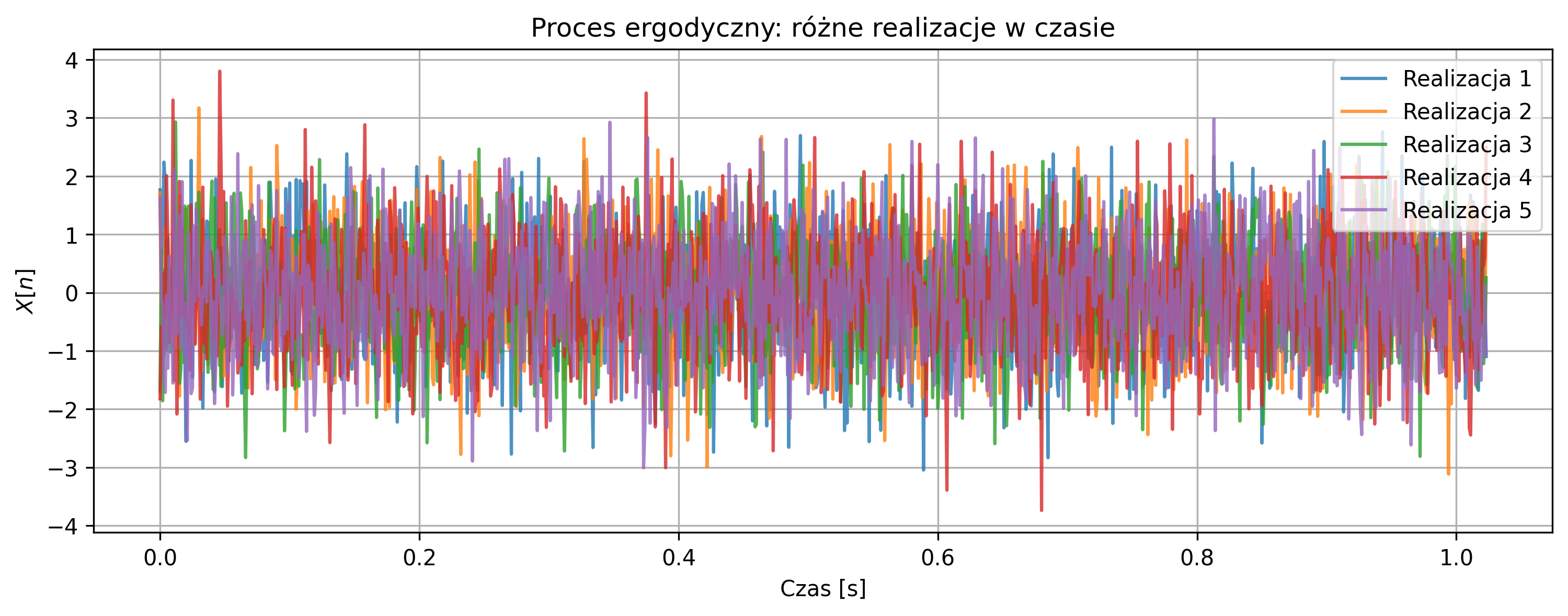
Na rysunku 5.15 przedstawiono pięć niezależnych realizacji procesu ergodycznego w czasie. Każda realizacja ma podobny przebieg – sygnał oscyluje wokół zera, a średnia wartość po czasie jest zbliżona do zera. Widoczne jest, że wszystkie realizacje mają podobny charakter losowy, co oznacza, że statystyki procesu (średnia, wariancja) są takie same niezależnie od wybranej realizacji. Oznacza to, że średnia po czasie jest równa średniej po realizacjach, a proces można uznać za ergodyczny.

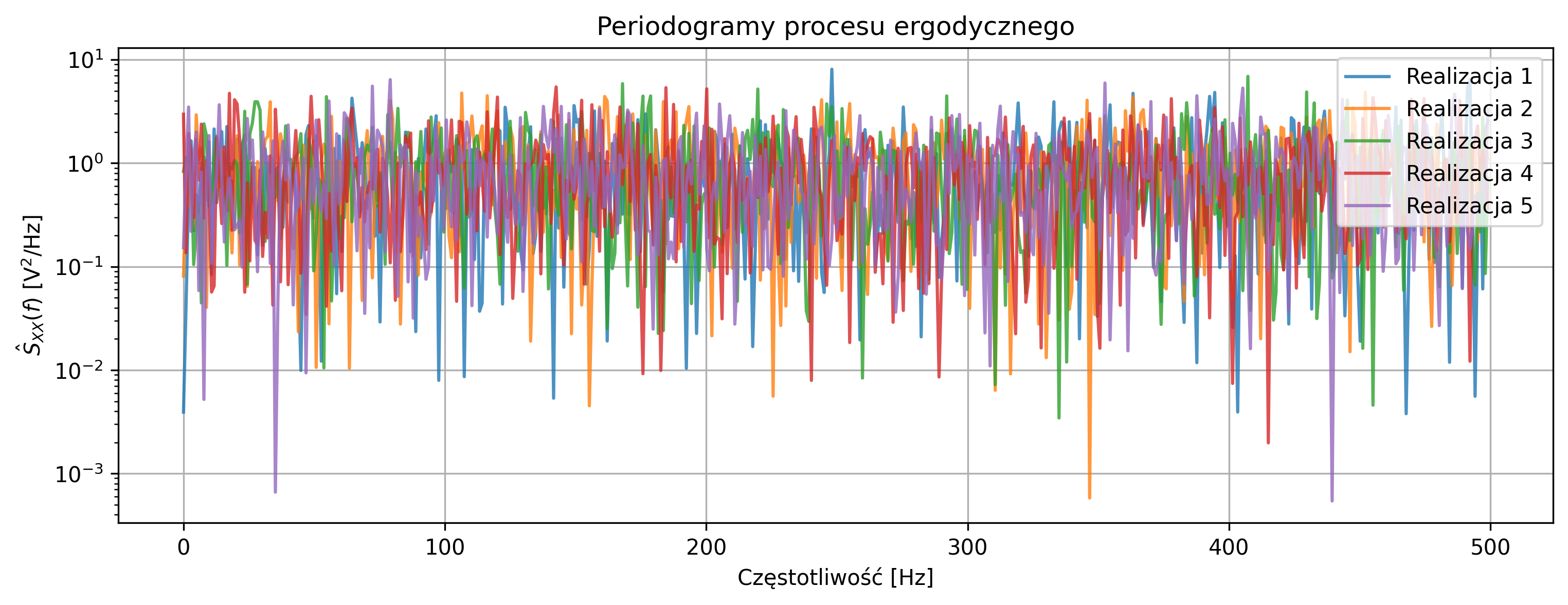
Wykresy periodogramów (oszacowania gęstości widmowej mocy), odpowiadających powyższym realizacjom w czasie, zilustrowano na rysunku 5.16. Widma poszczególnych przebiegów są do siebie podobne i nie zawierają dominującej składowej przy \( f=0 \). Moc jest rozłożona równomiernie w paśmie częstotliwości, co potwierdza stacjonarność i ergodyczność procesu.

Rozważmy teraz proces losowy zdefiniowany jako

gdzie \( A \) jest losową stałą o rozkładzie \( A \sim N(0,1) \), a \( w[n] \) oznacza biały szum o zerowej wartości oczekiwanej i wariancji \( \sigma_w^2 = 0.01 \). Proces ten jest stacjonarny, gdyż jego własności statystyczne nie zależą od przesunięcia w czasie, jednak nie jest ergodyczny względem wartości średniej, ponieważ każda realizacja ma inne przesunięcie poziomu średniego wynikające z losowej wartości \( A \).

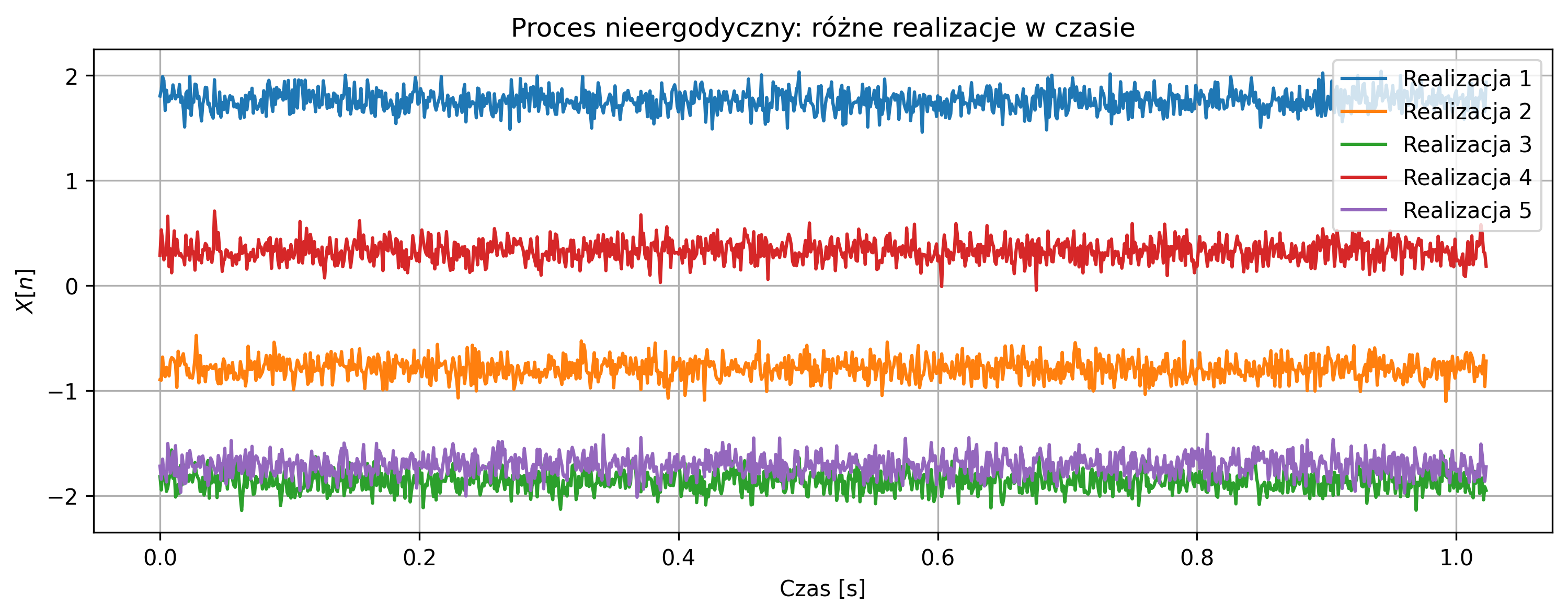
Na rys. 5.17 przedstawiono kilka realizacji tego procesu. Widać, że choć mają podobną strukturę szumową, różnią się poziomem średnim. Oznacza to, że estymacja wartości oczekiwanej na podstawie jednej realizacji nie oddaje rzeczywistej wartości średniej całego procesu. Proces nie jest ergodyczny.

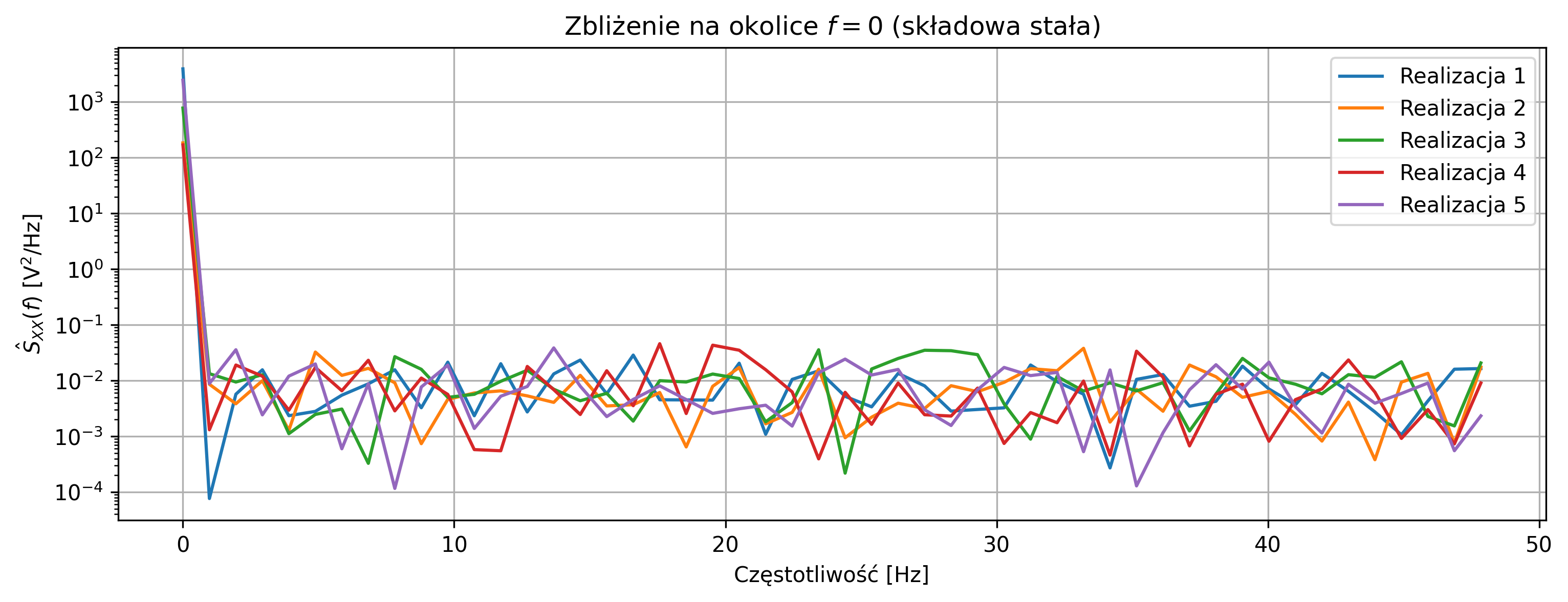
Ponieważ każda realizacja ma inną wartość składowej stałej \( A \), widmo w okolicach częstotliwości \( f=0 \) Hz (składowej stałej) znacząco różni się między realizacjami (rys. 5.18) – powoduje ona bardzo silną koncentrację energii przy częstotliwości \(0\), a wielkość tego piku różni się między realizacjami, bo różna jest wartość \( A^2 \). Widma w pozostałych częstotliwościach są podobne, ponieważ wynikają z białego szumu \( w[n] \). Krzywe periodogramów nie nachodzą na siebie tak regularnie jak w procesie ergodycznym, widmo nie jest stabilne statystycznie – nie da się przewidzieć jednej typowej postaci PSD.

W praktyce obliczeniowej klasyczny periodogram charakteryzuje się dużą wariancją, szczególnie w przypadku procesów losowych, takich jak analizowany proces nieergodyczny. Każda realizacja daje widmo o innej postaci, co utrudnia ocenę rzeczywistej gęstości widmowej mocy sygnału. Aby otrzymać bardziej stabilne i reprezentatywne oszacowanie PSD, stosuje się techniki uśredniania, z których najpopularniejszą jest metoda Welcha (ang. Welch’s Method). Polega ona na podziale sygnału na zachodzące na siebie segmenty, okienkowaniu każdego z nich oraz uśrednieniu uzyskanych periodogramów cząstkowych. Takie podejście znacząco zmniejsza wariancję estymatora PSD kosztem pogorszenia rozdzielczości częstotliwościowej, co w praktyce stanowi korzystny kompromis.