Podręcznik

Procesy losowe są fundamentem teorii sygnałów w przypadkach, gdy analizowane sygnały wykazują charakter stochastyczny. W przetwarzaniu sygnałów szczególnie istotne jest statystyczne opisanie ich właściwości, ponieważ pojedyncza realizacja sygnału może nie dawać pełnego obrazu jego zachowania. Do podstawowych właściwości statystycznych procesu losowego należą wartość oczekiwana oraz wariancja.

Dla ciągłego procesu losowego \( X(t) \) wartość oczekiwana w czasie \( t \) to średnia po wszystkich możliwych realizacjach procesu w tym momencie czasu:

gdzie funkcja gęstości prawdopodobieństwa \( f_{X(t)}(x) \) zależy od wartości zmiennej losowej \( x \) w danym czasie \( t \). W praktyce wartość oczekiwana pozwala określić typowy poziom sygnału w danym punkcie czasowym.

Wariancja opisuje rozrzut wartości sygnału wokół średniej w danym momencie czasu:

Wariancja pozwala określić, jak bardzo realizacje procesu różnią się od wartości oczekiwanej. Wariancja jest istotna przy analizie zmian amplitudy sygnału oraz przy wyznaczaniu pasma dynamiki szumu w systemach przetwarzania sygnałów. W praktyce wygodniej jest korzystać z pojęcia odchylenia standardowego:

Z pojęciem wartości oczekiwanej związana jest funkcja autokorelacji:

gdzie dwuwymiarowa funkcja gęstości prawdopodobieństwa \( f_{X(t_1),X(t_2)}(x_1,x_2) \) zależy od wartości zmiennych losowych \( x_1 \) i \( x_2 \) w czasie, odpowiednio \( t_1 \) i \( t_2 \).

Analogicznie można zdefiniować funkcję kowariancji:

Obydwie charakterystyki opisują liniową zależność między wartościami procesu losowego \( X(t) \) w dwóch różnych momentach czasu. Autokorelacja uwzględnia średnią sygnału, natomiast kowariancja mierzy zależności próbek po usunięciu wpływu wartości średniej, pokazując jedynie zmienną część procesu. Do podstawowych własności funkcji kowariancji należą:

• \( C_{XX}(t_1,t_2)=C_{XX}(t_2,t_1) \) – symetria,
• \( C_{XX}(t,t)=\sigma^2_X(t) \) – kowariancja w tym samym punkcie czasowym to wariancja.

Zauważmy, że kowariancja podaje siłę zależności, ale jej wartość zależy od jednostek i wariancji sygnału. Dokonując normalizacji funkcji kowariancji, otrzymamy unormowaną kowariancję, czyli współczynnik korelacji:

którego wartości mieszczą się w przedziale \( [-1,1] \). Wtedy otrzymujemy relatywną siłę korelacji, niezależnie od jednostek lub amplitudy sygnału.

Analiza zmienności powyższych parametrów sygnałów w czasie prowadzi do rozróżnienia procesów stacjonarnych i niestacjonarnych. Proces stacjonarny w szerokim sensie (WSS, ang. Wide-Sense Stationary) to taki proces losowy, którego średnia i wariancja nie zależą od czasu:

co ułatwia modelowanie i analizę w dziedzinie częstotliwości.

Proces niestacjonarny charakteryzuje się tym, że \( \mu_X(t) \) i/lub wariancja \( \sigma^2_X(t) \) zmieniają się w czasie. W praktyce oznacza to, że właściwości sygnału obserwowane w jednym przedziale czasowym niekoniecznie opisują zachowanie sygnału w innym przedziale. Przykładem może być sygnał EEG, którego amplituda i średnia zmieniają się w zależności od stanu pacjenta.

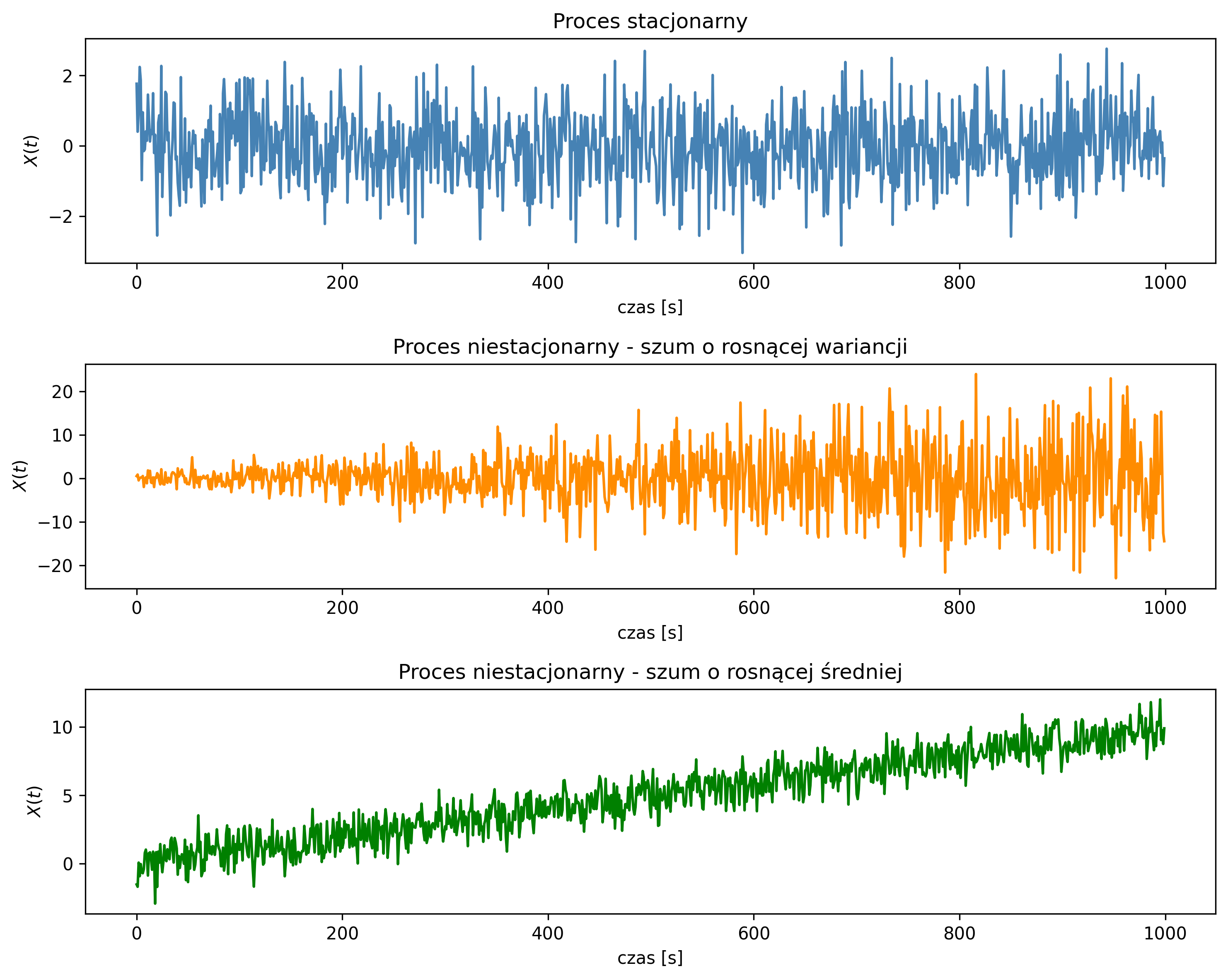
Na rys. 5.2 pokazano przykładowy przebieg procesu stacjonarnego i niestacjonarnego – ze względu na średnią i wariancję. Pierwszy wykres wskazuje na proces o stałej średniej i wariancji. Na drugim wykresie, proces niestacjonarny ma coraz większe odchylenia od zera, gdyż jego wariancja rośnie. Ostatni wykres ilustruje proces niestacjonarny ze względu na liniowo rosnącą średnią.

Dla procesu stacjonarnego funkcja autokorelacji i kowariancji oraz współczynnik korelacji zależą tylko od różnicy czasu \( \tau=t_2-t_1 \):

gdzie \( C_{XX}(0)=\sigma^2_X \) jest wariancją sygnału. Zauważmy, że jeśli \( \mu=0 \), to \( R_{XX}(\tau)=C_{XX}(\tau) \). W przypadku \( \tau=0 \):

Funkcja korelacji zawiera w sobie informację o wariancji i średniej realizacji procesu losowego. Z wykresu funkcji korelacji możemy odczytać, jak długo sygnał pamięta swoje przeszłe wartości, czy zależność jest dodatnia czy ujemna, czy proces ma składowe okresowe, a także łatwo porównywać różne sygnały, niezależnie od ich skali:

• siła zależności między próbkami sygnału:
  • \( |R_{XX}(\tau)|\approx 1 \) – wartości w momentach \( t \) i \( t+\tau \) są silnie powiązane,
  • \( |R_{XX}(\tau)|\approx 0 \) – brak związku,
• kierunek zależności:
  • \( R_{XX}(\tau)>0 \) – dodatnia korelacja,
  • \( R_{XX}(\tau)<0 \) – ujemna korelacja,
• okresowość:
  • jeśli funkcja \( R_{XX}(\tau) \) jest okresowa, to proces ma składowe harmoniczne,
• czas korelacji (czas pamięci procesu):
  • im szybciej funkcja \( R_{XX}(\tau) \) opada do zera, tym proces ma krótszą „pamięć” (próbki szybko stają się niezależne).

Przykładem procesu losowego, w którym kolejne próbki są niezależne od pozostałych i mają zerową korelację, jest biały szum. W przetwarzaniu sygnałów biały szum jest często używany jako model zakłóceń losowych lub model sygnału testowego dla systemów liniowych. Do jego charakterystycznych cech należy brak pamięci – autokorelacja jest prawie zerowa dla wszystkich opóźnień poza zerowym, stąd wartość sygnału w dowolnym czasie nie zależy od wartości przeszłych. Biały szum gaussowski to szczególny przypadek białego szumu, którego próbki mają rozkład normalny (Gaussa). Jest szeroko stosowany w analizie sygnałów i systemów liniowych, zwłaszcza w modelowaniu zakłóceń i w teorii filtrów optymalnych. Zarówno biały szum, jak i biały szum gaussowski są procesami losowymi stacjonarnymi w szerokim sensie, czyli mają stałą wartość oczekiwaną (zwykle przyjmuje się \(0\)) i wariancję.

Na rys. 5.3 pokazano, jak funkcja korelacji ujawnia pamięć sygnału i okresowość. Wykresy sygnału sinusoidalnego, sygnału sinusoidalnego z dodanym białym szumem i samego białego szumu oraz odpowiadające im funkcje korelacji uwidaczniają charakterystyczne cechy ich przebiegów. Rozkład korelacji w czasie pokazuje, jak długo sygnały „pamiętają” swoje wartości. Normalizacja pozwala porównywać sygnały niezależnie od amplitudy.

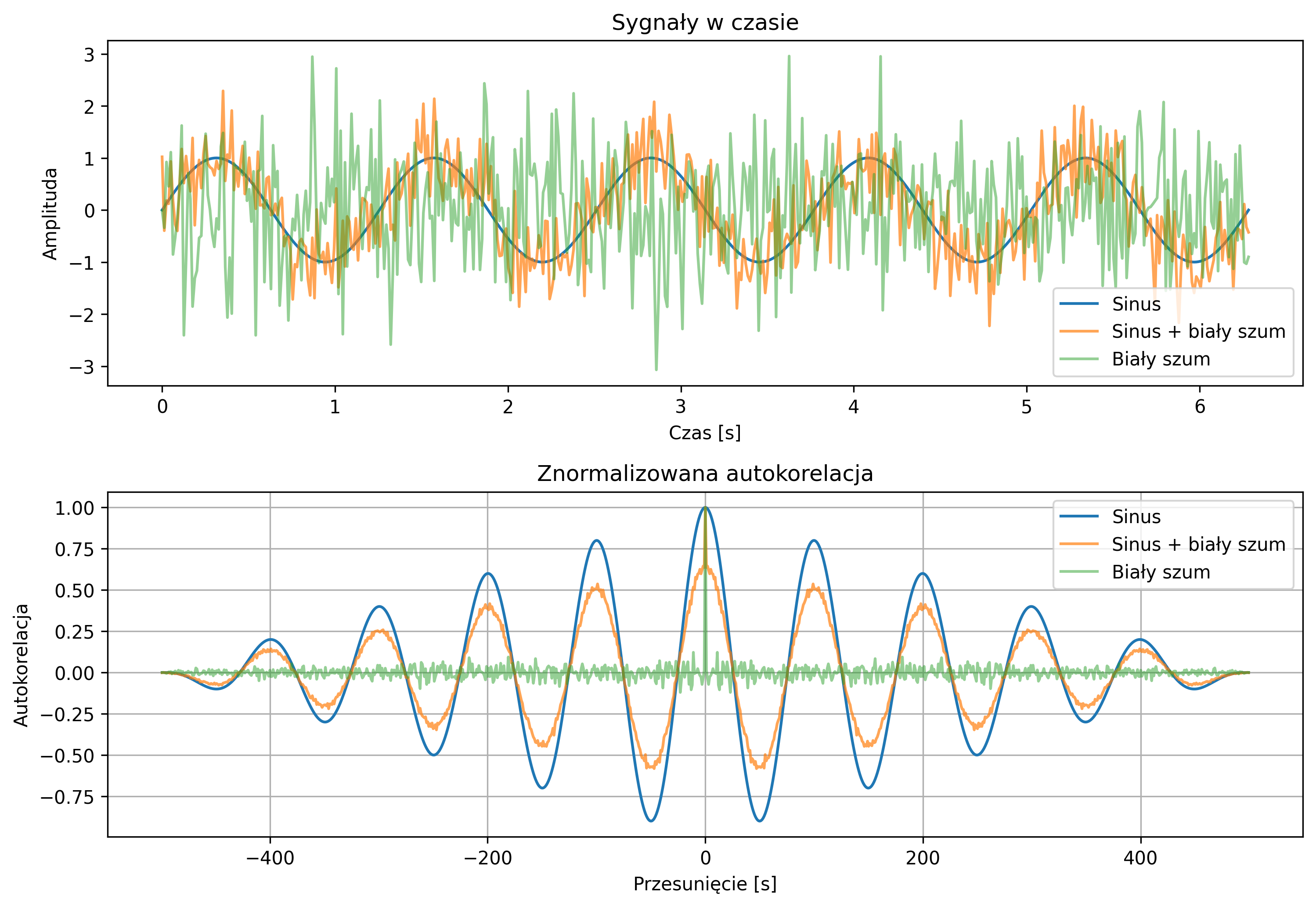
Sygnał sinusoidalny ma wyraźną periodyczną funkcję korelacji – na wykresie pojawiają się maksima i minima lokalne w regularnych odstępach. Oznacza to, że wartości sygnału w określonych przesunięciach są ze sobą silnie powiązane (dodatnio lub ujemnie). Innymi słowy, sygnał „pamięta” swoje przeszłe wartości i ma charakter okresowy. Biały szum ma funkcję korelacji bliską zeru dla wszystkich opóźnień poza zerowym. Wartości próbek są praktycznie niezależne od siebie, a proces nie ma pamięci. Korelacja pokazuje tylko pojedynczy impuls w \( \tau=0 \), czyli sygnał nie zawiera periodyczności. Sygnał sinusoidalny z dodanym białym szumem ma funkcję korelacji, w której nadal widoczne są periodyczne maksima i minima lokalne, jednak są one mniejsze i mniej regularne niż w przypadku czystego sinusa. Oznacza to, że sygnał wciąż zachowuje pewną pamięć swojej struktury okresowej, ale szum częściowo ją „maskuje”, wprowadzając przypadkowe zakłócenia i obniżając poziom korelacji.

Poza stacjonarnością istotnym pojęciem w teorii procesów losowych jest także ergodyczność. Proces losowy jest stacjonarny, gdy jego parametry statystyczne nie zmieniają się w czasie. Jednak w praktyce często dysponujemy tylko jedną długą realizacją procesu i chcielibyśmy z niej oszacować te parametry. Proces losowy \( X(t) \) nazywamy ergodycznym w sensie wartości średniej, jeśli średnia czasowa z jednej realizacji jest równa wartości oczekiwanej:

Proces losowy \( X(t) \) nazywamy ergodycznym w sensie drugiego rzędu, jeżeli jego wartości średnie i korelacje można wyznaczyć na podstawie jednej realizacji w czasie. Oznacza to, że spełnione są zależności:

Oznacza to, że właściwości statystyczne procesu (np. wartość oczekiwana, wariancja, funkcja autokorelacji) można wyznaczyć nie tylko jako średnie po wielu realizacjach procesu (uśrednianie w przestrzeni prawdopodobieństwa), ale także jako średnie wzdłuż jednej, odpowiednio długiej realizacji (uśrednianie w czasie).

W praktyce proces stacjonarny nie zawsze jest ergodyczny. Dla procesów stacjonarnych, które nie spełniają warunku ergodyczności, pojedyncza realizacja procesu nie wystarczy do pełnego odtworzenia charakterystyk – konieczne byłoby dysponowanie wieloma realizacjami. Natomiast w przypadku procesów ergodycznych (np. białego szumu gaussowskiego), analiza jednego długiego przebiegu procesu daje dostęp do wszystkich potrzebnych informacji statystycznych.

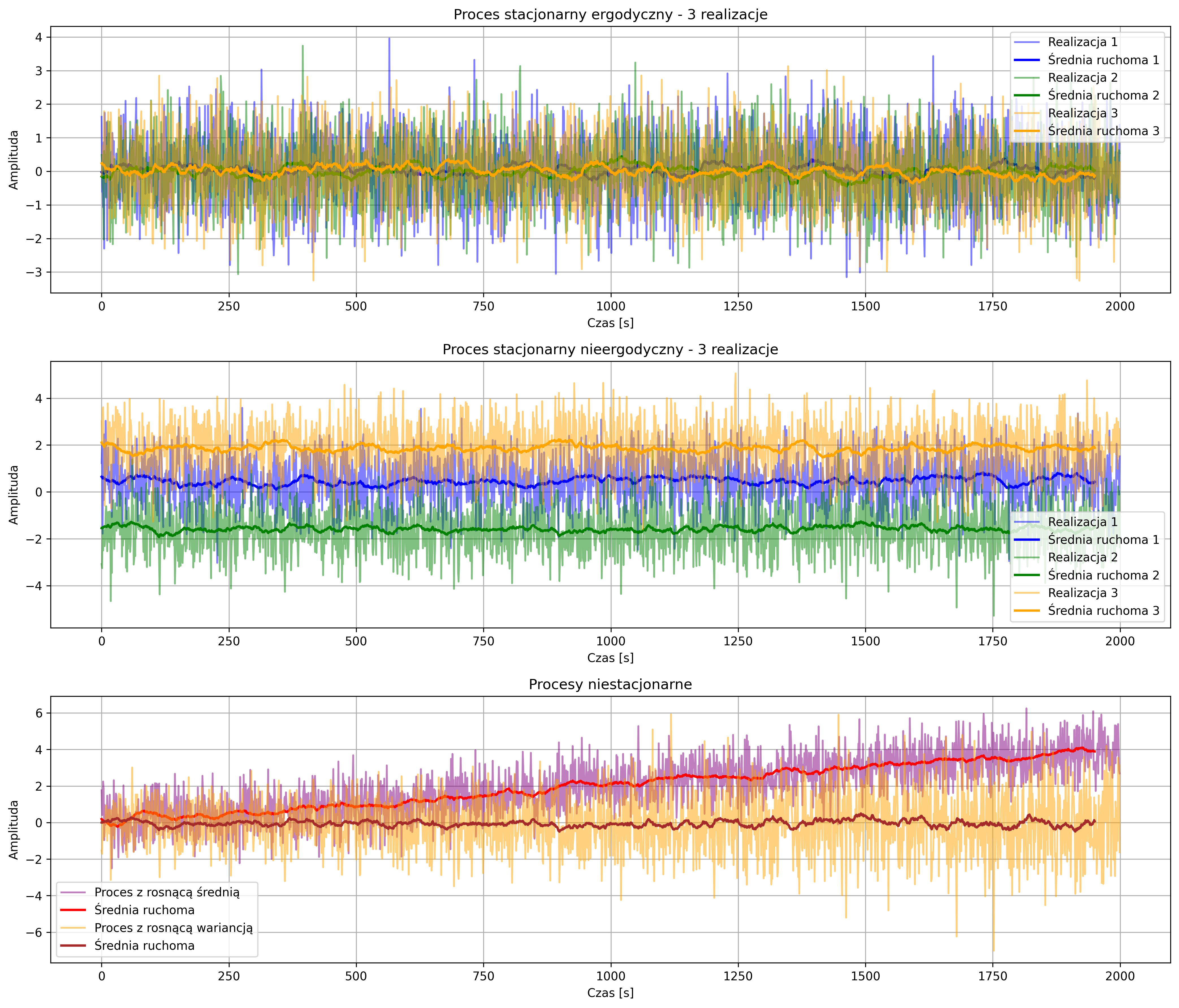
Na pierwszym wykresie rys. 5.4 pokazano trzy niezależne realizacje procesu o stałej średniej i wariancji. Średnie ruchome – wygładzenie sygnału w celu obserwacji lokalnych zmian średniej w czasie (grubsze linie w tych samych kolorach co realizacje) – oscylują wokół tej samej wartości, pokazując, że statystyki jednej realizacji dobrze odzwierciedlają statystyki całego procesu. W przypadku drugiego wykresu, średnie ruchome realizacji pokazują różne poziomy – widać, że statystyki jednej realizacji nie odzwierciedlają statystyk całego procesu, czyli proces nie jest ergodyczny, ale ze względu na stałą wariancję i średnią (każda realizacja procesu z inną, ale stałą średnią) proces jest stacjonarny. Ostatni wykres ilustruje procesy niestacjonarne – ze względu na rosnącą średnią i ze względu na rosnącą wariancję. Średnia ruchoma dla jednego procesu pokazuje wyraźny trend, zaś w przypadku drugiego procesu – pomimo stałości średniej – obserwujemy wzrost zmienności sygnału, co obrazuje brak stacjonarności.

Własność stacjonarności i ergodyczności można również odczytać z wykresu funkcji autokorelacji. W przypadku procesu stacjonarnego funkcja autokorelacji zależy tylko od przesunięcia, a nie od czasu \( t \). Jeśli proces jest stacjonarny i ergodyczny, wszystkie realizacje procesu mają podobną wartość \( R_{XX}(0) \) – średnia i wariancja nie zmieniają się w czasie. Jeśli proces nie jest ergodyczny, realizacje procesu mają różne poziomy przy przesunięciu \( \tau=0 \). Jeśli realizacje mają zarówno różne poziomy, jak i kształty, będziemy mieli do czynienia z procesem niestacjonarnym.

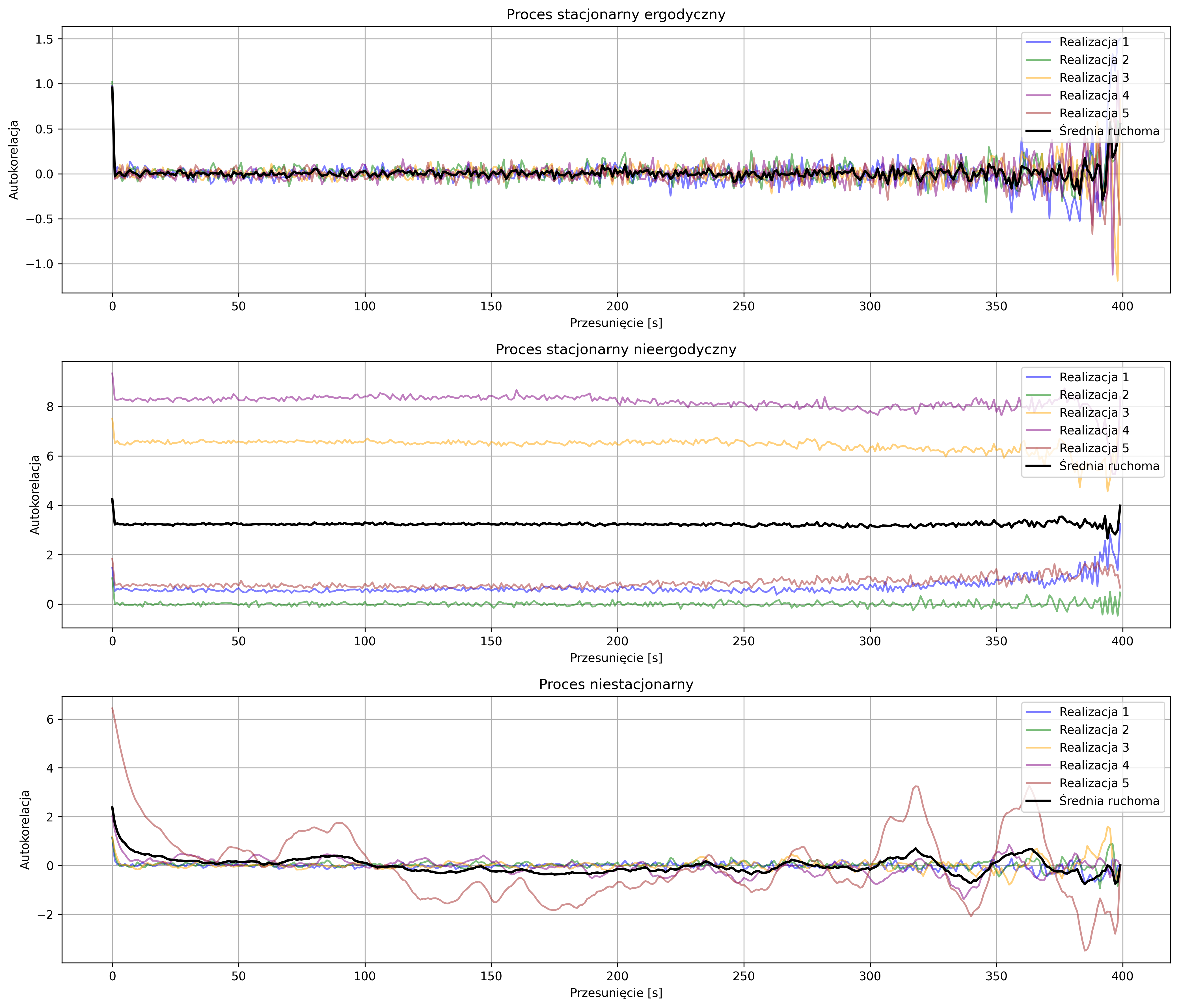
Funkcja autokorelacji stacjonarnego procesu ergodycznego została zilustrowana na górnym wykresie rys. 5.5. Wszystkie realizacje procesu mają podobną wartość \( R_{XX}(0) \) – średnia i wariancja nie zmieniają się w czasie, autokorelacje różnych realizacji procesu nakładają się, a średnia autokorelacja (czarna grubsza linia) dobrze opisuje każdą realizację. W przypadku drugiego wykresu mamy do czynienia z realizacjami, z których każda funkcja autokorelacji ma inną (stałą) średnią – autokorelacje różnych realizacji mają różne poziomy, a średnia autokorelacja nie pokrywa się z żadną realizacją – widać brak ergodyczności. Proces niestacjonarny przedstawiony na ostatnim wykresie charakteryzuje się wyraźnie różnymi kształtami – statystyki zmieniają się w czasie, a średnia autokorelacja nie oddaje właściwości żadnej realizacji.