Podręcznik
1. Równania stanu dla obiektów nieliniowych
1.1. Przykład modelowania układu trzech zbiorników
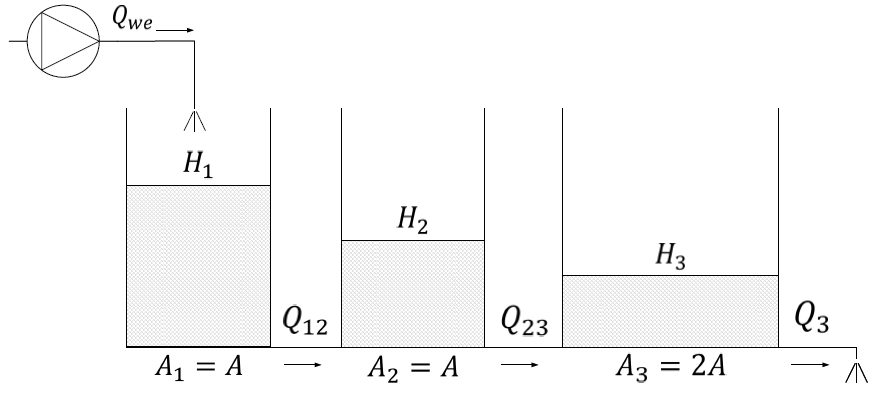
Rysunek 1.1 Schemat układu trzech zbiorników.
Naszym nadrzędnym celem jest regulacja poziomów cieczy w zbiornikach, które oznaczamy jako \( H_1(t) \), \( H_2(t) \) oraz \( H_3(t) \). Z tego względu zależy nam na sformułowaniu opisu zmian w czasie poziomów cieczy w zbiornikach. Jak się okaże w trakcie dalszych rozważań, dla obiektu z jednym sygnałem sterującym (w naszym przypadku \( Q_{we} \)) niemożliwa jest niezależna regulacja poziomów wody w każdym trzech zbiorników. Możemy swobodnie regulować poziom cieczy w jednym ze zbiorników, natomiast poziomy cieczy w pozostałych zbiornikach będą wynikały z własności układu. Ten poziom, który chcemy swobodnie zmieniać pełni rolę sygnału wyjściowego. Przyjmujemy, że sygnałem wyjściowym w naszym układzie jest poziom cieczy w trzecim zbiorniku \( H_3(t) \).
W niniejszym kursie skupiamy się na obiektach, które można opisać za pomocą układu równań różniczkowych zwyczajnych i właśnie taki opis sformułujemy dla układu trzech zbiorników. Proces tworzenia modelu obiektu zaczynamy od sformułowania równań fizycznych opisujących różne procesy zachodzące w obiekcie, a następnie przekształcamy te równania do dogodniejszej postaci. W przypadku układu trzech zbiorników trzon modelu stanowią równania bilansu objętości cieczy w każdym zbiorniku. Zakładamy, że ciecz jest nieściśliwa, dlatego równania bilansu objętości są równoważne z zasadą zachowania masy. Równania bilansu objętości formułujemy w postaci różniczkowej wg ogólnego schematu:
szybkość zmian objętości cieczy = natężenie dopływu cieczy - natężenie odpływu cieczy
Odpowiednie równania różniczkowe dla trzech zbiorników mają postać
\( \begin{matrix}
\dfrac{dV_1(t)}{dt} &=& Q_{we}(t) - Q_{12}(t) \qquad(1.1)\\
\dfrac{dV_2(t)}{dt} &=& Q_{12}(t) - Q_{23}(t) \qquad(1.2)\\
\dfrac{dV_3(t)}{dt} &=& Q_{23}(t) - Q_{3}(t) \qquad(1.3)
\end{matrix} \)
gdzie objętości cieczy $ V_1(t) $, $ V_2(t) $ oraz $ V_3(t) $ w zbiornikach wynoszą
\( \begin{matrix}
V_1(t) &=& A_1 H_1(t) = A\cdot H_1(t) \qquad(1.4)\\
V_2(t) &=& A_2 H_2(t) = A\cdot H_2(t) \qquad(1.5)\\
V_3(t) &=& A_3 H_3(t) = 2A\cdot H_3(t) \qquad(1.6)
\end{matrix} \)
Kolejne równania określają przepływ cieczy pomiędzy zbiornikami. Przepływ cieczy /( Q /) przez przewód lub zawór jest zwykle modelowany za pomocą równania
\( \begin{equation} Q=k\sqrt{\Delta p} \qquad(1.7) \end{equation} \)
gdzie \( \Delta p = p_a-p_b \) oznacza różnicę ciśnień na końcach \( a \) i \( b \) przewodu (lub zaworu), natomiast \( k \) jest stałą zależną od właściwości cieczy i geometrii przewodu. Przepływy \( Q_{12} \), \( Q_{23} \) oraz \( Q_{3} \) są wymuszane przez ciśnienia hydrostatyczne generowane przez słupy cieczy. Ciśnienie hydrostatyczne \( p \) jest dane wzorem
\( \begin{equation}
p = p_{atm}+\rho g H
\qquad(1.8)
\end{equation} \)
gdzie \( p_{atm} \) - ciśnienie atmosferyczne, \( \rho \) - gęstość cieczy, \( g \) - przyśpieszenie ziemskie, \( H \) wysokość słupa cieczy. Jeżeli wstawimy zależność (1.8) do równania (\1.7) to otrzymamy
\( \begin{eqnarray} Q&=&k\sqrt{\Delta p} = k\sqrt{p_a-p_b} = k\sqrt{p_{atm}+\rho g H_a-p_{atm}-\rho g H_b} \qquad(1.9)\\ &=& k\sqrt{\rho g H_a-\rho g H_b} = k\sqrt{\rho g \Delta H} = k\sqrt{\rho g} \sqrt{ \Delta H} = \alpha \sqrt{ \Delta H} \qquad(1.10) \end{eqnarray} \)
gdzie \( \alpha = k\sqrt{\rho g} \) jest stałą, a \( \Delta H = H_a-H_b \) to różnica wysokości słupów cieczy na końcach \( a \) i \( b \) przewodu. Dla uproszczenia opisu zakładamy, że wszystkie przewody przepływowe (lub zawory) są identyczne i współczynnik \( \alpha \) jest taki sam dla przepływów \( Q_{12} \), \( Q_{23} \) oraz \( Q_{3} \). Przepływy między zbiornikami są zatem dane wzorami
\( \begin{eqnarray} Q_{12}(t) &=& \alpha \sqrt{H_1(t)-H_2(t)} \qquad(1.11)\\ Q_{23}(t) &=& \alpha \sqrt{H_2(t)-H_3(t)} \qquad(1.12)\\ Q_{3}(t) &=& \alpha \sqrt{H_3(t)-0} = \alpha \sqrt{H_3(t)} \qquad(1.13) \end{eqnarray} \)
Powyższe wzory są prawidłowe pod warunkiem, że wyrażenia pod pierwiastkami są nieujemne. W przypadku, gdy znak wyrażenia pod pierwiastkiem mógłby się zmieniać należałoby zastosować wzór
\( \begin{equation} Q = sgn (\Delta H) \alpha \sqrt{| \Delta H|} \qquad(1.14) \end{equation} \)
gdzie operator \( sgn(\cdot) \) zwraca znak wyrażenia. Wykorzystanie wyrażenia \( sgn(\cdot) \) wprowadza jednak nieciągłość do opisu obiektu. Dla naszych potrzeb zakładamy, że wyrażenia pod pierwiastkami we wzorach (1.11)-(1.13) są zawsze nieujemne. Jest to uzasadnione założenie, gdyż w układach regulacji rozważamy zachowanie układu w pobliżu punktu pracy, gdzie, jak zobaczymy w kolejnej sekcji, te warunki istotnie są spełnione.
Równania (1.1) - (1.6) oraz (1.11)-(1.13) dają nam pełny opis zjawisk fizycznych zachodzących w układzie trzech zbiorników. Zauważmy, że nie uwzględniliśmy w opisie obiektu wszystkich zjawisk np.: możliwego przelania się cieczy w zbiornikach, nieszczelności prowadzących do wycieków lub przytykania się zaworów. Stopień szczegółowości opisu obiektu jest uzależniony od tego, do jakich celów jest wykorzystywany model. Jeżeli model miałby być wykorzystywany do celów diagnostyki opis ww. zjawisk byłby niezbędny. Naszym celem jest jednak przestudiowanie procesu syntezy układu regulacji i do tego celu zaprezentowany sposób opisu układu jest wystarczający.
Kolejnym krokiem przy formułowaniu modelu obiektu nieliniowego jest przekształcenie równań fizycznych do równoważnej, ale dogodniejszej postaci. W przypadku układów regulacji, jak i całej teorii sterowania równania różniczkowe są przedstawiane standardowo w postaci tzw. równań stanu. Teraz dokonamy przekształcenia równań fizycznych układu trzech zbiorników do postaci równań stanu, by następnie omówić cechy charakterystyczne tej postaci.
Wstawiając zależności (1.11)-(1.13) do równań (1.1)-(1.3) otrzymujemy
\( \begin{eqnarray} \frac{dV_1(t)}{dt} &=& Q_{we}(t) - \alpha \sqrt{H_1(t)-H_2(t)} \qquad(1.15) \\ \frac{dV_2(t)}{dt} &=& \alpha \sqrt{H_1(t)-H_2(t)} - \alpha \sqrt{H_2(t)-H_3(t)} \qquad(1.16)\\ \frac{dV_3(t)}{dt} &=& \alpha\sqrt{H_2(t)-H_3(t)} - \alpha \sqrt{H_3(t)} \qquad(1.17) \end{eqnarray} \)
Ponieważ pole podstawy zbiornika jest stałe, pochodna objętości cieczy w każdym zbiorniku spełnia warunek
\( \begin{equation} \dfrac{dV(t)}{dt} = \dfrac{d(A\cdot H(t))}{dt} = A \cdot \dfrac{dH(t)}{dt} \qquad(1.18) \end{equation} \)
Wstawiając (1.18) do wzorów (1.15)-(1.17) otrzymujemy
\( \begin{eqnarray} A\frac{d H_1(t)}{dt}&=& Q_{we}(t) - \alpha \sqrt{H_1(t)-H_2(t)} \qquad(1.19) \\ A\frac{d H_2(t)}{dt} &=& \alpha \sqrt{H_1(t)-H_2(t)} - \alpha \sqrt{H_2(t)-H_3(t)} \qquad(1.20)\\ 2A\frac{d H_3(t)}{dt} &=& \alpha\sqrt{H_2(t)-H_3(t)} - \alpha \sqrt{H_3(t)} \qquad(1.21) \end{eqnarray} \)
Podzielmy jeszcze obie strony każdego równań (1.19)-(\1.21) przez wartość odpowiedniego pola powierzchni podstawy zbiornika, aby otrzymać równania stanu dla układu trzech zbiorników
\( \begin{eqnarray} \frac{d H_1(t)}{dt} &=& \frac{1}{A}Q_{we}(t) - \frac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(1.22) \\ \frac{d H_2(t)}{dt} &=& \frac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \frac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(1.23) \\ \frac{d H_3(t)}{dt} &=& \frac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \frac{\alpha}{2A} \sqrt{H_3(t)} \qquad(1.24) \end{eqnarray} \)
Powyższe równania są równoważne równaniom fizycznym układu, jednak jest kilka cech wyróżniających równania stanu od innych równoważnych postaci. Po lewej stronie każdego z równań stanu znajduje się jedynie pochodna wysokości słupa cieczy w odpowiednim zbiorniku. Zmienne, których pochodne znajdują się po lewych stronach równań stanu nazywane są zmiennymi stanu. Dla układu trzech zbiorników zmiennymi stanu są \( H_1 \), \( H_2 \) oraz \( H_3 \). Po prawej stronie każdego z równań stanu znajduje się (być może skomplikowana i nieliniowa) funkcja. Argumentami tej funkcji mogą być jedynie trzy kategorie zmiennych
- zmienne stanu
- sygnały sterujące
- stałe
W rozważanym przykładzie zmiennymi stanu są \( H_1 \), \( H_2 \) oraz \( H_3 \), sygnałem sterującym jest \( Q_{we} \), natomiast stałymi są \( A \) oraz \( \alpha \). Z równań stanu zostały wyeliminowane inne zmienne (przepływy i objętości), pośrednio związane ww. zmiennymi.
Aby rozwiązać równania stanu czy to analitycznie, czy numerycznie, konieczne jest określenie warunków początkowych dla zmiennych stanu tzn. wielkości \( H_1(t_0) \), \( H_2(t_0) \) oraz \( H_3(t_0) \), gdzie \( t_0 \) jest wybraną chwilą początkową. Konieczna jest też znajomość wartości sygnału sterującego \( Q_{we}(t) \) na całym rozważanym horyzoncie czasu.
Równania stanu układu trzech zbiorników można rozwiązać numerycznie w środowisku MATLAB®. Na potrzeby symulacji przyjmujemy następujące wartości parametrów obiektu \( A = 0.5 \) , \( \alpha = 1 \). Na Rys. 1.2 przedstawiono przykładowe trajektorie stanów obiektu uzyskane dla stałego przepływu cieczy przez pompę \( Q_{we}(t) =0.5\) i zerowych warunków początkowych
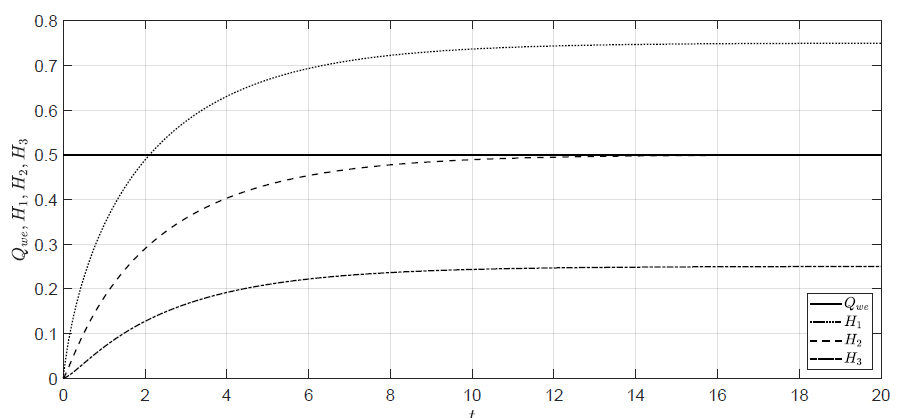
Rysunek 1.2 Trajektorie poziomów cieczy w zbiornikach dla stałego sterowania i zerowych warunków początkowych.
Przedstawione przebiegi ilustrują proces napełniania zbiorników cieczą. Początkowo puste zbiorniki napełniają się do pewnych poziomów aż do momentu, w którym w obiekcie ustali się równowaga przepływów. Po ustaleniu się równowagi przepływów, nie następują już dalsze zmiany poziomów cieczy.
Na Rys. 1.3 przedstawiono trajektorie sterowania i stanów obiektu uzyskane dla stałego przepływu cieczy przez pompę \( Q_{we}(t) =0.5\) i niezerowych warunków początkowych \( H_1(t_0) =0.8 \), \( H_2(t_0) =0.4 \), \( H_3(t_0)=0.3 \).
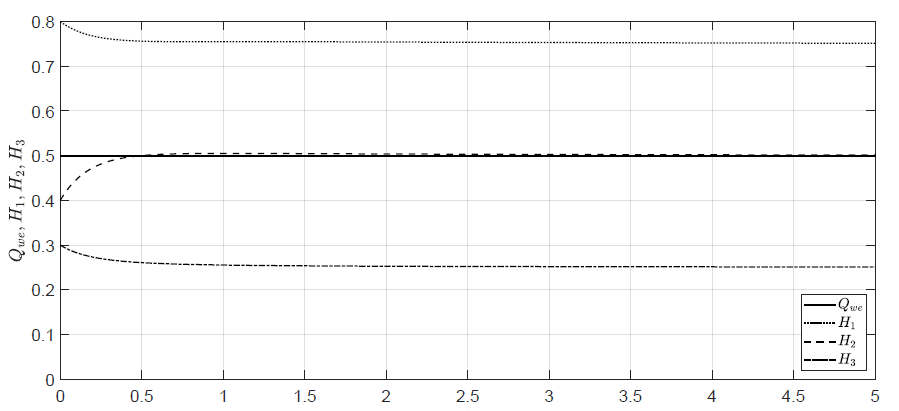
Rysunek 1.3 Trajektorie poziomów cieczy w zbiornikach dla stałego sterowania i niezerowych warunków początkowych.
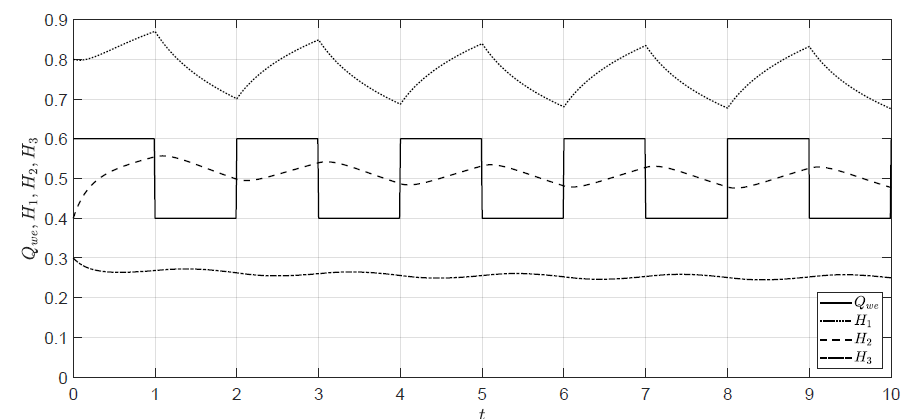
Rysunek 1.4 Trajektorie zmiennych poziomów cieczy w zbiornikach dla niezerowych warunków początkowych i sterowania w kształcie fali prostokątnej.
Poziomy cieczy w zbiornikach zmieniają się aż do chwili w której powstanie w obiekcie równowaga przepływów. Po ustaleniu się równowagi przepływów, nie następują już dalsze zmiany poziomów cieczy. Zauważmy, że poziomy cieczy ustaliły się na takich samych wartościach jak w przypadku napełniania pustych zbiorników. Ponieważ tym razem zbiorniki są w chwili początkowej napełnione do pewnych niezerowych poziomów, to czas ustalenia się równowagi przepływów jest krótszy niż w przypadku napełniania pustych zbiorników.
Na Rys. 1.4 przedstawione zostały trajektorie sterowań i stanów obiektu dla niezerowych warunków początkowych \( H_1(t_0) =0.8 \), \( H_2(t_0) =0.4 \), \( H_3(t_0)=0.3 \) i sygnału sterującego typu fala prostokątna.
Amplituda wahań \( Q_{we}(t) \) wokół wartości 0.5 wynosi 0.1. Wypełnienie fali wynosi 50\%, natomiast jej okres wynosi 2. Poziomy cieczy we wszystkich zbiornikach doznają wahań. Dla kolejnych zbiorników następuje stopniowe wygładzanie przebiegów i spadek amplitudy wahań. Symulacja numeryczna pozwala analizować zachowanie obiektu także dla innych przebiegów sygnału sterującego \( Q_{we}(t) \).
