Podręcznik

W niniejszej sekcji sformułujemy model odwróconego wahadła matematycznego w postaci równań stanu. Schemat wahadła został przedstawiony na Rys. 1.5.

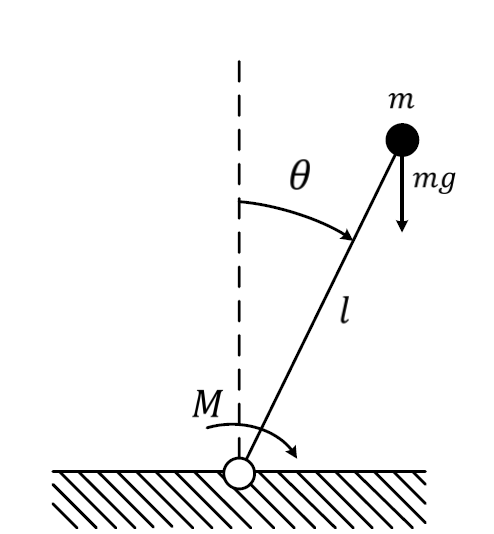
Rysunek 1.5 Schemat wahadła matematycznego.

Masa $m$ jest osadzona na sztywnym przegubowym pręcie o długości $l$ (pomijamy masę pręta). W przegubie podawany jest sterowany moment siły $M$, a na masę $m$ działa siła przyciągania ziemskiego ($g$ - przyciąganie ziemskie). W przegubie generuje się też moment tarcia proporcjonalny do prędkości kątowej wahadła. Kąt odchylenie pręta od osi pionowej jest oznaczony jako $\theta$. Równanie fizyczne opisujące układ to równanie Newtona dla ruchu obrotowego. Ogólna postać tego równania to

$\begin{equation} I\epsilon(t) = \sum_{i} M_i(t) \qquad(1.25) \end{equation}$

tzn. iloczyn momentu bezwładności ciała $I$ i przyśpieszenia kątowego $\epsilon$ jest równy sumie momentów sił $M_i$ działających na ciało. Moment bezładności wahadła obliczamy przy upraszczającym założeniu o punktowości masy $m$ i pomijalnej masie pręta. W takim przypadku mamy

$\begin{equation} I = ml^2 \qquad(1.26) \end{equation}$

przyśpieszenie kątowe jest równe drugiej pochodnej położenia kątowego

$\begin{equation} \epsilon(t) = \dfrac{d^2\theta(t)}{dt^2} \qquad(1.27) \end{equation}$

Na ciało działa moment bezwładności w przegubie $M$, moment tarcia $M_t$ oraz moment siły generowany przez siłę przyciągania ziemskiego $M_g$

$\begin{equation} \sum_{i} M_i(t) = M(t) + M_t(t) + M_g(t) \qquad(1.28) \end{equation}$

Moment tarcia jest proporcjonalny do prędkości kątowej $\omega$, ze współczynnikiem proporcjonalności $D$

$\begin{equation} M_t(t) = -D\omega(t) = -D\dfrac{d\theta(t)}{dt} \qquad(1.29) \end{equation}$

Znak minus wskazuje na to, że moment tarcia działa przeciwnie do aktualnej prędkości kątowej. Moment siły od grawitacji jest równy iloczynowi siły ciążenia $F_g=mg$, długości ramienia $l$ na którym działa siła grawitacji oraz sinusowi kąta pomiędzy ramieniem a wektorem siły 

$\begin{equation} M_g(t) = F_g\cdot l \cdot sin\theta(t) = mglsin\theta(t) \qquad(1.30) \end{equation}$

Wstawiając zależności (1.26)-(1.30) do równania (1.25) otrzymujemy

$\begin{equation} ml^2 \dfrac{d^2\theta(t)}{dt^2} = mglsin\theta(t) - D \dfrac{d\theta(t)}{dt} + M(t) \qquad(1.31) \end{equation}$

  Po podzieleniu obu stron równania przez $ml^2$ otrzymujemy

$\begin{equation} \dfrac{d^2\theta(t)}{dt^2} = \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \dfrac{d\theta(t)}{dt} +\dfrac{1}{ml^2} M(t) \qquad(1.32) \end{equation}$

Równanie różniczkowe (1.32) jest równaniem drugiego rzędu. Równania stanu są równaniami pierwszego rzędu. Możemy przekształcić równanie (1.32) do dwóch równań pierwszego rzędu poprzez wprowadzenie do równań zmiennej oznaczającej prędkość kątowej

$\begin{equation} \omega = \dfrac{d\theta(t)}{dt} \qquad(1.33) \end{equation}$

Pierwsza pochodna prędkości kątowej jest równa drugiej pochodnej położenia kątowego 

$\begin{equation} \dfrac{d\omega(t)}{dt} = \dfrac{d^2\theta(t)}{dt^2} \qquad(1.34) \end{equation}$

Wprowadzając powyższe zależności do (1.32) otrzymujemy równania stanu wahadła

$\begin{eqnarray} \dfrac{d\theta(t)}{dt} &=& \omega(t) \qquad(1.35)\\ \dfrac{d\omega(t)}{dt} &=& \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} M(t) \qquad(1.36) \end{eqnarray}$

W opisie wahadła zmiennymi stanu są $\theta$ oraz $\omega$, sygnałem sterującym jest moment siły $M$, natomiast stałymi są $g$, $l$, $m$ oraz $D$. Jako sygnał wyjściowy z układu przyjmujemy położenie kątowe $\theta$. Aby rozwiązać równania stanu, konieczne jest określenie warunków początkowych dla zmiennych stanu tzn. wielkości $\theta(t_0)$oraz $\omega(t_0)$, gdzie $t_0$ jest wybraną chwilą początkową. Konieczna jest też znajomość wartości sygnału sterującego $M(t)$ na całym rozważanym horyzoncie czasu.

Równania stanu dla wahadła można rozwiązać numerycznie w środowisku MATLAB®. Na potrzeby symulacji przyjmujemy następujące wartości parametrów obiektu $m = 0.1$, $l = 1$, $g = 10$, $D = 0.1$. Na Rys. 1.6 przedstawiono przykładowe trajektorie stanów obiektu uzyskane dla stałego momentu $M(t) = -0.5$ i warunków początkowych $\theta(t_0) = \dfrac{\pi}{2}$, $\omega(t_0) = 0$

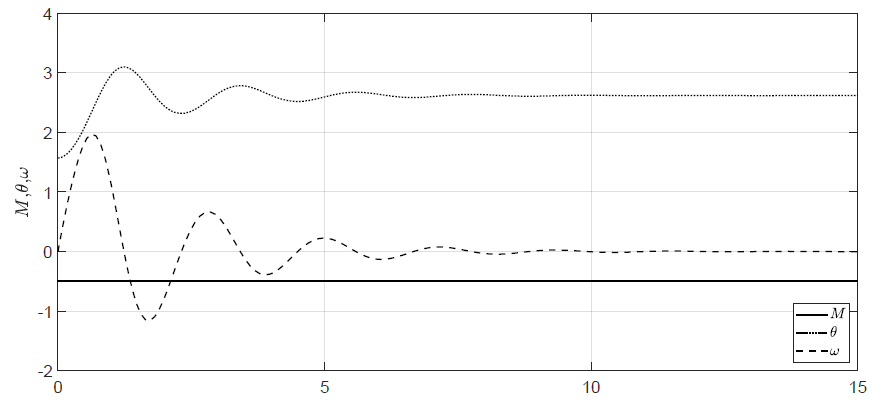
Rysunek 1.6 Trajektorie położenia i prędkości kątowej wahadła dla stałego sterowania.

Wahadło znajdujące się początkowo w położeniu horyzontalnym spada w dół, gdyż moment od siły ciążenia przeważa nad momentem generowanym w przegubie. Następnie, ze względu na obecność tarcia w przegubie, wahadło wykonuje oscylacje gasnące. Wreszcie wahadło stabilizuje się w położeniu, w którym moment od siły ciążenia i $M$ wyrównują się. Po ustabilizowaniu się wahadła w pewnym położeniu kątowym, jego prędkość kątowa wynosi 0. 

Na Rys. 1.7 przedstawione zostały trajektorie stanów obiektu dla  warunków początkowych $\theta(t_0) = \dfrac{\pi}{2}$, $\omega(t_0) = 0$ i sygnału sterującego typu fala prostokątna. Amplituda wahań $M(t)$ wokół wartości -0.5 wynosi 0.1. Wypełnienie fali wynosi 50 %, natomiast jej okres wynosi 2. Po początkowej fazie przejściowej wahadło wykonuje oscylacje o ustalonej amplitudzie.

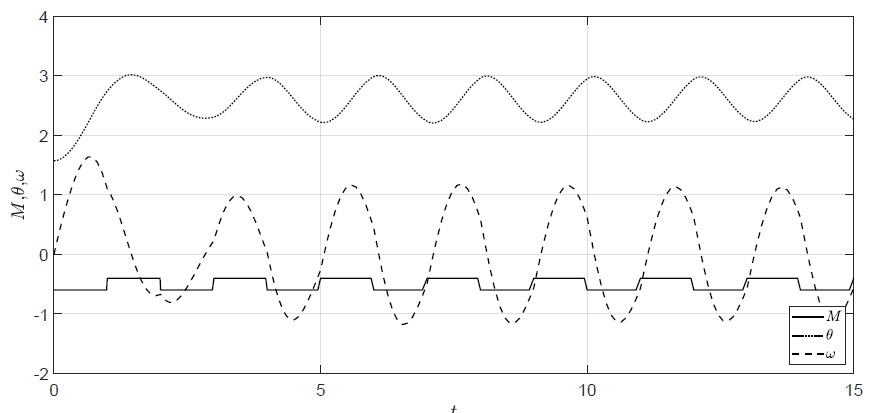
Rysunek 1.7 Trajektorie położenia i prędkości kątowej wahadła dla sterowania w kształcie fali prostokątnej.