Podręcznik

  Aby przetestować zdolność modelu zlinearyzowanego do przybliżania dynamiki obiektu nieliniowego porównajmy przebiegi czasowe zmiennych stanu dla obu modeli. Przyjmujemy parametry obiektu $A = 0.5$, $\alpha = 1$. Wybieramy punkt równowagi $H_{10}=0.75$, $H_{20}=0.5$ $H_{30}=0.25$ oraz $Q_{we0} = 0.5$. Aby porównać zachowanie modelu nieliniowego i zlinearyzowanego rozważamy dwa scenariusze. W pierwszym scenariuszu zakładamy, że w chwili początkowej obiekt nie znajduje się w punkcie równowagi. 

Ponadto przyjmujemy, że sterowanie obiektu jest stałe i równe sterowaniu w punkcie równowagi $Q_{we}(t) = Q_{we0}$. Ze wzoru (1.221) wynika, że sterowanie obiektu zlinearyzowanego wynosi

$\begin{equation} \tilde{Q}_{we}(t) = Q_{we}(t)-Q_{we0} = Q_{we0}-Q_{we0}=0 \end{equation}\qquad(1.244)$

Zmienne stanu obiektu zlinearyzowanego $\tilde{H}_1(t)$, $\tilde{H}_2(t)$ oraz $\tilde{H}_3(t)$ przybliżają przyrosty zmiennych stanu obiektu nieliniowego $\Delta H_1(t)$, $\Delta H_2(t)$, $\Delta H_3(t)$. Wykonamy symulacje dla czterech zestawów warunków początkowych. Warunki początkowe dla przyrostów zmiennych stanu wynoszą

•  $\Delta H_1(t_0) = 0.2$, $\Delta H_2(t_0) = -0.2$, $\Delta H_3(t_0) = 0$
• $\Delta H_1(t_0) = 0.1$, $\Delta H_2(t_0) = -0.1$, $\Delta H_3(t_0) = 0$
•  $\Delta H_1(t_0) = 0.04$, $\Delta H_2(t_0) = -0.04$, $\Delta H_3(t_0) = 0$
•  $\Delta H_1(t_0) = 0.02$, $\Delta H_2(t_0) = -0.02$, $\Delta H_3(t_0) = 0$

Warunki początkowe dla zmiennych przyrostowych zmniejszają się proporcjonalnie dla kolejnych zestawów. Spodziewamy się, że dla coraz mniejszych początkowych przyrostów, trajektorie zmiennych stanu obiektu zlinearyzowanego będą coraz lepiej przybliżać trajektorie przyrostów stanu obiektu nieliniowego. Zgodnie z (1.222)-(1.224}) warunki początkowe dla modelu zlinearyzowanego wynoszą

$\begin{equation} \tilde{H}_1(t_0) = \Delta H_1(t_0),\ \tilde{H}_2(t_0) = \Delta H_2(t_0),\ \tilde{H}_3(t_0) = \Delta H_3(t_0) \end{equation}\qquad(1.245)$

Na Rys. 1.12 przedstawiono porównanie trajektorii zmiennej przyrostowej $\Delta H_3(t)$ obiektu nieliniowego i zmiennej $\tilde{H}_3(t)$ obiektu zlinearyzowanego dla ww. zestawów warunków początkowych. Wyraźnie widzimy, że im bliżej punktu równowagi w chwili początkowej znajduje się obiekt, tym lepiej zmienna $\tilde{H}_3(t)$ przybliża przebieg zmiennej $\Delta H_3(t)$.

W drugim scenariuszu zakładamy, że w chwili początkowej obiekt znajduje się w punkcie równowagi. Taka sytuacja odpowiada zerowym warunkom początkowym

$\begin{equation} \tilde{H}_1(t_0) = \Delta H_1(t_0) = 0,\ \tilde{H}_2(t_0) = \Delta H_2(t_0) = 0,\ \tilde{H}_3(t_0) = \Delta H_3(t_0) = 0 \end{equation}\qquad(1.246)$

Badamy teraz zachowanie układu w odpowiedzi na zmienne sterowanie $Q_{we}(t)$. Porównajmy trajektorie obiektu nieliniowego i zlinearyzowanego dla sygnału sterującego typu fala prostokątna oscylującego wokół wartości w punkcie równowagi $Q_{we0}=0.5$. Wypełnienie fali wynosi 50%, natomiast jej okres wynosi 2. Amplituda wahań fali prostokątnej dla czterech testowanych przypadków wynosi odpowiednio 0.25, 0.125, 0.05, 0.025.  

Sterowanie obiektu zlinearyzowanego w każdym przypadku wynosi

$\begin{equation} \tilde{Q}_{we}(t) = Q_{we}(t)-Q_{we0} \end{equation}\qquad(1.247)$

a) $\Delta H_1(t_0) = 0.2$, $\Delta H_2(t_0) = -0.2$, $\Delta H_3(t_0) = 0$ 

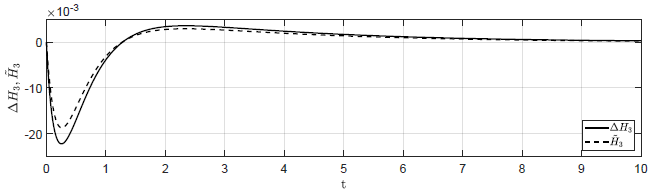
b) $\Delta H_1(t_0) = 0.1$, $\Delta H_2(t_0) = -0.1$, $\Delta H_3(t_0) = 0$

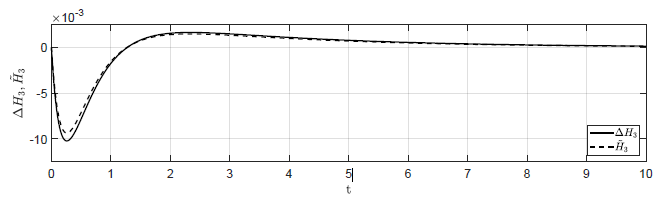
c) (\Delta H_1(t_0) = 0.04 \), $\Delta H_2(t_0) = -0.04$, $\Delta H_3(t_0) = 0$

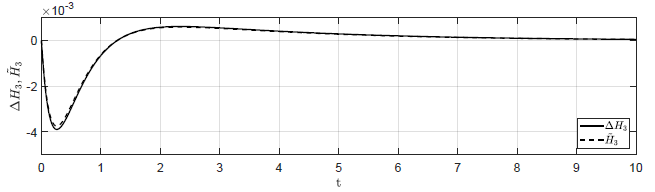
d) $\Delta H_1(t_0) = 0.02$, $\Delta H_2(t_0) = -0.02$, $\Delta H_3(t_0) = 0$

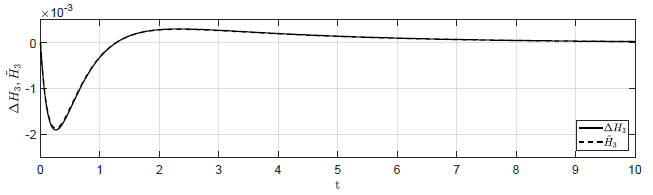
Rysunek 1.12 Porównanie trajektorii $\Delta H_3(t)$ obiektu nieliniowego oraz trajektorii $\tilde{H}_3(t)$ obiektu zlinearyzowanego w odpowiedzi na niezerowe warunki początkowe.

a) Amplituda fali prostokątnej 0.25

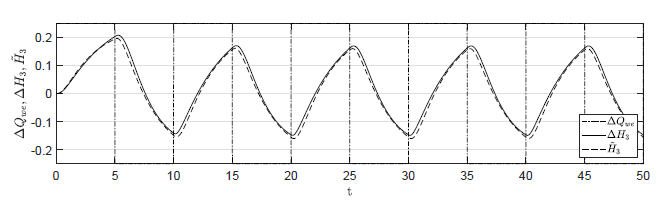
b) Amplituda fali prostokątnej 0.125

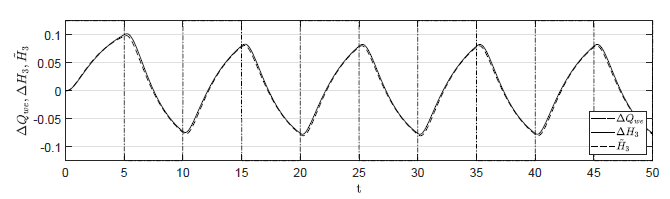
c) Amplituda fali prostokątnej 0.05

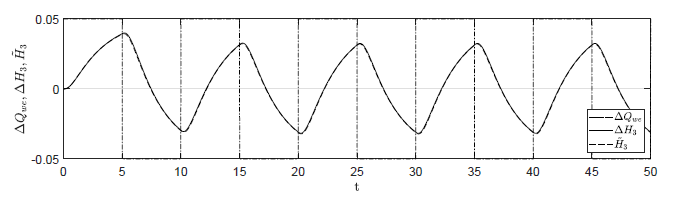
d) Amplituda fali prostokątnej 0.025

Rysunek 1.13 Porównanie trajektorii $\Delta H_3(t)$ obiektu nieliniowego oraz trajektorii $\tilde{H}_3(t)$ obiektu zlinearyzowanego w odpowiedzi na sygnał sterujący typu fala prostokątna.}

Spodziewamy się, że im mniejsza będzie amplituda zmian sygnału sterującego, tym lepiej trajektorie zmiennych stanu obiektu zlinearyzowanego będą przybliżać trajektorie przyrostów stanu obiektu nieliniowego. Na Rys. 1.13  przedstawiono porównanie trajektorii zmiennej przyrostowej \( \Delta H_3(t) \( obiektu nieliniowego i zmiennej $\tilde{H}_3(t)$ obiektu zlinearyzowanego dla sygnałów sterujących w kształcie fali prostokątnej o zmniejszającej się amplitudzie. Wyraźnie widzimy, że im mniejsza jest amplituda sygnału sterującego, tym lepiej zmienna $\tilde{H}_3(t)$ przybliża przebieg zmiennej $\Delta H_3(t)$.