Podręcznik
3. Linearyzacja równań modelu obiektu
3.4. Przykład 2 linearyzacji równań modelu obiektu
Wyprowadźmy teraz zlinearyzowane równania stanu dla wahadła. Przypomnijmy równania stanu dla wahadła
\( \begin{eqnarray} \frac{d\theta(t)}{dt} &=& \omega(t) \qquad(1.248)\\ \frac{d\omega(t)}{dt} &=& \frac{g}{l}sin\theta(t) - \frac{D}{ml^2} \omega(t) +\frac{1}{ml^2} M(t) \qquad(1.249) \end{eqnarray} \)
Funkcja prawych stron z pierwszego równania stanu ma postać
\( \begin{equation} f_1(\theta, \omega, M) = \omega \end{equation}\qquad(1.250) \)
Dla skrócenia zapisu pomijamy w zapisie argument czasu \( (t) \).
Rozwinięcie funkcji \( f_1 \) w szereg Taylora wokół punktu równowagi \( (\theta_0, \omega_0, M_0) \) ma postać
\( \begin{eqnarray} f_1(\theta, \omega, M) &\simeq& f_1(\theta_0, \omega_0, M_0) + \frac{\partial f_1(\theta_0, \omega_0, M_0)}{\partial \theta} (\theta-\theta_0) \\ &&+ \frac{\partial f_1(\theta_0, \omega_0, M_0)}{\partial \omega} (\omega-\omega_0) + \frac{\partial f_1(\theta_0, \omega_0, M_0)}{\partial M} (M-M_0) \qquad(1.251) \end{eqnarray} \)
Obliczmy wartości pochodnych cząstkowych funkcji \( f_1 \) względem zmiennych stanu i sterowań w punkcie równowagi
\( \begin{eqnarray} \frac{\partial f_1(\theta_0, \omega_0, M_0)}{\partial \theta} &=& 0 \qquad(1.252)\\ \frac{\partial f_1(\theta_0, \omega_0, M_0)}{\partial \omega} &=& 1 \qquad(1.253)\\ \frac{\partial f_1(\theta_0, \omega_0, M_0)}{\partial M} &=& 0\qquad(1.254) \end{eqnarray} \)
Rozwinięcie funkcji \( f_1 \) w szereg Taylora wynosi zatem
\( \begin{equation} f_1(\theta, \omega, M) \simeq \omega_0 + 0 \cdot (\theta-\theta_0) + 1 \cdot (\omega-\omega_0) + 0 \cdot (M-M_0) \end{equation}\qquad(1.255) \)
Funkcja prawych stron z drugiego równania stanu ma postać
\( \begin{equation} f_2(\theta, \omega, M) = \frac{g}{l}sin\theta - \frac{D}{ml^2} \omega +\frac{1}{ml^2} M \end{equation}\qquad(1.256) \)
Rozwinięcie funkcji \( f_2 \) w szereg Taylora wokół punktu równowagi \( (\theta_0, \omega_0, M_0) \) ma postać
\( \begin{eqnarray} f_2(\theta, \omega, M) &\simeq& f_2(\theta_0, \omega_0, M_0) + \frac{\partial f_2(\theta_0, \omega_0, M_0)}{\partial \theta} (\theta-\theta_0) \\ &&+ \frac{\partial f_2(\theta_0, \omega_0, M_0)}{\partial \omega} (\omega-\omega_0) + \frac{\partial f_2(\theta_0, \omega_0, M_0)}{\partial M} (M-M_0) \qquad(1.257) \end{eqnarray} \)
Obliczmy wartości pochodnych cząstkowych funkcji \( f_2 \) względem zmiennych stanu i sterowań w punkcie równowagi
\( \begin{eqnarray} \frac{\partial f_2(\theta_0, \omega_0, M_0)}{\partial \theta} &=& \frac{g}{l}cos\theta_0 \qquad(1.258)\\ \frac{\partial f_2(\theta_0, \omega_0, M_0)}{\partial \omega} &=& -\frac{D}{ml^2} \qquad(1.259)\\ \frac{\partial f_2(\theta_0, \omega_0, M_0)}{\partial M} &=& \frac{1}{ml^2}\qquad(1.260) \end{eqnarray} \)
Rozwinięcie funkcji \( f_2 \) w szereg Taylora wynosi zatem
\( \begin{eqnarray} f_2(\theta, \omega, M) &\simeq& \frac{g}{l}sin\theta_0 - \frac{D}{ml^2} \omega_0 +\frac{1}{ml^2} M_0 + \frac{g}{l}cos\theta_0 (\theta-\theta_0) \\ && - \frac{D}{ml^2} (\omega-\omega_0) + \frac{1}{ml^2} (M-M_0) \nonumber \end{eqnarray}\qquad(1.261) \)
Obliczyliśmy rozwinięcia w szereg Taylora wszystkich funkcji prawych stron. Przepiszmy zatem jeszcze raz równania stanu, ale zamiast funkcji użyjmy przybliżeń wynikających z szeregu Taylora
\( \begin{eqnarray} \frac{d\theta}{dt} &\simeq& \omega_0 + 0 \cdot (\theta-\theta_0) + 1 \cdot (\omega-\omega_0) + 0 \cdot (M-M_0) \\ \frac{d\omega}{dt} &\simeq& \frac{g}{l}sin\theta_0 - \frac{D}{ml^2} \omega_0 +\frac{1}{ml^2} M_0 + \frac{g}{l}cos\theta_0 (\theta-\theta_0) \qquad(1.262)\\ &&- \frac{D}{ml^2} (\omega-\omega_0) + \frac{1}{ml^2} (M-M_0) \\qquad(1.263) \end{eqnarray} \)
Zauważmy, że na podstawie warunków na punkt równowagi następujące wyrażenia zerują się
\( \begin{eqnarray} 0 &=& f_1(\theta_0, \omega_0, M_0) = \omega_0 \qquad(1.264)\\ 0 &=& f_2(\theta_0, \omega_0, M_0)= \frac{g}{l}sin\theta_0 - \frac{D}{ml^2} \omega_0 +\frac{1}{ml^2} M_0\qquad(1.265) \end{eqnarray} \)
Wynika z tego, że możemy pominąć wyrazy stałe w rozwinięciu w szereg Taylora
\( \begin{eqnarray} \frac{d\theta}{dt} &\simeq& 0 \cdot (\theta-\theta_0) + 1 \cdot (\omega-\omega_0) + 0 \cdot (M-M_0) \qquad(1.266)\\ \frac{d\omega}{dt} &\simeq& \frac{g}{l}cos\theta_0 (\theta-\theta_0) - \frac{D}{ml^2} (\omega-\omega_0) + \frac{1}{ml^2} (M-M_0)\qquad(1.267) \end{eqnarray} \)
Wprowadźmy następujące oznaczenia
\( \begin{eqnarray} \Delta \theta &=& \theta-\theta_0\qquad(1.268)\\ \Delta \omega &=& \omega-\omega_0\qquad(1.269)\\ \Delta M &=& M-M_0\qquad(1.270) \end{eqnarray} \)
Zmienne \( \Delta \theta \), \( \Delta \omega \) oraz \( \Delta M \) określają przyrosty wartości \( \theta \), \( \omega \) oraz \( M \) w stosunku do ich wartości w punkcie pracy \( \theta_0 \), \( \omega_0 \) oraz \( M_0 \). Możemy teraz zapisać przybliżenia w równaniach stanu jako
\( \begin{eqnarray} \frac{d\theta}{dt} &\simeq& 0 \cdot \Delta \theta + 1 \cdot \Delta \omega + 0 \cdot \Delta M \qquad(1.271)\\ \frac{d\omega}{dt} &\simeq& \frac{g}{l}cos\theta_0 \Delta \theta - \frac{D}{ml^2} \Delta \omega + \frac{1}{ml^2} \Delta M \qquad(1.272) \end{eqnarray} \)
Pochodne zmiennych przyrostowych \(\Delta \theta\) oraz \( \Delta \omega \) są równe pochodnym zmiennych oryginalnych
\( \begin{eqnarray} \frac{d\Delta \theta}{dt} &=& \frac{d (\theta-\theta_0)}{dt} = \frac{d \theta}{dt} - \frac{d \theta_0}{dt} = \frac{d \theta}{dt} \qquad(1.273)\\ \frac{d\Delta \omega}{dt} &=& \frac{d (\omega-\omega_0)}{dt} = \frac{d \omega}{dt} - \frac{d \omega_0}{dt} = \frac{d \omega}{dt}\qquad(1.274) \end{eqnarray} \)
Wprowadźmy zatem do przybliżeń wielkości \( \frac{d\Delta \theta}{dt} \) oraz \( \frac{d\Delta \omega}{dt} \) zamiast \( \frac{d \theta}{dt} \) oraz \( \frac{d \omega}{dt} \).
\( \begin{eqnarray} \frac{d\Delta \theta}{dt} &\simeq& 0 \cdot \Delta \theta + 1 \cdot \Delta \omega + 0 \cdot \Delta M \qquad(1.275)\\ \frac{d\Delta \omega}{dt} &\simeq& \frac{g}{l}cos\theta_0 \Delta \theta - \frac{D}{ml^2} \Delta \omega + \frac{1}{ml^2} \Delta M \qquad(1.276) \end{eqnarray} \)
Powyższe zależności są spełnione w przybliżeniu. Aby utworzyć równania zlinearyzowane wprowadzamy nowe wielkości \( \tilde{\theta} \), \( \tilde{\omega} \), oraz \( \tilde{M} \) oraz definiujemy równania zlinearyzowane w następujący sposób
\( \begin{eqnarray} \frac{d\tilde{\theta}}{dt} &=& 0 \cdot \tilde{\theta} + 1 \cdot \tilde{\omega} + 0 \cdot \tilde{M} \qquad(1.277) \\ \frac{d\tilde{\omega}}{dt} &=& \frac{g}{l}cos\theta_0 \tilde{\theta} - \frac{D}{ml^2} \tilde{\omega} + \frac{1}{ml^2} \tilde{M} \qquad(1.278) \end{eqnarray} \)
Są to równania w ścisłym sensie, gdyż zamiast znaku przybliżenia \( \simeq \) pojawia się znak równości. Postulujemy, że jeżeli zachodzą następujące warunki
- w pewnym ustalonym przedziale czasu \( t\in [ t_0, t_1 ] \) funkcja sterowań \( \tilde{M}(t) \) jest dokładnie równa przyrostowi zmiennej \( M(t) \)
\( \begin{equation} \tilde{M}(t) = \Delta M(t) = M(t)-M_0 \qquad(1.279) \end{equation} \)
- warunki początkowe dla zmiennych \( \tilde{\theta} \), \( \tilde{\omega} \) są dokładnie równe przyrostom zmiennych \( \theta \) oraz \( \omega \) w chwili początkowej
\( \begin{eqnarray} \tilde{\theta}(t_0) &= &\Delta \theta(t_0) = \theta(t_0) - \theta_0 \qquad(1.280) \\ \tilde{\omega}(t_0) &= &\Delta \omega(t_0) = \omega(t_0) - \omega_0 \qquad(1.281) \end{eqnarray} \)
- w pewnym ustalonym przedziale czasu \( t\in [ t_0, t_1 ] \) rozwiązania nieliniowych równań stanu \( \theta(t) \) oraz \( \omega(t) \) pozostają w otoczeniu punktu równowagi \( (\theta_0, \omega_0) \) (\( C_{\theta}, C_{\omega} \) -- stałe dodatnie)
\( \begin{eqnarray} | \theta(t)-\theta_0 | &=& | \Delta \theta(t) | \leq C_{\theta} \qquad(1.282) \\ | \omega(t)-\omega_0 | &=& | \Delta \omega(t) | \leq C_{\omega} \qquad(1.282) \end{eqnarray} \)
to rozwiązania \( \tilde{\theta}(t) \) oraz \( \tilde{\omega}(t) \) liniowych równań stanu (1.277)-(1.278) dobrze przybliżają przyrosty zmiennych stanu dla \( t\in [ t_0, t_1 ] \) tzn. w tym przedziale czasu zachodzą przybliżone warunki
\( \begin{eqnarray} \tilde{\theta}(t) &\simeq& \Delta \theta(t) \qquad(1.284)\\ \tilde{\omega}(t) &\simeq& \Delta \omega(t) \qquad(1.285) \end{eqnarray} \)
Przybliżenie to jest tym lepsze im bliżej wybranego punktu równowagi pozostają rozwiązania nieliniowych równań stanu tzn. im mniejsze są stałe \( C_{\theta}, C_{\omega} \) w równaniach (1.282)-(1.283).
Funkcja wyjść dla wahadła ma postać
\( \begin{equation} y_1 = g_1(\theta,\omega) = \theta \end{equation}\qquad(1.286) \)
Linearyzacja funkcji wyjść ma postać
\( \begin{equation} g_1(\theta,\omega) \simeq g_1(\theta_0,\omega_0) + \frac{\partial g_1(\theta_0,\omega_0)}{\partial \theta} (\theta-\theta_0) + \frac{\partial g_1(\theta_0,\omega_0)}{\partial \omega} (\omega-\omega_0) \end{equation}\qquad(1.287) \)
Wartości pochodnych cząstkowych funkcji \( g_1 \) względem zmiennych stanu i sterowań w punkcie równowagi wynoszą
\( \begin{eqnarray} \frac{\partial g_1(\theta_0,\omega_0)}{\partial \theta} &=& 1 \qquad(1.288)\\ \frac{\partial g_1(\theta_0,\omega_0)}{\partial \omega} &=& 0 \qquad(1.289) \end{eqnarray} \)
Rozwinięcie funkcji wyjść w szereg Taylora wynosi zatem
\( \begin{equation} y_1 \simeq y_{10} + 1 \cdot (\theta-\theta_0)+ 0 \cdot (\omega-\omega_0) \end{equation}/qquad(1.290) \)
gdzie \( y_{10} = g_1(\theta_0,\omega_0) \).
Jeżeli przeniesiemy \( y_{10} \) na drugą stronę przybliżenia dostajemy
\( \begin{equation} y_1- y_{10} \simeq 1 \cdot (\theta-\theta_0)+ 0 \cdot (\omega-\omega_0) \end{equation}\qquad(1.291) \)
Jeżeli teraz wprowadzimy do przybliżenia zmienne przyrostowe, to otrzymujemy
\( \begin{equation} \Delta y_1 \simeq 1 \cdot \Delta \theta + 0 \cdot \Delta \omega \end{equation}\qquad(1.292) \)
gdzie
\( \begin{equation} \Delta y_1 = y_1-y_{10} \end{equation}\qquad(1.293) \)
Aby zdefiniować zlinearyzowane równanie wyjść wprowadzamy zmienną \( \tilde{y}_1 \). Zlinearyzowane równanie wyjść ma postać
\( \begin{equation} \tilde{y}_1 = 1 \cdot \tilde{\theta} + 0 \cdot \tilde{\omega} \end{equation}\qquad(1.294) \)
Postulując takie same warunki jak w przypadku równań stanu oczekujemy, że rozwiązanie równania wyjść \( \tilde{y}_1 \) będzie dobrze przybliżać przyrost zmiennej wyjściowej \( y_1 \)
\( \begin{equation} \tilde{y}_1 \simeq \Delta y_1 = y_1-y_{10} \end{equation}\qquad(1.295) \)
Zlinearyzowane równania stanu i wyjść mogą zostać przedstawione w postaci wektorowej
\( \begin{equation} \left( \begin{array}{c} \frac{d\tilde{\theta}}{dt}\\ \frac{d\tilde{\omega}}{dt} \end{array} \right) = \left( \begin{array}{cc} 0 & 1 \\ \frac{g}{l}cos\theta_0 & -\frac{D}{ml^2} \end{array} \right) \left( \begin{array}{c} \tilde{\theta}\\ \tilde{\omega} \end{array} \right) + \left( \begin{array}{c} 0 \\ \frac{1}{ml^2} \end{array} \right) \left( \tilde{M} \right) \end{equation}\qquad(1.296) \)
\( \begin{eqnarray} \left( y_1 \right) &=& \left( \begin{array}{cc} 1 & 0 \end{array} \right) \left( \begin{array}{c} \tilde{\theta}\\ \tilde{\omega} \end{array} \right) \end{eqnarray}\qquad(1.297) \)
Aby przetestować zdolność modelu zlinearyzowanego do przybliżania dynamiki obiektu nieliniowego porównajmy przebiegi czasowe zmiennych stanu dla obu modeli. Przyjmujemy parametry obiektu \( m = 0.1 \), \( l = 1 \), \( g = 10 \), \( D = 0.1 \). Wybieramy punkt równowagi odpowiadający \( \theta_0=\frac{5\pi}{6} \), \( \omega_0=0 \) oraz \( M_{0} = -0.5 \). W pierwszym scenariuszu zakładamy, że w chwili początkowej obiekt nie znajduje się w punkcie równowagi.
Ponadto przyjmujemy, że sterowanie obiektu jest stałe i równe sterowaniu w punkcie równowagi \( M(t) = M_0\). Ze wzoru (1.279) wynika, że sterowanie obiektu zlinearyzowanego wynosi
\( \begin{equation} \tilde{M}(t) = M(t)-M_0 = M_0-M_0=0 \end{equation}\qquad(1.298) \)
Zmienne stanu obiektu zlinearyzowanego \( \tilde{\theta}(t) \), oraz \( \tilde{\omega}(t) \) przybliżają przyrosty zmiennych stanu obiektu nieliniowego \( \Delta \theta \), \( \Delta \omega \). Wykonamy symulacje dla czterech zestawów warunków początkowych. Warunki początkowe dla przyrostów zmiennych stanu wynoszą
- \(\Delta \theta(t_0) = -\frac{\pi}{3} \), \( \Delta \omega(t_0) = -1 \)
- \(\Delta \theta(t_0) = -\frac{\pi}{6} \), \( \Delta \omega(t_0) = -0.5 \)
- \(\Delta \theta(t_0) = -\frac{\pi}{15} \), \( \Delta \omega(t_0) = -0.2 \)
- \(\Delta \theta(t_0) = -\frac{\pi}{30} \), \( \Delta \omega(t_0) = -0.1 \)
Warunki początkowe dla zmiennych przyrostowych zmniejszają się proporcjonalnie dla kolejnych zestawów. Spodziewamy się, że dla coraz mniejszych początkowych przyrostów, trajektorie zmiennych stanu obiektu zlinearyzowanego będą coraz lepiej przybliżać trajektorie przyrostów stanu obiektu nieliniowego. Zgodnie z (1.280})-(1.281) warunki początkowe dla modelu zlinearyzowanego wynoszą
\( \begin{equation} \tilde{\theta}(t_0) = \Delta \theta(t_0),\ \tilde{\omega}(t_0) = \Delta \omega(t_0) \end{equation}\qquad(1.299) \)
Na Rys. 1.14 przedstawiono porównanie trajektorii zmiennej przyrostowej \( \Delta \theta(t) \) obiektu nieliniowego i zmiennej \( \tilde{\theta}(t) \) obiektu zlinearyzowanego dla ww. zestawów warunków początkowych. Wyraźnie widzimy, że im bliżej punktu równowagi w chwili początkowej znajduje się obiekt, tym lepiej zmienna \( \tilde{\theta}(t) \) przybliża przebieg zmiennej \( \Delta \theta(t)\).
a) \(\Delta \theta(t_0) = -\frac{\pi}{3} \), \( \Delta \omega(t_0) = -1 \)
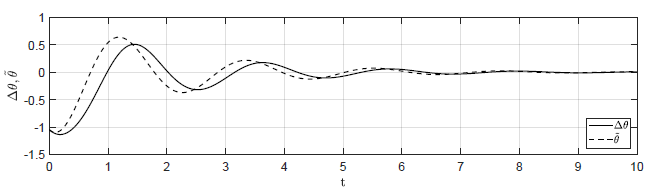
b) \(\Delta \theta(t_0) = -\frac{\pi}{6} \), \( \Delta \omega(t_0) = -0.5 \)

c) \(\Delta \theta(t_0) = -\frac{\pi}{15} \), \( \Delta \omega(t_0) = -0.2\)

d) \(\Delta \theta(t_0) = -\frac{\pi}{30} \), \( \Delta \omega(t_0) = -0.1 \)
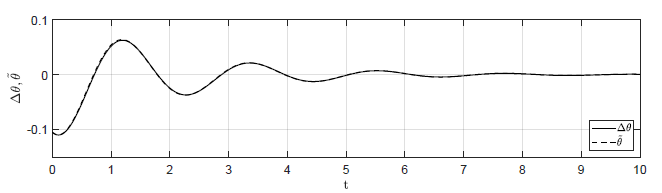
Rysunek 1.14 Porównanie trajektorii \( \Delta \theta(t) \) obiektu nieliniowego oraz trajektorii \( \tilde{\theta}(t) \) obiektu zlinearyzowanego w odpowiedzi na niezerowe warunki początkowe.
Wartości sterowania \( M_{0} = -0.5 \) odpowiada także drugi punkt równowagi \( \theta_0=\frac{\pi}{6} \), \( \omega_0=0 \). Ponownie wykonujemy symulacje dla czterech zestawów warunków początkowych. Warunki początkowe dla przyrostów zmiennych stanu wynoszą
- \(\Delta \theta(t_0) = \frac{\pi}{3} \), \( \Delta \omega(t_0) = -1 \)
- \(\Delta \theta(t_0) = \frac{\pi}{30} \), \( \Delta \omega(t_0) = -0.1 \)
- \(\Delta \theta(t_0) = \frac{\pi}{300} \), \( \Delta \omega(t_0) = -0.01 \)
- \(\Delta \theta(t_0) = \frac{\pi}{3000} \), \( \Delta \omega(t_0) = -0.001 \)
Warunki początkowe dla zmiennych przyrostowych zmniejszają się proporcjonalnie dla kolejnych zestawów. Zgodnie z (1.280)-(1.281) warunki początkowe dla modelu zlinearyzowanego wynoszą
\( \begin{equation} \tilde{\theta}(t_0) = \Delta \theta(t_0),\ \tilde{\omega}(t_0) = \Delta \omega(t_0) \end{equation}\qquad(1.300) \)
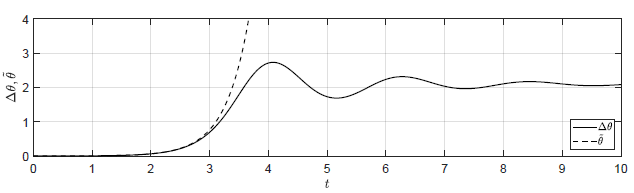
Na Rys. 1.15 przedstawiono porównanie trajektorii zmiennej przyrostowej \( \Delta \theta(t) \) obiektu nieliniowego i zmiennej \( \tilde{\theta}(t) \) obiektu zlinearyzowanego dla ww. zestawów warunków początkowych. Tym razem zachowanie obiektu nieliniowego i zlinearyzowanego są diametralnie różne. Dla każdego zestawu warunków początkowych wahadło najpierw spada (\( \theta(t) \) rośnie), następnie wykonuje oscylacje wokół położenia kątowego \( \theta = \frac{5\pi}{6} \), by wreszcie ustabilizować się w tym położeniu. Niezależnie od tego jak blisko położenia równowagi \( \theta_0 = \frac{\pi}{6} \) znajduje się obiekt w chwili początkowej, wahadło trwale oddala się od tego położenia i stabilizuje się w innym położeniu równowagi. Trajektoria \( \tilde{\theta}(t) \) z kolei rośnie w bardzo szybkim tempie (jak funkcja \( e^t \)) i nie wykazuje żadnych drgań.
Różnica pomiędzy zachowaniem obiektu nieliniowego i zlinearyzowanego w tym przypadku wynika z niespełnienia warunków (1.282)-(1.283) na rozważanym horyzoncie czasu. Trajektorie zmiennych stanu trwale oddalają się od pierwotnego punktu równowagi niezależnie od tego jak blisko punktu równowagi znajdują się warunki początkowe.
Zauważmy jednak, że dla początkowego przedziału czasu, gdy trajektorie zmiennych stanu znajdują się jeszcze blisko punktu równowagi, trajektorie modelu zlinearyzowanego dobrze przybliżają trajektorie modelu nieliniowego. Jest to bardzo ważna cecha linearyzacji. Dopóki nie oddalamy się zbytnio od punktu równowagi, model zlinearyzowany dobrze przybliża zachowanie modelu nieliniowego. Jeżeli jednak oddalimy się zbytnio od punktu równowagi, wtedy nie możemy oczekiwać od modelu zlinearyzowanego dobrego przybliżenia dynamiki modelu nieliniowego. Oba modele mogą w takiej sytuacji dawać kompletnie odmienne rezultaty.
W drugim scenariuszu zakładamy, że w chwili początkowej obiekt znajduje się w punkcie równowagi \( \theta_0=\frac{5\pi}{6} \), \( \omega_0=0 \) oraz \( M_{0} = -0.5 \). Taka sytuacja odpowiada zerowym warunkom początkowym
\( \begin{equation} \tilde{\theta}(t_0) = \Delta \theta(t_0) = 0,\ \tilde{\omega}(t_0) = \Delta \omega(t_0) = 0 \end{equation}\qquad(1.301) \)
a) \(\Delta
\theta(t_0) = \frac{\pi}{3} \), \( \Delta \omega(t_0) = -1 \)
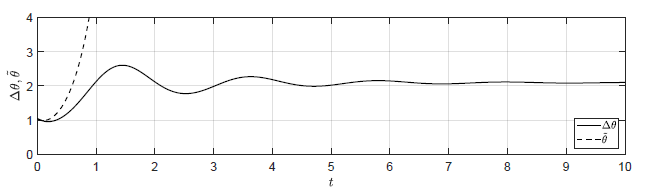
b) \(\Delta \theta(t_0) = \frac{\pi}{30} \), \( \Delta \omega(t_0) = -0.1 \)
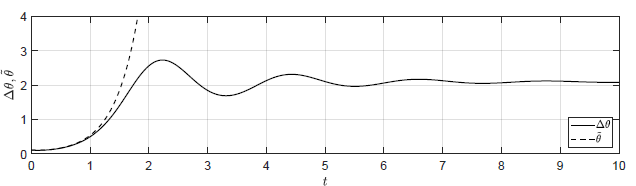
c) \(\Delta \theta(t_0) = \frac{\pi}{300} \), \( \Delta \omega(t_0) = -0.01 \)

d) \(\Delta \theta(t_0) = \frac{\pi}{3000} \), \( \Delta \omega(t_0) = -0.001 \)
Rysunek 1.5 Porównanie trajektorii \( \Delta \theta(t) \) obiektu nieliniowego oraz trajektorii \( \tilde{\theta}(t) \) obiektu zlinearyzowanego w odpowiedzi na niezerowe warunki początkowe.
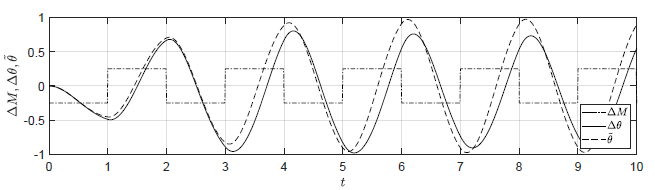
a) Amplituda fali prostokątnej 0.25
b) Amplituda fali prostokątnej 0.125

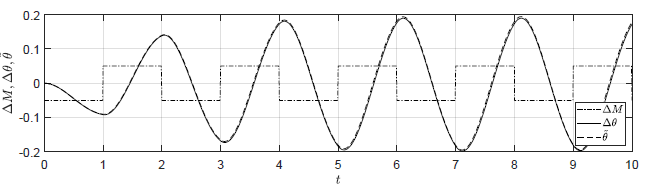
c) Amplituda fali prostokątnej 0.05
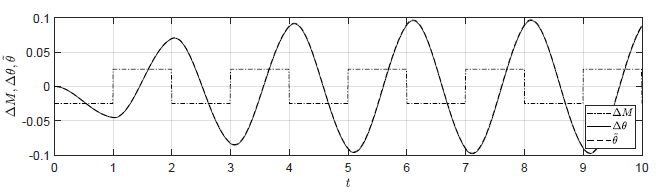
d) Amplituda fali prostokątnej 0.025
Rysunek 1.16 Porównanie trajektorii \( \Delta H_3(t) \) obiektu nieliniowego oraz trajektorii \( \tilde{H}_3(t) \) obiektu zlinearyzowanego w odpowiedzi na sygnał sterujący typu fala prostokątna.
Badamy teraz zachowanie układu w odpowiedzi na zmienne sterowanie \( M(t)\). Porównajmy trajektorie obiektu nieliniowego i zlinearyzowanego dla sygnału sterującego typu fala prostokątna oscylującego wokół wartości w punkcie równowagi \( M_0=-0.5 \). Wypełnienie fali wynosi 50%, natomiast jej okres wynosi 2. Amplituda wahań fali prostokątnej dla czterech testowanych przypadków wynosi odpowiednio 0.25, 0.125, 0.05, 0.025.
Sterowanie obiektu zlinearyzowanego w każdym przypadku wynosi
\( \begin{equation} \tilde{M}(t) = M(t)-M_{0} \end{equation}\qquad(1.302) \)
Na Rys. 1.16 przedstawiono porównanie trajektorii zmiennej przyrostowej \( \Delta \theta(t) \) obiektu nieliniowego i zmiennej \( \tilde{\theta}(t) \) obiektu zlinearyzowanego dla sygnałów sterujących w kształcie fali prostokątnej o zmniejszającej się amplitudzie. Tym razem trajektorie układu nieliniowego pozostają w pobliżu punktu równowagi na całym horyzoncie czasu. Im mniejsza jest amplituda sygnału sterującego, tym lepiej zmienna \( \tilde{\theta}(t) \) przybliża przebieg zmiennej \( \Delta \theta(t) \).
