Podręcznik

Rozważmy układ regulacji z regulatorem P dla układu trzech zbiorników. Opis nieliniowego układu regulacji składa się z nieliniowych równań stanu obiektu

$\begin{eqnarray} \dfrac{d H_1(t)}{dt} &=& \dfrac{1}{A}Q_{we}(t) - \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(2.15) \\ \dfrac{d H_2(t)}{dt} &=& \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \dfrac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(2.16) \\ \dfrac{d H_3(t)}{dt} &=& \dfrac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \dfrac{\alpha}{2A} \sqrt{H_3(t)} \qquad(2.17) \end{eqnarray}$

oraz równania regulatora P dla punktu pracy określonego przez  $H_{10}$, $H_{20}$, $H_{30}$ oraz $Q_{we0}$

$\begin{equation} Q_{we}(t) = k_p(H_3(t)-H_{30}) + Q_{we0} \qquad(2.18) \end{equation}$

Jeżeli wprowadzimy równanie regulatora P do równań stanu obiektu, to otrzymamy równania stanu układu regulacji

$\begin{eqnarray} \dfrac{d H_1(t)}{dt} &=& \dfrac{1}{A}\left(k_p(H_3(t)-H_{30}) + Q_{we0} \right) - \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(2.19)\\ \dfrac{d H_2(t)}{dt} &=& \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \dfrac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(2.20) \\ \dfrac{d H_3(t)}{dt} &=& \dfrac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \dfrac{\alpha}{2A} \sqrt{H_3(t)} \qquad(2.21) \end{eqnarray}$

Zauważmy, że w równaniach stanu układu regulacji formalnie nie występuje sygnał sterujący, sterowanie zależy bowiem jedynie od wyjścia układu $H_3(t)$ i od wartości $H_{30}$ oraz $Q_{we0}$, które są stałymi. Opis zlinearyzowanego układu regulacji składa się ze zlinearyzowanych równań stanu obiektu

$\begin{eqnarray} \dfrac{d\tilde{H}_1}{dt} &=& \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_2 + \dfrac{1}{A} \tilde{Q}_{we} \qquad(2.22) \\ \dfrac{d\tilde{H}_2}{dt} &=& \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \left( \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \dfrac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \right) \tilde{H}_2 \\ &&+ \dfrac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \tilde{H}_3 \qquad(2.23) \\ \dfrac{d\tilde{H}_3}{dt} &=& \dfrac{\alpha}{4A\sqrt{H_{20}-H_{30}}} \tilde{H}_2 + \left( \dfrac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \dfrac{-\alpha}{4A\sqrt{H_{30}}} \right) \tilde{H}_3 \qquad(2.24) \end{eqnarray}$

oraz zlinearyzowanego równania regulatora P. Zapiszmy równanie regulatora P w postaci przyrostowej

$\begin{equation} \Delta Q_{we}(t) = k_p \Delta H_3(t) \end{equation}\qquad(2.25)$

Powyższe równanie jest liniowe, zatem możemy natychmiast zapisać równanie zlinearyzowanego regulatora P jako 

$\begin{equation} \tilde{Q}_{we}(t) = k_p \tilde{H}_3(t) \end{equation}\qquad(2.26)$

Jeżeli wprowadzimy zlinearyzowane równanie regulatora P do zlinearyzowanych równań stanu obiektu, to otrzymamy zlinearyzowane równania stanu układu regulacji

$\begin{eqnarray} \dfrac{d\tilde{H}_1}{dt} &=& \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_2 + \dfrac{1}{A} k_p \tilde{H}_3(t) \qquad(2.27)\\ \dfrac{d\tilde{H}_2}{dt} &=& \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \left( \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \dfrac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \right) \tilde{H}_2 \nonumber \\ &&+ \dfrac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \tilde{H}_3 \qquad(2.28) \\ \dfrac{d\tilde{H}_3}{dt} &=& \dfrac{\alpha}{4A\sqrt{H_{20}-H_{30}}} \tilde{H}_2 + \left( \dfrac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \dfrac{-\alpha}{4A\sqrt{H_{30}}} \right) \tilde{H}_3 \qquad(2.29) \end{eqnarray}$

Powyższe równania stanu moglibyśmy także uzyskać poprzez bezpośrednią linearyzację równań stanu układu regulacji (2.19)-(2.21). Podobnie jak to było w przypadku linearyzacji równań obiektu, omówionych w poprzednim module, formułujemy następujący postulat.

Postulujemy, że jeżeli zachodzą następujące warunki  

• warunki początkowe dla zmiennych $\tilde{H}_1$, $\tilde{H}_2$, $\tilde{H}_3$ są dokładnie równe przyrostom zmiennych $H_1$, $H_2$ oraz $H_3$ w chwili początkowej

$\begin{eqnarray} \tilde{H}_1(t_0) &=& \Delta H_1(t_0) = H_1(t_0)-H_{10} \qquad(2.30) \\ \tilde{H}_2(t_0) &=& \Delta H_2(t_0) = H_2(t_0)-H_{20} \qquad(2.31) \\ \tilde{H}_3(t_0) &=& \Delta H_3(t_0) = H_3(t_0)-H_{30} \qquad(2.32) \end{eqnarray}$

• w pewnym ustalonym przedziale czasu $t\in [ t_0, t_1 ]$ rozwiązania $H_1(t)$, $H_2(t)$, $H_3(t)$ nieliniowych równań stanu układu regulacji (2.19)-(2.21)  pozostają w otoczeniu punktu pracy $(H_{10},  H_{20}, H_{30})$ ($C_{H_1}, C_{H_2}, C_{H_3}$ -- stałe dodatnie)

$\begin{eqnarray} | H_1(t)-H_{10} | &=& | \Delta H_1(t) | \leq C_{H_1} \qquad(2.33) \\ | H_2(t)-H_{20} | &=& | \Delta H_2(t) | \leq C_{H_2} \qquad(2.34)\\ | H_3(t)-H_{30} | &=& | \Delta H_3(t) | \leq C_{H_3} \qquad(2.35) \end{eqnarray}$

to rozwiązania $\tilde{H}_1(t)$, $\tilde{H}_2(t)$ oraz $\tilde{H}_3(t)$ liniowych równań stanu (2.27)-(2.29) dobrze przybliżają przyrosty zmiennych stanu dla $t\in [ t_0, t_1 ]$ tzn. w tym przedziale czasu zachodzi przybliżony warunek

$\begin{eqnarray} \tilde{H}_1(t) &\simeq& \Delta H_1(t) \qquad(2.36) \\ \tilde{H}_2(t) &\simeq& \Delta H_2(t) \qquad(2.37)\\ \tilde{H}_3(t) &\simeq& \Delta H_3(t) \qquad(2.38) \end{eqnarray}$

Przybliżenie to jest tym lepsze im bliżej wybranego punktu pracy pozostają rozwiązania nieliniowych równań stanu tzn. im mniejsze są stałe $C_{H_1}, C_{H_2}, C_{H_3}$ w równaniach (2.33)-(2.35).   

Aby przetestować zdolność zlinearyzowanego modelu układu regulacji do przybliżania dynamiki układu nieliniowego porównajmy przebiegi czasowe zmiennych stanu dla obu modeli. Przyjmujemy parametry obiektu $A = 0.5$, $\alpha = 1$. Wybieramy punkt pracy $H_{10}=0.75$, $H_{20}=0.5$ $H_{30}=0.25$ oraz $Q_{we0} = 0.5$. Przyjmujemy wzmocnienie regulatora $k_p =-2$. Zmienne stanu  zlinearyzowanego układu regulacji $\tilde{H}_1(t)$, $\tilde{H}_2(t)$ oraz $\tilde{H}_3(t)$ przybliżają przyrosty zmiennych stanu układu nieliniowego $\Delta H_1(t)$, $\Delta H_2(t)$, $\Delta H_3(t)$. Wykonamy symulacje dla czterech zestawów warunków początkowych. Warunki początkowe dla przyrostów zmiennych stanu wynoszą

• $\Delta H_1(t_0) = 0.2$, $\Delta H_2(t_0) = -0.2$, $\Delta H_3(t_0) = 0$

• $\Delta H_1(t_0) = 0.1$, $\Delta H_2(t_0) = -0.1$, $\Delta H_3(t_0) = 0$

• $\Delta H_1(t_0) = 0.04$, $\Delta H_2(t_0) = -0.04$, $\Delta H_3(t_0) = 0$

• $\Delta H_1(t_0) = 0.02$, $\Delta H_2(t_0) = -0.02$, $\Delta H_3(t_0) = 0$

Warunki początkowe dla zmiennych przyrostowych zmniejszają się proporcjonalnie dla kolejnych zestawów. Spodziewamy się, że dla coraz mniejszych początkowych przyrostów, trajektorie zmiennych stanu układu zlinearyzowanego będą coraz lepiej przybliżać trajektorie przyrostów stanu układu nieliniowego. Zgodnie z (2.30)-2.32) warunki początkowe dla modelu zlinearyzowanego wynoszą

$\begin{equation} \tilde{H}_1(t_0) = \Delta H_1(t_0),\ \tilde{H}_2(t_0) = \Delta H_2(t_0),\ \tilde{H}_3(t_0) = \Delta H_3(t_0) \end{equation}\qquad(2.39)$

a) $\Delta H_1(t_0) = 0.2$, $\Delta H_2(t_0) = -0.2$, $\Delta H_3(t_0) = 0$

b) $\Delta H_1(t_0) = 0.1$, $\Delta H_2(t_0) = -0.1$, $\Delta H_3(t_0) = 0$

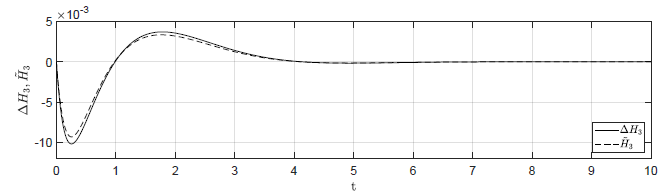
c) $\Delta H_1(t_0) = 0.04$, $\Delta H_2(t_0) = -0.04$, $\Delta H_3(t_0) = 0$

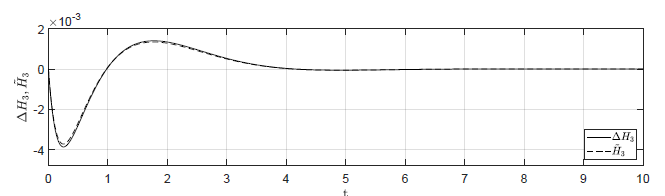
d) $\Delta H_1(t_0) = 0.02$, $\Delta H_2(t_0) = -0.02$, $\Delta H_3(t_0) = 0$

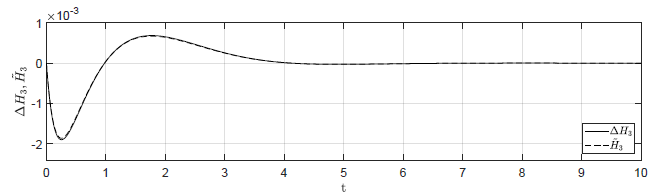
Rysunek 2.11 Porównanie trajektorii $\Delta H_3(t)$ nieliniowego układu regulacji oraz trajektorii $\tilde{H}_3(t)$ układu zlinearyzowanego w odpowiedzi na niezerowe warunki początkowe.

Na Rys.2.11 przedstawiono porównanie trajektorii zmiennej przyrostowej $\Delta H_3(t)$ nieliniowego układu regulacji i zmiennej $\tilde{H}_3(t)$ układu zlinearyzowanego dla ww. zestawów warunków początkowych. Wyraźnie widzimy, że im bliżej punktu pracy w chwili początkowej znajduje się układ regulacji, tym lepiej zmienna $\tilde{H}_3(t)$ przybliża przebieg zmiennej $\Delta H_3(t)$.

W przypadku regulatora nieliniowego o algorytmie 

$\begin{equation} Q_{we}(t) = Q_{we0} \left( e^{k_{nl} (H_3(t)-H_{30})} \right) \qquad(2.40) \end{equation}$

Równania stanu nieliniowego układu regulacji mają postać

$\begin{eqnarray} \dfrac{d\tilde{H}_1}{dt} &=& \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_2 + \dfrac{1}{A} Q_{we0} \left( e^{k_{nl} (H_3(t)-H_{30})} \right) \qquad(2.41)\\ \dfrac{d\tilde{H}_2}{dt} &=& \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \left( \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \dfrac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \right) \tilde{H}_2 \nonumber \\ &&+ \dfrac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \tilde{H}_3 \qquad(2.42)\\ \dfrac{d\tilde{H}_3}{dt} &=& \dfrac{\alpha}{4A\sqrt{H_{20}-H_{30}}} \tilde{H}_2 + \left( \dfrac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \dfrac{-\alpha}{4A\sqrt{H_{30}}} \right) \tilde{H}_3 \qquad(2.43) \end{eqnarray}$

Równanie regulatora nieliniowego zapisane przy pomocy przyrostów zmiennych ma postać

$\begin{equation} \Delta Q_{we}(t) = Q_{we0} \left( e^{k_{nl} \Delta H_3(t)} -1 \right) = r(\Delta H_3(t)) \qquad(2.44) \end{equation}$

Musimy teraz obliczyć rozwinięcie równania regulatora w szereg Taylora 

$\begin{equation} \Delta Q_{we}(t) = r(\Delta H_3(t)) \simeq r(\Delta H_{30}) + \dfrac{\partial r(\Delta H_{30})}{ \partial \Delta H_3} \Delta H_3(t) \end{equation} \qquad(2.45)$

Wartość przyrostu $\Delta H_{30}$ w punkcie pracy wynosi zero. Podobnie wartość funkcji regulatora w punkcie pracy $r(\Delta H_{30})$ wynosi zero.  Pochodna cząstkowa $\dfrac{\partial r(\Delta H_{30})}{ \partial \Delta H_3}$ obliczona w punkcie pracy wynosi 

$\begin{equation} \dfrac{\partial r(\Delta H_{30})}{ \partial \Delta H_3} = Q_{we0} k_{nl} e^{k_{nl} \Delta H_{30}} = Q_{we0} k_{nl} \end{equation}\qquad(2.46)$

Rozwinięcie równania regulatora w szereg Taylora ma zatem postać 

$\begin{equation} \Delta Q_{we}(t) = Q_{we0} k_{nl} \Delta H_3(t) \end{equation} \qquad(2.47)$

Zlinearyzowane równanie regulatora ma postać 

$\begin{equation} \tilde{Q}_{we}(t) = Q_{we0} k_{nl} \tilde{H}_3(t) \end{equation} \qquad(2.48)$

Jeżeli wprowadzimy zlinearyzowane równanie regulatora P do zlinearyzowanych równań stanu obiektu, to otrzymamy zlinearyzowane równania stanu układu regulacji

$\begin{eqnarray} \dfrac{d\tilde{H}_1}{dt} &=& \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_2 + \dfrac{1}{A} Q_{we0} k_{nl} \tilde{H}_3(t) \qquad(2.49) \\ \dfrac{d\tilde{H}_2}{dt} &=& \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} \tilde{H}_1 + \left( \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \dfrac{-\alpha}{2A\sqrt{H_{20}-H_{30}}} \right) \tilde{H}_2 \nonumber \\ &&+ \dfrac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \tilde{H}_3 \qquad(2.50)\\ \dfrac{d\tilde{H}_3}{dt} &=& \dfrac{\alpha}{4A\sqrt{H_{20}-H_{30}}} \tilde{H}_2 + \left( \dfrac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} + \dfrac{-\alpha}{4A\sqrt{H_{30}}} \right) \tilde{H}_3 \qquad(2.51) \end{eqnarray}$

a) $\Delta H_1(t_0) = 0.2$, $\Delta H_2(t_0) = -0.2$, $\Delta H_3(t_0) = 0$

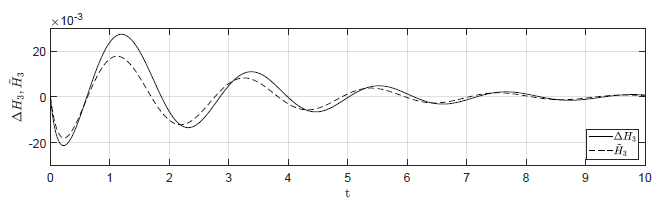
b) $\Delta H_1(t_0) = 0.1$, $\Delta H_2(t_0) = -0.1$, $\Delta H_3(t_0) = 0$

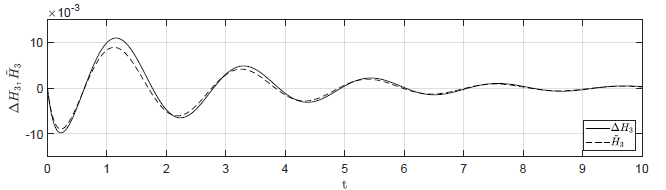
c) $\Delta H_1(t_0) = 0.04$, $\Delta H_2(t_0) = -0.04$, $\Delta H_3(t_0) = 0$

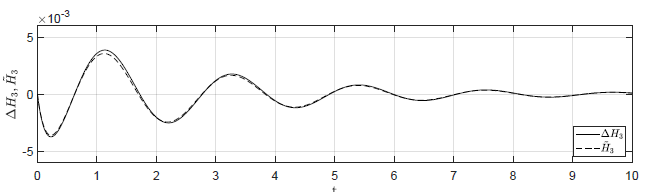
d) $\Delta H_1(t_0) = 0.02$, $\Delta H_2(t_0) = -0.02$, $\Delta H_3(t_0) = 0$

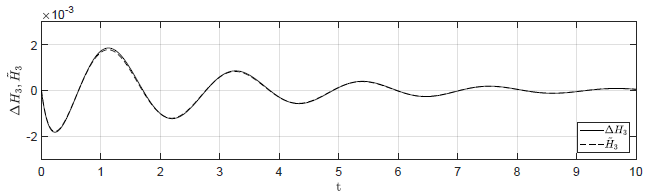
Rysunek 2.12 Porównanie trajektorii $\Delta H_3(t)$ nieliniowego układu regulacji oraz trajektorii $\tilde{H}_3(t)$ układu zlinearyzowanego w odpowiedzi na niezerowe warunki początkowe.

Przyjmujemy analogiczne postulaty, jak w przypadku układu regulacji z regulatorem P. Na Rys. 2.12 przedstawiono porównanie trajektorii zmiennej przyrostowej $\Delta H_3(t)$ nieliniowego układu regulacji i zmiennej $\tilde{H}_3(t)$ układu zlinearyzowanego dla takich samych warunków początkowych jak w przypadku układu z regulatorem P. Przyjęto parametr regulatora nieliniowego $k_{nl} = -30$. Wyraźnie widzimy, że im bliżej punktu pracy w chwili początkowej znajduje się układ regulacji, tym lepiej zmienna $\tilde{H}_3(t)$ przybliża przebieg zmiennej $\Delta H_3(t)$.

Rozważmy układ regulacji z regulatorem P dla wahadła. Opis nieliniowego układu regulacji składa się z nieliniowych równań stanu obiektu

$\begin{eqnarray} \dfrac{d\theta(t)}{dt} &=& \omega(t) \qquad(2.52) \\ \dfrac{d\omega(t)}{dt} &=& \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} M(t) \qquad(2.53) \end{eqnarray}$

oraz równania regulatora P dla punktu pracy określonego przez  $\theta_{0}$, $\omega_{0}$ oraz $M_{0}$

$\begin{equation} M(t) = k_p (\theta(t)-\theta_0) + M_0 \qquad(2.54) \end{equation}$

Jeżeli wprowadzimy równanie regulatora P do równań stanu obiektu, to otrzymamy równania stanu układu regulacji

$\begin{eqnarray} \dfrac{d\theta(t)}{dt} &=& \omega(t) \qquad(2.55) \\ \dfrac{d\omega(t)}{dt} &=& \dfrac{g}{l}sin\theta(t) - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} \left( k_p (\theta(t)-\theta_0) + M_0 \right) \qquad(2.56) \end{eqnarray}$

Opis zlinearyzowanego układu regulacji składa się ze zlinearyzowanych równań stanu obiektu

$\begin{eqnarray} \dfrac{d\tilde{\theta}}{dt} &=& \tilde{\omega} \qquad(2.57)\\ \dfrac{d\tilde{\omega}}{dt} &=& \dfrac{g}{l}cos\theta_0 \tilde{\theta} - \dfrac{D}{ml^2} \tilde{\omega} + \dfrac{1}{ml^2} \tilde{M} \qquad(2.58) \end{eqnarray}$

oraz zlinearyzowanego równania regulatora P. Zapiszmy równanie regulatora P w postaci przyrostowej

$\begin{equation} \Delta M(t) = k_p \Delta \theta(t) \end{equation}\qquad(2.59)$

Powyższe równanie jest liniowe, zatem możemy natychmiast zapisać równanie zlinearyzowanego regulatora P jako 

$\begin{equation} \tilde{M}(t) = k_p \tilde{\theta}(t) \end{equation}\qquad(2.60)$

Jeżeli wprowadzimy zlinearyzowane równanie regulatora P do zlinearyzowanych równań stanu obiektu, to otrzymamy zlinearyzowane równania stanu układu regulacji

$\begin{eqnarray} \dfrac{d\tilde{\theta}}{dt} &=& \tilde{\omega} \qquad(2.61)\\ \dfrac{d\tilde{\omega}}{dt} &=& \dfrac{g}{l}cos\theta_0 \tilde{\theta} - \dfrac{D}{ml^2} \tilde{\omega} + \dfrac{1}{ml^2} k_p \tilde{\theta}(t) = \left( \dfrac{g}{l}cos\theta_0 + \dfrac{1}{ml^2} k_p \right) \tilde{\theta} - \dfrac{D}{ml^2} \tilde{\omega} \qquad(2.62) \end{eqnarray}$

Powyższe równania stanu moglibyśmy także uzyskać poprzez bezpośrednią linearyzację równań stanu nieliniowego układu regulacji. Podobnie jak to było w przypadku linearyzacji równań obiektu, omówionych w poprzednim module, formułujemy następujący postulat.

Postulujemy, że jeżeli zachodzą następujące warunki 

• warunki początkowe dla zmiennych $\tilde{\theta}$, $\tilde{\omega}$ są dokładnie równe przyrostom zmiennych $\theta$ oraz $\omega$ w chwili początkowej

$\begin{eqnarray} \tilde{\theta}(t_0) &= &\Delta \theta(t_0) = \theta(t_0) - \theta_0 \qquad(2.63) \\ \tilde{\omega}(t_0) &= &\Delta \omega(t_0) = \omega(t_0) - \omega_0\qquad(2.64) \end{eqnarray}$

• w pewnym ustalonym przedziale czasu $t\in [ t_0, t_1 ]$ rozwiązania $\theta(t)$, $\omega(t)$ nieliniowych równań stanu układu regulacji (\ref{eq:ch2:rownanieStanuTheta001})-(\ref{eq:ch2:rownanieStanuOmega001}) pozostają w otoczeniu punktu pracy $(\theta_0, \omega_0)$ ($C_{\theta}, C_{\omega}$ -- stałe dodatnie)

$\begin{eqnarray} | \theta(t)-\theta_0 | &=& | \Delta \theta(t) | \leq C_{\theta} \qquad(2.65) \\ | \omega(t)-\omega_0 | &=& | \Delta \omega(t) | \leq C_{\omega} \qquad(2.66) \end{eqnarray}$

to rozwiązania $\tilde{\theta}(t)$ oraz $\tilde{\omega}(t)$ liniowych równań stanu układu regulacji 2.61)-(2.62) dobrze przybliżają przyrosty zmiennych stanu dla $t\in [ t_0, t_1 ]$ tzn. w tym przedziale czasu zachodzą przybliżone warunki

$\begin{eqnarray} \tilde{\theta}(t) &\simeq& \Delta \theta(t) \qquad(2.67)\\ \tilde{\omega}(t) &\simeq& \Delta \omega(t) \qquad(2.68) \end{eqnarray}$

Przybliżenie to jest tym lepsze im bliżej wybranego punktu pracy pozostają rozwiązania nieliniowych równań stanu tzn. im mniejsze są stałe $C_{\theta}, C_{\omega}$ w równaniach (2.65)-(2.66). 

Aby przetestować zdolność zlinearyzowanego modelu układu regulacji do przybliżania dynamiki układu nieliniowego porównajmy przebiegi czasowe zmiennych stanu dla obu modeli. Przyjmujemy parametry obiektu $m = 0.1$, $l = 1$, $g = 10$, $D = 0.1$. Wybieramy punkt pracy odpowiadający $\theta_0=\dfrac{\pi}{6}$, $\omega_0=0$ oraz $M_{0} = -0.5$. Przyjmujemy wzmocnienie regulatora równe $k_p = -1$. Taka wartość wzmocnienia zapewnia stabilizację układu regulacji do wybranego punktu pracy. Zmienne stanu obiektu zlinearyzowanego $\tilde{\theta}(t)$, oraz $\tilde{\omega}(t)$ przybliżają przyrosty zmiennych stanu obiektu nieliniowego $\Delta \theta$, $\Delta \omega$. Wykonamy symulacje dla czterech zestawów warunków początkowych. Warunki początkowe dla przyrostów zmiennych stanu wynoszą

• $\Delta \theta(t_0) = \dfrac{\pi}{3}$, $\Delta \omega(t_0) = -1$

• $\Delta \theta(t_0) = \dfrac{\pi}{6}$, $\Delta \omega(t_0) = -0.5$

• $\Delta \theta(t_0) = \dfrac{\pi}{15}$, $\Delta \omega(t_0) = -0.2$

• $\Delta \theta(t_0) = \dfrac{\pi}{30}$, $\Delta \omega(t_0) = -0.1$

a) $\Delta \theta(t_0) = \dfrac{\pi}{3}$, $\Delta \omega(t_0) = -1$

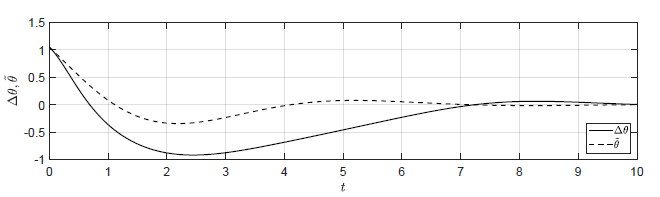
b) $\Delta \theta(t_0) = \dfrac{\pi}{6}$, $\Delta \omega(t_0) = -0.5$

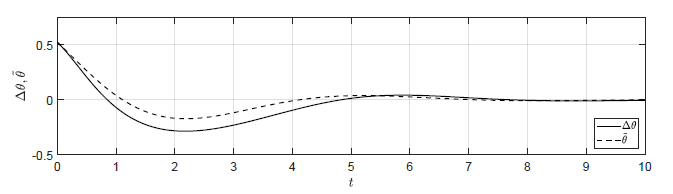
c) $\Delta \theta(t_0) = \dfrac{\pi}{15}$, $\Delta \omega(t_0) = -0.2$

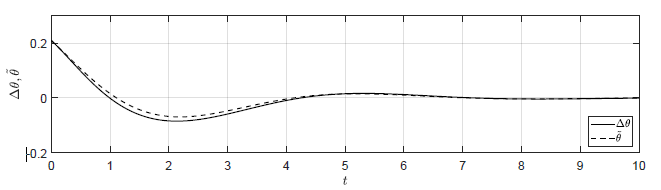
d) $\Delta \theta(t_0) = \dfrac{\pi}{30}$, $\Delta \omega(t_0) = -0.1$

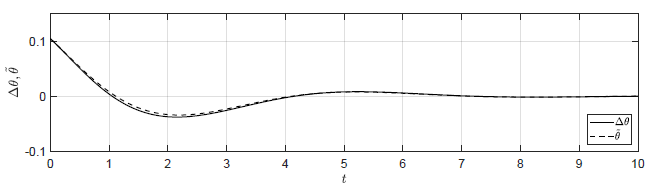
Rysunek 2.13 Porównanie trajektorii $\Delta \theta(t)$  nieliniowego układu regulacji oraz trajektorii $\tilde{\theta}(t)$ układu zlinearyzowanego w odpowiedzi na niezerowe warunki początkowe.

Warunki początkowe dla zmiennych przyrostowych zmniejszają się proporcjonalnie dla kolejnych zestawów. Spodziewamy się, że dla coraz mniejszych początkowych przyrostów, trajektorie zmiennych stanu obiektu zlinearyzowanego będą coraz lepiej przybliżać trajektorie przyrostów stanu obiektu nieliniowego. Zgodnie z (2.63)-(2.64) warunki początkowe dla modelu zlinearyzowanego wynoszą

$\begin{equation} \tilde{\theta}(t_0) = \Delta \theta(t_0),\ \tilde{\omega}(t_0) = \Delta \omega(t_0) \end{equation}\qquad(2.69)$

Na Rys. 2.13 przedstawiono porównanie trajektorii zmiennej przyrostowej $\Delta \theta(t)$  nieliniowego układu regulacji i zmiennej $\tilde{\theta}(t)$ układu zlinearyzowanego dla wybranych zestawów warunków początkowych. Wyraźnie widzimy, że im bliżej punktu pracy w chwili początkowej znajduje się układ regulacji, tym lepiej zmienna $\tilde{\theta}(t)$ przybliża przebieg zmiennej $\Delta \theta(t)$.