Podręcznik: Zadanie optymalnego planowania produkcji

2. Przykłady zadań optymalizacji

2.1. Zadanie optymalnego planowania produkcji

Wytwarzanie benzyn do silników spalinowych jest jednym z głównych procesów technologicznych rafinerii ropy naftowej. Przyjmijmy, że rafineria produkuje dwa rodzaje benzyny, które powstają w wyniku komponowania (zmieszania) różnych frakcji benzynowych oraz innych składników. Jeżeli z naszych rozważań wykluczymy, dla ułatwienia, procesy destylacji, rafinacji i reformingu, to uproszczony schemat przepływów związany z produkcją benzyn może być taki jak na poniższym rysunku.

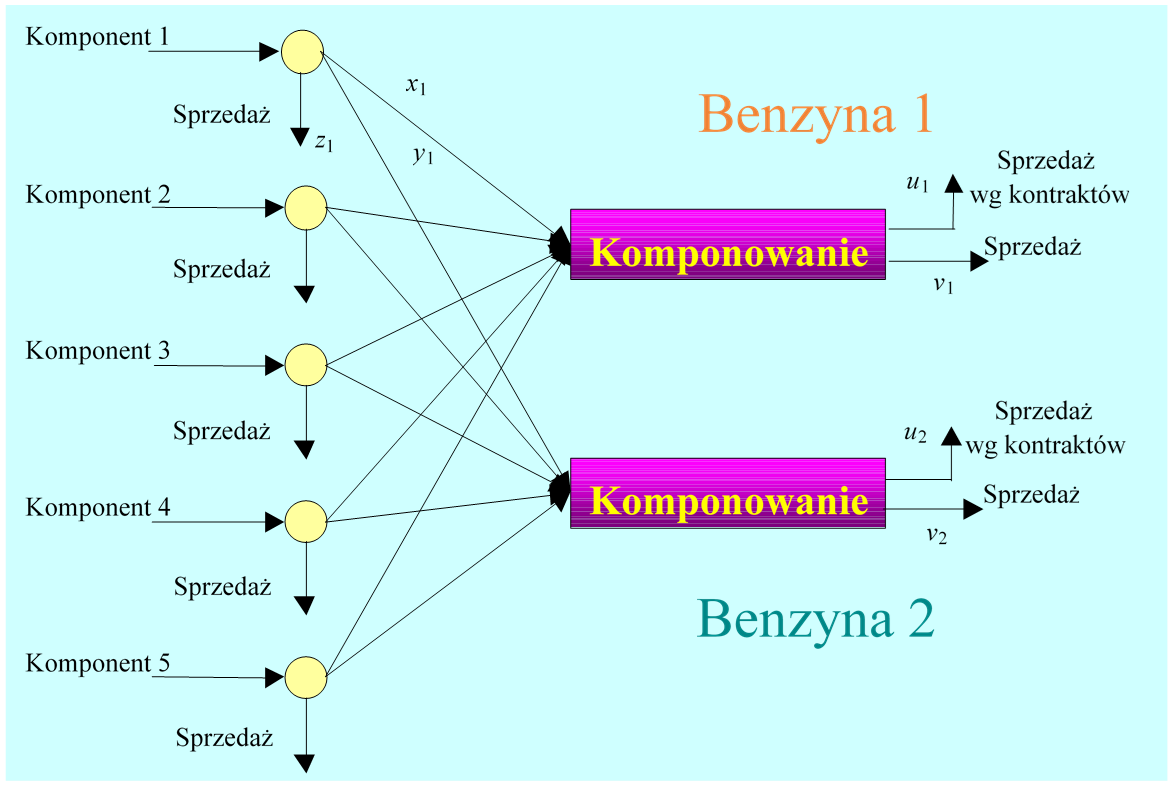
Rys. 1.1: Uproszczony schemat przepływów związany z produkcją benzyn

Dalej interesować nas będą tylko aspekty ekonomiczne związane z produkcją i sprzedażą benzyn w danym okresie, np. kwartale. Jeżeli znamy nakłady jednostkowe oraz jednostkowe ceny sprzedaży dla poszczególnych komponentów oraz ceny jednostkowe obu rodzajów benzyn to zadanie planowania produkcji może być sformułowane następująco:
Wybrać takie wielkości produkcji komponentów oraz produktów końcowych, które przyniosą maksymalny zysk.

Zapiszmy to zadanie dokładniej.

Oznaczmy zbiór numerów komponentów przez

${1,2,...,5}=\overline{1,5}$ ; niech

$i \in \overline{1,5}$ oznacza numer komponentu, a dla każdego komponentu:

xito ilość tego komponentu użyta do produkcji benzyny 1,

y_ito ilość tego komponentu użyta do produkcji benzyny 2,

z_ito ilość tego komponentu przeznaczona na sprzedaż.

Niech dalej

$u_j,j\in\overline{1,2}$ , oznacza ilość j-tej benzyny sprzedawanej na podstawie kontraktów długoterminowych, a

$v_j,j\in\overline{1,2}$ , oznacza ilość j-tej benzyny kierowanej do sprzedaży bieżącej.

Przy tych oznaczeniach (czysty) zysk rafinerii jest równy

$\sum_{j}\ p_j^uu_j+\sum_{j}\ p_j^vv_j+\sum_{i}\ p_i^zz_i-\sum_{i}{c_i^s\left(x_i+y_i+z_i\right)}-\sum_{i}{c_i^b\left(x_i+y_i\right)}= =f(u_1,u_2,v_1,v_2,x_1,...,x_5,y_1,...,y_5,z_1,...,z_5)\qquad(1.1)$ ,

gdzie:

$p_j^u$ , – cena jednostki j-tej benzyny w kontrakcie,

$p_j^v$ ,– cena jednostki j-tej benzyny w wolnej sprzedaży,

$p_i^z$ , – cena jednostki i-tego komponentu w wolnej sprzedaży,

$c_i^s$ ,– koszt wytworzenia jednostki komponentu i,

$c_i^b$ , – koszty komponowania przeliczone na jednostkę komponentu i.

Określiliśmy tym samym kryterium (funkcję oceny, wyboru) pozwalające porównywać różne zestawy rozważanych wielkości (warianty decyzji).

Czy zadanie sformułowane następująco:

znaleźć taki zestaw wielkości

$(u_1,u_2,v_1,v_2,x_1,...,x_5,y_1,...,y_5,z_1,...,z_5)$ dla którego zysk rafinerii jest największy jest poprawne?

Po chwili zastanowienia każdy odpowie – nie.

Po pierwsze, wszystkie wielkości nie mogą być ujemne.

Po drugie obowiązuje prawo zachowania masy i suma ilości komponentów nie może być większa niż suma ilości produktów, a przy założeniu braku strat, musi być dokładnie taka sama.

W konsekwencji w poprawnym sformułowaniu zadania muszą pojawić się dodatkowe wymagania wiążące zmienne. Trzeba określić ograniczenia.

Ustalenie pierwszej grupy ograniczeń jest oczywiste:

$u_j\geq0,v_j\geq0,x_i\geq0,y_i\geq0,z_i\geq0,j\in\overline{1,2,}i\in\overline{1,5}\qquad(1.2)$ ,

są to tzw. ograniczenie znaku;

do których trzeba dodać równania bilansowe

$\sum_{i}\ x_i=u_1+v_1 oraz \sum_{i}\ y_i=u_2+v_2.$

Jakie jeszcze mogą być ograniczenia?

Sumaryczna ilość komponentu i-tego jaka może być dostarczona w danym okresie nie może przekroczyć zdolności produkcyjnej

$\alpha _i$

$x_i+y_i+z_i\le\alpha_i, \qquad(1.3)$

Nierówności, określające łącznie z równaniami bilansowymi, jakość produktów kompozycji

$\sum_{i}\eta_ix_i\geq\mu_1(u_1+v_1) i \sum_{i}\eta_iy_i\geq\mu_2(u_2+v_2);$

ograniczenie na minimalną ilość benzyny sprzedawanej po cenach ustalonych w kontrakcie

$u_1 \geq U_1, \, u_2 \leq U_2. \qquad(1.4)$

Ograniczenia znaku, bilansowe, zdolności produkcyjnej, jakości oraz minimalnych ilości zawężają pole wyboru wariantów do tzw. zbioru dopuszczalnego.

Poprawnie sformułowane zadanie planowania produkcji jest zatem następującym

zadaniem optymalizacji (w tym przypadku maksymalizacji):

znaleźć taki zestaw wielkości decyzyjnych

$(u_1,u_2,v_1,v_2,x_1,...,x_5,y_1,...,y_5,z_1,...,z_5)$ ; dla którego zysk rafinerii określony funkcją f jest największy, co,

oznaczając

$\mathbf{x}=(u_1,u_2,v_1,v_2,x1,...,x5,y1,...,y5,z1,...,z5) ,$ zapiszemy

znaleźć

$\mathbf{x}^\mathbf{o}={arg\max}_{\ \mathbf{x}\in\mathbf{X}\ }f(\mathbf{x}),$

gdzie zbiór dopuszczalny X jest równy

$\begin{eqnarray}\mathbf{X}={x\in\ R^{19}|u_j\geq0,\ \ v_j\geq0,\ \ x_i\geq0,\ \ y_i\geq0,\ \ z_i\geq0,\ \ \sum_{i}\ x_i=u_1+v_1,\ \ \sum_{i}\ y_i=u_2+v_2,… \\ x_i+y_i+z_i\le\alpha_i,\ \ \sum_{i}\eta_ix_i\geq\mu_1\left(u_1+v_1\right),\ \ \sum_{i}\eta_iy_i\geq\mu_2\left(u_2+v_2\right),\ \ j\in\overline{1,2,}i\in\overline{1,5}, \ \ u_1 \geq U_1, \, u_2 \leq U_2 }\qquad(1.5) \end{eqnarray}$ .

Posumowaniem naszych rozważań będzie wyliczenie kroków, które doprowadziły nas do zbudowania (modelu) zadania optymalizacji.

Określenie/identyfikacja wielkości, których wartości możemy wybierać, czyli zmiennych decyzyjnych. Jest ich 19, pogrupowanych w pięciu zestawach: ilości dostępnych komponentów użytych do produkcji benzyny pierwszego rodzaju $\left(x_i\right)_{i\in\overline{1,5}}$ , drugiego rodzaju i przeznaczonych na sprzedaż $\left(z_i\right)_{i\in\overline{1,5}}$ (15 zmiennych), ilości benzyny pierwszego rodzaju sprzedawanej na podstawie kontraktów długoterminowych $u_1\$ oraz na wolnym rynku $v_1$ (2 zmienne), ilości benzyny drugiego rodzaju sprzedawanej na podstawie kontraktów długoterminowych $u_2$ oraz na wolnym rynku $v_2$ (2 zmienne).
Ustalenie kryterium wyboru, w tym przypadku funkcji rzeczywistej 19 zmiennych decyzyjnych. Wybrano zysk (1.1), co automatycznie, z jednej strony określiło zadanie optymalizacji jako maksymalizację, a z drugiej pociągnęło konieczność ustalenia/identyfikacji wartości dziewięciu cen (kontraktowej ceny jednostki pierwszej benzyny $\ {\ p}_{j1}^u$ i drugiej benzyny $p_2^u$ , wolnorynkowej ceny jednostki pierwszej benzyny $p_1^v$ i drugiej benzyny $p_2^v$ oraz ceny jednostki każdego komponentu w wolnej sprzedaży $p_i^z, i\in\overline{1,5}$ ) i dziesięciu kosztów ( $c_i^s$ – koszt wytworzenia jednostki komponentu $i, i\in\overline{1,5}, c_i^b$ – koszty komponowania przeliczone na jednostkę komponentu $i, i\in\overline{1,5},$ ) to jest 19 parametrów.
Ustalenia/identyfikacji dodatkowych wymagań wiążących zmienne decyzyjne to jest ograniczeń. Ograniczenia tworzą dwie grupy:

ograniczenia nierównościowe; są to prawie zawsze ograniczenia znaku (1.2), ograniczenia wynikające z zasad bezpieczeństwa oraz np. tak jak w rozpatrywanym przypadku nierówności gwarantujące niezbędną jakość wyrobów, czy minimalną produkcję (1.4) zmieniając stosowne ograniczenia znaku,
ograniczenia równościowe; najczęściej bilansowe, ale także ograniczenia wynikające z konstrukcji aparatów produkcyjnych limitujące wielkość produkcji/przetwarzania. Te ostatnie w naszym przykładzie zostały potraktowane jako ograniczenia nierównościowe, co oznacza, że modelujący zadanie optymalizacji dopuszcza niewykorzystanie wszystkich potencjalnie dostępnych zdolności produkcyjnych, nierówność (1.3).

Przykład drugi przedstawi zadanie inżyniera – zadanie optymalnego zaprojektowania pewnego wyrobu, w tym przypadku układu automatycznej regulacji.