Podręcznik
2. Przykłady zadań optymalizacji
2.2. Zadanie projektowania optymalnego regulatora PID
Przyjmijmy, że naszym zadaniem jest zaprojektowanie autopilota dla statku, tzn. takiego urządzenia, które wyręczy sternika w stałym utrzymywaniu ustalonego kursu. Nasze dalsze rozważania będziemy prowadzić przy upraszczającym założeniu, że znamy opis zależności między zmianami kąta wychylenia steru, \( \delta \), a zmianami kursu statku, \(\varphi\). Przyjmujemy, że jest to liniowe równanie różniczkowe
\(TT_{ms}\dddot{(\varphi}+(T+T_{ms})\ddot{<span>\varphi</span>}+\dot{<span>\varphi</span>}=k\delta\)
(tzw. model K. Nomoto pierwszego rzędu z maszyną sterową).
Automatycy przy projektowaniu układów sterowania zamiast „opisem różniczkowym” obiektu liniowego wolą posługiwać się równoważnym opisem transmitancyjnym przyjmując, że funkcja \(\varphi(\cdot)\) będąca rozwiązaniem równania różniczkowego obiektu oraz sygnał sterujący \(\delta(\cdot)\)mają transformaty Laplace’a
\(s\bar{<span>\varphi</span>}(s)=\mathcal{L}(\varphi(t)), s↦\bar{\delta}(s)=L(δ(t))\).
Dokonując transformacji Laplace’a obu stron powyższego równania różniczkowego można je zapisać jako równanie algebraiczne
\(TT_{ms}s^3 \bar{</span>\varphi</span>}(s)+(T+T_{ms})s^2\bar{</span>\varphi</span>}(s)+s\bar{</span>\varphi</span>}(s)=\bar{\delta}(s),\)
a następnie w postaci transmitancyjnej
\(\bar{\varphi }=\dfrac{k}{s(Ts+1)(T_{ms}s+1)}\bar{\delta}(s)=G(s)\bar{\delta}(s)\)
\(\bar{</span>\varphi</span>}(s)=G(s)\bar{\delta}(s)\).
Strukturę sytemu sterowania wybierzemy oczywiście jako zamkniętą, ponieważ tylko taki autopilot ma szansę poradzenia sobie z różnymi zakłóceniami oddziaływującymi na statek (zniwelowania ich wpływu na kurs statku). Sterowanie (kąt wychylenia steru) będzie zatem wyznaczane w oparciu o uchyb e, tzn. różnicę miedzy zadanym, \(φ_d \), a zmierzonym, \(φ_d \),, kursem statku.
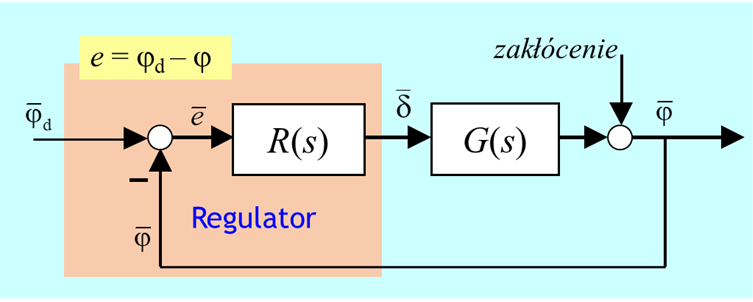
Trzeba wyznaczyć transmitancję regulatora \(\bar{\delta}(s)=R(s)\bar{</span></span></span></span></span>e}(s)\)
Wieloletnie doświadczenie, a także stosowne rozważania teoretyczne, podpowiadają w naszym przypadku wybór sposobu przetwarzania (sygnału) uchybu na sterowanie. Powinien to być tzw. algorytm regulatora PID, tj. algorytm opisywany transmitancją
\(R(s)=k_P(1+\dfrac{1}{T_Is}+T_Ds)\) (równaniem różniczkowym \(T_I\dot{\delta}=k_p(T_DT_I\ddot{e}+T_I\dot{e}+e)).\)
gdzie człon ostatni dokonuje różniczkowania uchybu (działanie D), a człon środkowy go całkuje (działanie I). „Jedynka”, łącznie z mnożnikiem \(k_P\) przetwarzają uchyb w sposób proporcjonalny (działanie P).
W transmitancji regulatora PID mamy trzy parametry – nastawy – \(k_P\), \(T_I\) oraz \(T_D\), których wartości trzeba tak wybrać aby zaprojektowany układ regulacji działał jak najlepiej.
Co znaczy przedstawione wymaganie: „działał jak najlepiej”?
Istnieje wiele odpowiedzi na to pytanie. Przedstawimy teraz krótko jedną z nich. Ponieważ znamy transmitancję statku I i transmitancję regulatora I, to możemy policzyć uchyb \(e_1(\cdot) \) w układzie regulacji dla zakłócenia będącego skokiem jednostkowym
\(\bar{e}_1(s)= \dfrac{G(s)}{1+G(s)R(s)}\dfrac{1}{s}\), \(e_1(t)=\mathcal{L}^{-1}(\bar{e}_1(s)).\)
W tej sytuacji „działał jak najlepiej” oznacza:
działał tak aby uchyb był bliski zera, tak jak tylko jest to możliwe. Jak tylko to jest możliwe, bo inżynier znający teorię regulacji wie, że np. wymaganie bezwzględnego zerowania się uchybu w każdej chwili jest nierealizowalne.
Jest oczywiste, że przebieg (kształt) uchybu zależy od nastaw regulatora:
\((\forall t \geq 0) e_1(t) = \Psi (t; k_P, T_I ,T_D )\).
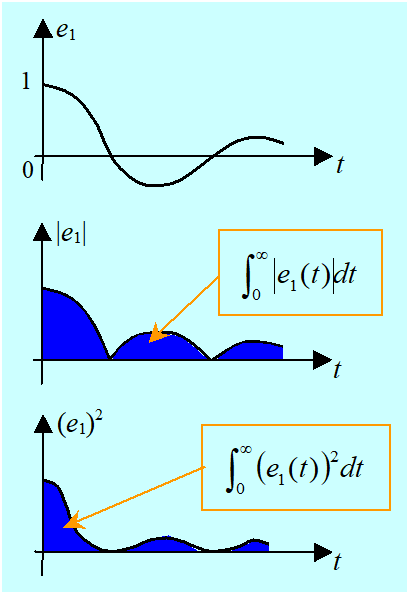
Zatem do oceny „odległości od zera” uchybu możemy posłużyć się całką z modułu uchybu:
\((k_P,T_I,T_D)\mapsto f^1(k_P,T_I,T_D)=\int_{0}^{\infty}\left|\psi(t;k_P,T_I,T_D)\right|\ dt,\)
albo całką z kwadratu uchybu:
\((k_P,T_I,T_D)\mapsto f^2(k_P,T_I,T_D)=\int_{0}^{\infty}{\left(\psi(t;k_P,T_I,T_D)\right)^2}dt.\)
Określiliśmy więc sposób porównywania różnych zestawów nastaw: ta trójka parametrów jest lepsza, dla której kryterium (wybrana funkcja oceny) przyjmuje mniejszą wartość.
W rozważanym zadaniu optymalizacji szukamy nastaw dających jak najbliższa zeru wartość funkcji oceniającej, zatem naszym zadaniem jest, w odróżnieniu od przykładu poprzedniego, minimalizacja.
Intuicyjnie jest dość oczywiste, że całka z modułu uchybu (kryterium \(f^1\)) jest lepszą miarą jakości działania układu regulacji niż całka z kwadratu uchybu (kryterium \(f^2)\), bo małe oscylacje uchybu nie wpływają wiele na tę ostatnią.
Dlaczego więc proponowane jest kryterium drugie?
W podręcznikach automatyki można znaleźć wzory pozwalające dla znanej transmitancji obiektu wyznaczyć analityczną zależność wartości tego kryterium od nastaw regulatorów. Innymi słowy możemy stosunkowo prosto wyznaczyć wzór pozwalający obliczyć wartości funkcji \((k_P,\ T_I,T_D) \mapsto f^2(k_P,\ T_I,T_D)=\ \int_{0}^{\infty}{\left(\psi(t;k_P,T_I,T_D)\right)^2}dt\). Natomiast dla danego zestawu nastaw \(\ (k_P,\ T_I,T_D)\), wartość funkcji \(f^1(k_P,\ T_I,T_D)\) możemy w zasadzie wyznaczyć tylko drogą rozwiązywania stosownego równania różniczkowego (symulacji) i numerycznego całkowania. Co oznacza, że przy tak określonym kryterium sprawdzimy tylko wybrane „trójki parametrów” bo całkujemy numerycznie. Wybór najlepszej z nich zależy więc silnie od naszej intuicji określającej jakie trójki wybierzemy do badania.
Bez względu na to jakie kryterium porównywania/oceny wybierzemy, musimy, tak jak poprzednio, odpowiedzieć na pytanie: czy nastawy kP, TI ,TD możemy wybierać dowolnie?
Oczywiście nie. Musimy pamiętać o tym, że algorytm regulatora PID będzie realizowany przez pewien układ fizyczny, dostępny na rynku, albo zaprojektowany przez nas, w którym wartości nastaw będą mogły się zmieniać tylko w określonych granicach:
\(0 < k_P^{min}\leq \ k_P\leq \ k_P^{max},\, 0 < T_I^{min}\ \leq T_I\leq \, T_I^{max},\, 0\leq \ T_D^{min}\ \leq T_D\ \leq T_D^{max}. \qquad (1.6)\)
Nie jest wykluczone, że ze względów konstrukcyjnych wystąpią wspólne ograniczenia np.:
\(g((T_I,T_D)\leq 0 \qquad (1.7)\)
gdzie \(\mathbb{R}^2((T_I,T_D) \mapsto g((T_I,T_D)\mathbb{R}\) jest znaną funkcją.
Podsumowując, zadanie projektowania autopilota dla statku, przy założeniu, że jako regulator wybieramy regulator PID, sprowadziliśmy do następującego
zadania minimalizacji (optymalizacji):
znaleźć takie wartości nastaw kP, TI ,TD w zbiorze określonym nierównościami (1.6) i (1.7) dla których funkcja oceny (kryterialna) \(f \, (f^1 \)albo \(f^2\)) przyjmuje najmniejszą wartość na tym zbiorze,
co będziemy zapisywać:
znaleźć \((k_P^o,T_I^o,T^o_D)= \mathrm{argmin}_{(k_P,T_I,T_D) ∈ X}f(k_P,T_I,T_D)\)
gdzie
\(X = {(k_P,T_I,T_D) | 0 < k_P^{min}\ leq k_P\ leq k_P^{max},\, 0 < T_I^{min}\leq T_I\ leq T_I^{max},\, 0\ leqT_D^{min}\ leq T_D\ leq T_D^{max}, g(T_I,T_D)\leq 0 } \qquad(1.8)\)
jest zbiorem dopuszczalnym.
Zwróćmy tu uwagę na, pozornie niewielką, różnicę w określeniu (1.8) zbioru dopuszczalnego w stosunku do przekładu poprzedniego. Wśród nierówności definiujących powyższy zbiór są ostre (<) i słabe (\(\leq\)), natomiast określenie zbioru dopuszczalnego (1.5) w poprzednim przykładzie zawierało tylko nierówności słabe. W konsekwencji zbiór (1.5) jest zbiorem domkniętym, a zbiór (1.8) może nie być zbiorem domkniętym. Jak się o tym przekonamy w punkcie 1.1 modułu trzeciego może to mieć przykrą konsekwencję w postaci nieistnienia rozwiązania zadania z nie domkniętym zbiorem dopuszczalnym.
Następny, krótki przykład związany jest z teorią identyfikacji i jest w zasadzie przykładem z dziedziny matematyki stosowanej.
