Podręcznik

Przypomnijmy zadanie, którym będziemy się dalej zajmować.

Zadanie optymalizacji bez ograniczeń (ZOBO):

znaleźć $x^o=\mathrm{argmin}_{x∈\mathbb{R}^n }⁡f (x)$

Zgodnie z przyjętym optymistycznym podejściem omawianym w rozdziale piątym zakładamy, że w ZOBO

• funkcja wyboru $f$ jest gładka, 
• potrafimy wyliczyć jej gradient $\bigtriangledown f$,
• gdy potrzebna – wyznaczyć macierz Hessego $\bigtriangledown ^2 f$.

Definicja kierunku poprawy d „wystawionego” w punkcie bieżącym $x{(k)},$ wymaga aby „ruch wzdłuż niego” dał zmalenie funkcji wyboru, co przy naszych założeniach zgodnie z Lematem 3.3, oznacza, że d jest kierunkiem poprawy gdy $∇f(x^{(k)})d$

Wobec tego narzucającym się kierunkiem poprawy jest kierunek antygradientu $d=-∇^T f(x^{(k)})$ (oczywiście w sytuacji gdy jest niezerowy) ponieważ 

$(∀x^{(k)}) ∇f(x^{(k)})(-∇^T f(x^{(k)}))=-‖∇f(x^{(k)})‖^2 < 0.$

Przy takim wyborze kierunku poprawy możemy podstawowy algorytm kierunków poprawy ukonkretnić do algorytmu realnego.

Algorytm gradientu (prostego) (Algorytm największego spadku, Algorytm Cauchy’ego)

Inicjalizacja

Ustal dokładność algorytmu $\varepsilon > 0$.

Wybierz punkt początkowy $x^{(0)}$, podstaw $x := x^{(0)}$,.

Podstaw $k := 0.$

Kroki algorytmu

1. Oblicz $∇f(x)$, podstaw $grad := ∇f(x)$.
2. Jako kierunek poprawy wybierz kierunek antygradientu podstawiając $d:=-(grad)^T$.
3. Wyznacz długość kroku $\alpha^{(k)}$ w kierunku antygradientu (kierunku poprawy) d, podstaw $α:=α^{(k)}$.
4. Wylicz następny punkt podstawiając $xnew:=x+α*d$.
5. Podstaw $k := k + 1$. Oblicz $∇f(xnew)$, oraz $||∇f (xnew)||$, podstaw $grad := ∇f(xnew)$, podstaw $norm := ||∇f(xnew)||$. Jeżeli $norm < \varepsilon$, to $xnew$ przyjmij za rozwiązanie, podstaw $ilosc_iteracji := k$  i stop. W przeciwnym przypadku podstaw $x := xnew$ i idź do 2

Nie sprecyzowaliśmy jak w kroku 2. algorytmu ustalić długość kroku w kierunku antygradientu. Trzeba zrobić to tak aby można było pokazać, że generowany przez algorytm ciąg punktów $\left\{ x^{(k)}\left. \right \}\right. _{k=0}^∞$ jest w określonym sensie zbieżny. Rozwiązanie tego zagadnienia daje następujące twierdzenie.

Zatem przy stosunkowo słabych założeniach mamy relatywnie słabą zbieżność algorytmu największego spadku – zbieżność nieskończoną do punktu stacjonarnego gradientu.

Przy odpowiednio mocniejszych założeniach o funkcji wyboru można pokazać, że algorytm ten zbiega liniowo do punktu minimalizującego. 

Wiemy już, że teoretycznie, algorytm gradientu prostego może znaleźć rozwiązanie zadania minimalizacji. Zbadajmy jego zachowanie rozwiązując proste zadanie minimalizacji.

PRZYKŁAD 4.1 
Rezultaty działania algorytmów optymalizacji można przedstawiać na dwa sposoby: za pomocą tabelek, lub rysunków. Jeżeli funkcja celu ma więcej niż trzy argumenty, to wymyślenie dobrego rysunku ilustrującego zachowanie się algorytmu może być trudne i pozostają tylko tabelki. Natomiast dla funkcji dwu-argumentowych stosowne rysunki pokazujące kolejne kroki (trajektorię) algorytmu na płaszczyźnie na tle wykresu poziomicowego funkcji minimalizowanej niosą w sobie najpełniejszą, intuicyjnie zrozumiałą informację o zachowaniu się algorytmu. Trzeba tylko dobrze dobrać funkcję celu – dostatecznie trudną dla algorytmów lecz o stosunkowo łatwych do narysowania poziomicach.
Rysunek prezentowany w tym przykładzie przedstawia poszczególne punkty znalezione przez algorytm największego spadku z metodą interpolacji kwadratowej użytą do minimalizacji w kierunku, który miał znaleźć rozwiązanie zadania minimalizacji funkcji dwu zmiennych

$(x_1,x_2)↦f(x_1,x_2)=(x_1-2)^4+(x_1-2x_2 )^2$

z dokładnością $\varepsilon = 0.1$ i wystartował z punktu $x^{(0)}=(0,3)$. Rozwiązaniem dokładnym zadania jest $x^o = (2,1)$.

  

Rys. 4.8: Trajektoria algorytmu prostego gradientu

Algorytm wykonał osiem kroków i zatrzymał się w punkcie $x^(8) = (2.27,1.12)$ w którym $‖∇f(2.27,1.12)‖=0.09$. Wartość funkcji celu $f (2.27,1.12) = 0.0062$, a odległość proponowanego rozwiązania od punktu optymalnego jest równa

$‖x^{(8)}-x^o ‖=0.3$.

Zwróćmy uwagę, że chcieliśmy rozwiązać zadanie minimalizacji tak jak było ono sformułowane w punkcie 3.1.1  Modułu trzeciego (ZOBO) tzn.

znaleźć $x^o=⁡\mathrm{argmin}_x  [(x_1-2)^4+(x_1-2x_2 )^2]$,

a właściwie znaleźliśmy rozwiązanie zadania

znaleźć $f^o= \mathrm{min}_x [(x_1-2)^4+(x_1-2x_2 )^2]$,

Można pomyśleć, że przyczyną takiego zachowania się algorytmu jest kryterium stopu zatrzymujące algorytm gdy gradient jest niewielki, a więc kryterium oparte na wartościach funkcji a nie jej argumentach. Wobec tego zamiana go np. na wymaganie

$\dfrac{‖x^((k))-x^((k-1)) ‖}{‖x^((k-1)) ‖}$

oceniające relatywny przyrost kroku, powinna poprawić wynik. Policzmy jednak ten iloraz dla ósmego kroku

$\dfrac{‖x^{(8)}-x^{(7)} ‖}{‖x^{(7)} ‖} =\dfrac{‖(2.27,1.12)-(2.28,1.15)‖}{‖(2.28,1.15)‖} =\dfrac{0.0316}{2.5536} =0.0124$.

Jest więc jeszcze mniejszy niż norma gradientu.
I nie jest to przypadek. Zatrzymanie algorytmu relatywnie daleko od punktu minimalizującego wynika z właściwości funkcji, która w sporym otoczeniu minimum zmienia się niewiele (wartość poziomicy w punkcie $x^{(3)}$ wynosi 0.09!). Takie zachowanie funkcji ścisłe wypukłych nie jest rzadkością – po prostu, wiele funkcji ściśle wypukłych w zbyt dużym otoczeniu swojego minimum, z praktycznego punktu widzenia, traci swoją ścisłą wypukłość stając się funkcjami „prawie stałymi”, w naszym przypadku o wartości niewiele różnej od zera. W konsekwencji zależności przyjęte w określeniu kryterium stopu szybko stają się niewielkie, co prowadzi do zbyt wczesnego (z punktu widzenia dokładności znalezienia punktu minimalizującego) zatrzymania algorytmu. 
Jeżeli zatem zależy nam na dokładnym wyznaczeniu punktu minimalizującego funkcję celu, której zachowania w okolicy minimum nie znamy (a tak jest przecież najczęściej), to musimy w kryterium stopu wybrać bardzo wysoką dokładność, tzn. bardzo małe $\varepsilon$, rzędu 10–4 lub mniejsze. Ceną jaką możemy za takie wymaganie zapłacić może być bardzo wiele kroków algorytmu, a więc długi czas obliczeń.
Jaki rysunek dostajemy dla zwiększonej dokładności?

 

Rys. 4.9: Trajektoria algorytmu prostego gradientu dla wysokiej dokładności

Po „dużym skoku” z punktu początkowego (w typ przypadku wynikającego z wyboru punktu startowego), generowane kierunki są coraz bardziej prostopadłe do drogi która prowadzi do minimum a kroki coraz krótsze i ruch algorytmu ma charakter zygzaka o coraz mniejszych wahaniach.

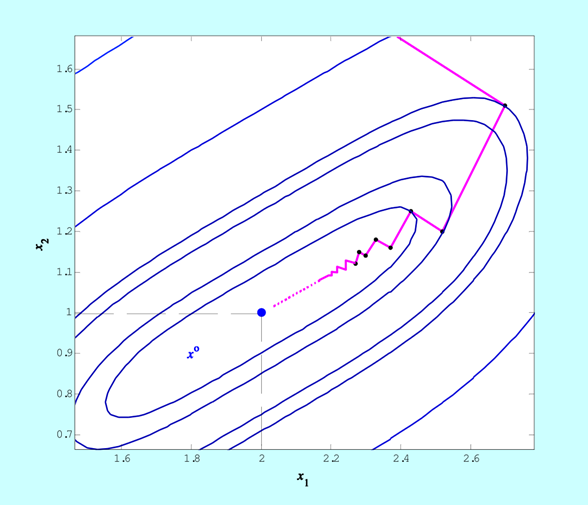
Przedstawione w przykładzie zachowanie – zygzakowanie – omawianego algorytmu, szczególnie wyraźne gdy napotka na długą i powoli opadającą „dolinę”, oznacza bardzo powolne zbliżanie się do rozwiązania i stanowi podstawową wadę algorytmu największego spadku. Kłopoty w takiej sytuacji są powiększane jeszcze tym, że składowe gradientu są coraz mniejszymi liczbami, a więc ich wyznaczenie jest obarczone coraz większym błędem względnym, co oznacza, że ruch w kierunku punktu minimalizującego jest nie tylko powolny ale i coraz bardziej niepewny.

Funkcja rozpatrywana powyżej była mniej złośliwa niż bananowa funkcja Rosenbrocka, której poziomice rysowaliśmy w poprzednich modułach. Jak poradzi sobie algorytm gradientu prostego ze znalezieniem minimum funkcji o której wiemy, że spełnia nasze optymistyczne założenia tylko w niewielkich otoczeniach punktu bieżącego?

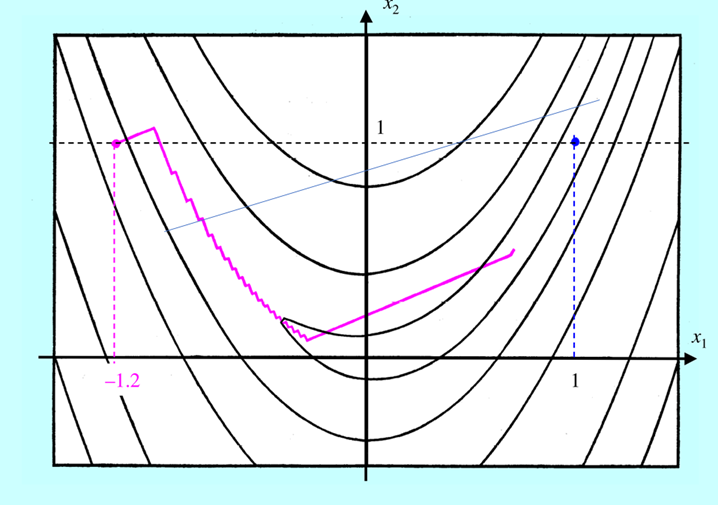
Jak widać nie najlepiej. Algorytm szybko zaczął „zygzakować”, potem odważnie „wyskoczył” z doliny prowadzącej do minimum, lecz po powrocie na jej dno zaczął zmierzać do celu tak drobnymi zygzakami, że przez pozostałe 960 iteracji posunął się bardzo niewiele. „Odwaga” była tu jednak przypadkowa. Od mniej więcej szóstej iteracji algorytm generuje kierunek poprawy (zaznaczony linią) na którym funkcja minimalizowana w kierunku f P ma dwa minima lokalne: „bliższe”, położone koło punktu startowego i „dalsze’, położone z drugiej strony góry które jest globalne. Do trzydziestej szóstej iteracji, zastosowana metoda interpolacji kwadratowej znajdowała pierwsze minimum (przypomnijmy sobie rysunek 4.2) i dopiero w trzydziestej ósmej – „przeskoczyła” to lokalne minimum i znalazła odległe minimum globalne. W tym przykładzie widać, że dokładna minimalizacja w kierunku może istotnie zmniejszyć ilość iteracji algorytmu największego spadku, ale nie wyeliminuje „zygzakowania”.

Obie omawiane funkcje spełniają założenia, nawet tych silniejszych twierdzeń o zbieżności. Przedstawione przykłady pokazują więc, że zbieżność teoretyczna to jedno, a 

Badanie zbieżności teoretycznej jest bardzo ważne przy konstruowaniu algorytmów. Trzeba przecież sprawdzić czy algorytm, który wymyśliliśmy ma w ogóle szansę na „dobiegnięcie” do rozwiązania. Teoria pozwala odrzucić pomysły bez sensu. Niestety bardzo rzadko rozważania teoretyczne pozwalają wyeliminować od razu pomysły, które w praktycznej realizacji są nieudane. Wynika to z faktu, że narzędzia (system pojęć składających się na modele analizy matematycznej) nie są dostosowane do potrzeb analizy zachowania algorytmów czyli tzw. analizy numerycznej.

Rożne próby zastosowania metody największego spadku pokazały już dawno, że metoda ta w rozsądnym czasie może dać rozwiązanie tylko dla najprostszych, dobrze uwarunkowanych w całej przestrzeni zadań. Zatem, gdy chcemy mieć skuteczniejsze narzędzia musimy albo metodę gradientu zmodyfikować, albo (w ramach metod kierunków poprawy) wymyślić zupełnie inne podejście.

Z wielu pomysłów, które pojawiły się w ostatnich sześćdziesięciu paru latach próbę praktycznej przydatności przetrwały w zasadzie tylko dwa algorytmy. Zanim je przedstawimy, przez chwilę zastanowimy się, dlaczego algorytm gradientu prostego działa tak źle.

Posłużenie się regułami zapisanymi w dowolnym algorytmie przeznaczonym do znalezienia rozwiązania zadania optymalizacji (algorytmie optymalizacji) daje ciąg punktów zaczynający się od punktu startowego (z numerem 0), którego wyznaczanie można opisać następującym wzorem

$x^{(k+1)}=\mathfrak{A} (x^{(k)},...),\, x^{(0)}\,\, \mathrm{ dane .} \qquad (4.1)$

W operatorze $\mathfrak{A}$ nie wpisaliśmy wszystkich argumentów, ponieważ sposób generacji nowego punktu musi zależeć od punktu bieżącego i może zależeć od punktów poprzednich, od historii. Innymi słowy algorytm może być bez pamięci i z pamięcią. Wypisując wzór, tej drugiej możliwości nie chcieliśmy wykluczyć, a także nie chcieliśmy określić tzw. głębokości pamięci, to znaczy określić ile kroków wstecz jeszcze uwzględniamy. Dla matematyka wzór (4.1) to równanie różnicowe, „bliski krewny” równań różniczkowych zwyczajnych rozważanych w pierwszym wykładzie. Badanie zbieżności algorytmów optymalizacji, to nic innego jak badanie asymptotycznych własności rozwiązań (szczególnych) takich równań różnicowych.

Jeżeli w ten sposób analizować zachowanie algorytmu gradientu prostego, to mamy

$x^{(k+1)}=x^{(k)}-α^{(k)} ∇^T f(x^{(k)})=\mathfrak{A} (x^{(k)})$,

i łatwo jest zauważyć, że główną przyczyną zygzakowania jest brak pamięci – nowy kierunek w żaden sposób nie jest związany z poprzednim, a intuicyjnie jest oczywiste, że wprowadzenie takiego związku uspokoiłoby zbyt nerwowe ruchy algorytmu. Nie może jednak „przedawkować ze środkiem uspokajającym”, bo i tak, jak widzieliśmy, po pewnym czasie zygzaki stają się zygzaczkami i algorytm prawie że stoi w miejscu. Można jednak zapisać dwa warianty modyfikacji mogące dać poprawę zachowania: 

• prostszy, polegający na dodaniu „poprawki” zależnej od „historii”: 

$x^{(k+1)}=x^{(k)}-α^{(k)} (∇^T f(x^{(k)})+p(x^{(k)},x^{(k-1)},...))=\mathfrak{A} (x^{(k)},x^{(k-1)},...)$,

• i mniej oczywisty – przeskalowujący gradient, też w zależności od „historii”:

$x^{(k+1)}=x^{(k)}-α^{(k)} \mathfrak{D}(x^{(k)},x^{(k-1)},...)∇^T f(x^{(k)})=\mathfrak{A} (x^{(k)},x^{(k-1)},...)$.

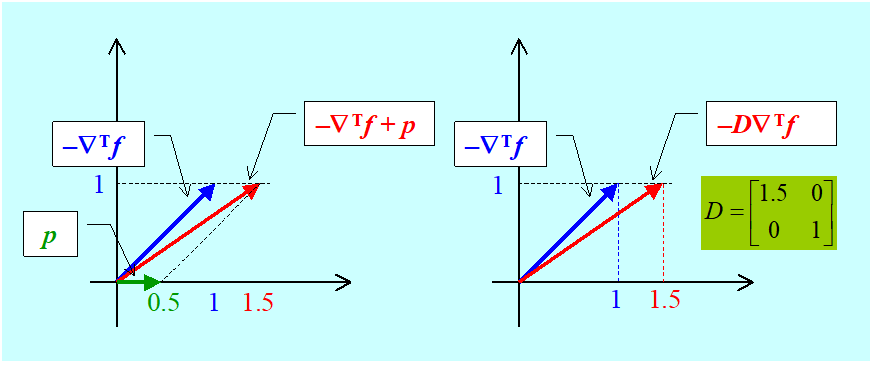
Jak zatem określać poprawkę addytywną $p(\cdot )$ albo, w najprostszym przypadku, kwadratową macierz transformacji $D(\cdot ) = \mathfrak{D}(\cdot )$ ?

Odpowiemy na to pytanie w dwu kolejnych punktach.