Podręcznik

Zajmiemy się najpierw przypadkiem pierwszym – poprawką addytywną.

Przyjmijmy na moment, że chcemy minimalizować metodą gradientu prostego funkcję kwadratową o dodatnio określonej macierzy Q:

Rysunek zrobimy dla funkcji dwu zmiennych.

Algorytm wystartował z punktu $x^{(0)}$ i w kierunku antygradientu $d^{(0)}=-∇^T f(x^{(0)})$ dokładnie minimalizując w kierunku znalazł punkt $x^{(1)}=x^{(0)}-α^{(0)} ∇^T f(x^{(0)})$. Następny krok zaprowadzi go do punktu $x^{(2)}$ leżącego na prostej wyznaczonej przez antygradient $-∇^T f(x^{(1)})=d^{(1)}$, i tak dalej. Zauważmy, że tak wyznaczane kolejne kierunki poprawy (antygradienty) są do siebie prostopadłe 

$∇f(x^{(k)})∇^T f(x^{(k+1)})=0,\,  k=0,1,\qquad (4.2)$

nie tylko dla funkcji kwadratowych, ale dla dowolnych funkcji różniczkowalnych, ponieważ kolejne punkty $x^{(k+1)}=x^{(k)}-α^{(k)} ∇^T f(x^{(k)})$ są punktami minimalizującymi funkcję

$α↦f_P (α;x^{(k)},-∇^T f(x^{(k)}))=f(x^{(k)}-α∇^T f(x^{(k)}))$,

co oznacza, że spełniony jest warunek (różniczkowanie funkcji złożonej)

Rysunek pokazuje, że w punkcie $x^{(1)}$ istnieje kierunek lepszy od antygradientu, oznaczmy go q, mający tą własność, że dokładna minimalizacja na tym kierunku doprowadzi do rozwiązania $x^o$. Wyznaczyć ten kierunek jest łatwo. Przy naszych założeniach rozwiązanie zadania optymalizacji musi spełniać równanie (Twierdzenie 3.6):

$0=∇^T f(x^o)=2Qx^o+c$, co daje $x^o=-\dfrac{1}{2}Q^{(-1)} c$.

Zatem $q=x^o-x^{(1)}=-\dfrac{1}{2}Q^{(-1) }c-x^{(1)}$. Jak na razie, te obliczenia nic ciekawego nie dają, ale policzmy czemu równa się iloczyn $d ^{(0)}Qq = –\bigtriangledown f (x^{(0)} )Qq$. Najpierw zauważmy, że

$∇^T f(x^{(1)})=2Qx^{(1)}+c$ i jak pamiętamy $∇f(x^{(0)})∇^T f(x^{(1)})=0$.

Teraz możemy policzyć wartość interesującego nas iloczynu

$-∇f(x^{(0)})Qq=-∇f(x^{(0)})Q(-\dfrac{1}{2}Q^(-1) c-x^{(1)})=∇f(x^{(0)})(1/2 c+Qx^{(1)})=$

      $=∇f(x^{(0)})(\dfrac{1}{2} ∇^T f(x^{(1)}))=0$.

czyli

$-∇f(x^{(0)})Qq=0.\qquad  (4.3)$

Wprowadźmy następujące definicje:

Prawdzie jest następujące stwierdzenie

Najprostszym przykładem dwu wektorów sprzężonych są wektory prostopadłe, które są sprzężone względem macierzy jednostkowej. Trzy wektory w przestrzeni trójwymiarowej są sprzężone względem macierzy jednostkowej jeżeli każdy z nich jest prostopadły do płaszczyzny wyznaczonej przez dwa pozostałe. Zatem już w przestrzeni trójwymiarowej sprzężenie względem macierzy jednostkowej to inna własność niż prostopadłość.

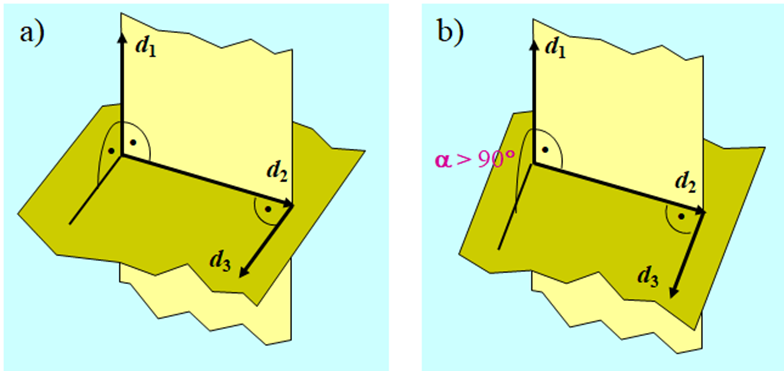
Wzór (4.3): $-∇f(x^{(0)})Qq=0$, pokazuje, że wektor antygradientu obliczony w punkcie początkowym $-∇^T f(x^{(0)})$ i wektor $q$ ustalający kierunek na którym leży punkt minimalizujący są sprzężone względem macierzy $Q$ określającej minimalizowaną funkcję kwadratową. 

Wektor $q$ jest dany wzorem $q=-\dfrac{}{2} Q^{-1} c-x^{(1)}$, zatem aby go obliczyć trzeba odwrócić macierz $Q$. 

Zastanowimy się teraz nad odpowiedzią na pytanie: czy można go wyznaczyć bez odwracania macierzy? 

Przyjmiemy zatem, że

$q=-∇^T f(x^{(1)})-β∇^T f(x^{(0)}), \qquad (4.4)$

gdzie współczynnik $\beta$ trzeba wyznaczyć. Do jego wyliczenia posłużmy się warunkiem Q-sprzężoności wektorów $-∇^T f(x^{(0)})$ i $q$  czyli równaniem  $-∇f(x^{(0)})Qq=0$. Zauważmy najpierw, że 

$x^{(1)}=x^{(0)}-α^{(0)} ∇^T f(x^{(0)})$,  czyli  $-∇f(x^{(0)})=\dfrac{1}{α^{(0)} }(x^{(1)}-x^{(0)} )^T$,

a także

$∇f(x^{(1)})-∇f(x^{(0)})=2(x^{(1)} )^T Q+c^T-2(x^{(0)} )^T Q-c^T=2(x^{(1)}-x^{(0)} )^T Q$.

Mamy zatem

$0=-∇f(x^{(0)} )Qq=-∇f(x^{(0)} )Q(∇^T f(x^{(1)} )+β∇^T f(x^{(0)} ))=$

$=\dfrac{1}{2α^ {(0)} }(∇f(x^ {(1)})-∇f(x^ {(0)}))(∇^T f(x^ {(1)})+β∇^T f(x^ {(0)}))$

co daje

$∇f(x^ {(1)})∇^T f(x^ {(1)})+ \underset{=0}{\underbrace{β∇f(x^ {(1)})∇^T f(x^ {(0)})}}-\underset{=0}{\underbrace{∇f(x^ {(1)})∇^T f(x^ {(0)})}}-β∇f(x^ {(0)})∇^T f(x^ {(0)})=0,$

Czyli

$β =\dfrac{∇f(x^{(1)} ) ∇^T f(x^{(1)} )}{∇f(x^{(0)} ) ∇^T f(x^{(0)} ) }. \qquad(4.5)$

Wzory (4.4) i (4.5) pozwalają więc wyznaczyć dla zadania optymalizacji o kwadratowej funkcji celu z macierzą Q, posługując się tylko gradientami, kierunek sprzężony względem Q z początkowym kierunkiem antygradientu.

Dla dwuwymiarowego przykładu tak określony kierunek „zaprowadzi” do rozwiązania (jest wektorem q). Jednak w przypadku wielowymiarowym tak być nie musi, bo wektorów sprzężonych do antygradientu jest nieskończenie wiele (jak wiemy, już w przestrzeni trójwymiarowej, jest nieskończenie wiele wektorów prostopadłych do danego wektora – leżą one na płaszczyźnie prostopadłej do tego wektora) a tylko jeden „prowadzi” do punktu minimalizującego. Nie znaleziono metody pozwalającej od razu wybrać ten właściwy wektor, udowodniono natomiast twierdzenie następujące.

Teza b) powyższego twierdzenia stwierdza więc, że za pomocą opisanego algorytmu można znaleźć rozwiązanie zadania minimalizacji funkcji kwadratowej w co najwyżej n krokach, inaczej mówiąc – dla funkcji kwadratowej algorytm ma skończoną zbieżność (pod warunkiem, że minimalizacja w kierunku jest dokładna, wzór (4.6)). Napisaliśmy „w co najwyżej...”, ponieważ teza a) twierdzenia mówi o tym, że kolejne kierunki są sprzężone z pierwszym – wektorem antygradientu, zatem zgodnie z naszymi wcześniejszymi rozważaniami kierunek prowadzący do minimum może zostać wyznaczony szybciej niż dopiero w n-tym kroku. Zauważmy też, że wzór (4.8) określający współczynnik ustalający „wkład” poprzedniego kierunku do nowego kierunku poprawy jest uogólnieniem wyprowadzonego poprzednio wzoru (4.5).

W twierdzeniu 4.2 został sformułowany algorytm o skończonej zbieżności pozwalający znaleźć rozwiązanie zadania minimalizacji ściśle wypukłej funkcji kwadratowej. Około 1963 R. Fletcher i C.M. Reeves zastosowali ten algorytm do minimalizacji funkcji wypukłej. Byli niepoprawnymi optymistami, bo z dowodu twierdzenia wynika, że skończona zbieżność algorytmu jest konsekwencją tego, że kolejne kierunki powiększają zbiór wektorów Q-sprzężonych, a przecież dla nie kwadratowej funkcji wypukłej nie można mówić o kierunkach sprzężonych względem macierzy Q, bo nie ma macierzy Q! Co więcej ta „kolejna sprzężoność” może nie być zachowana  nawet dla funkcji kwadratowej  gdy  minimalizacja  w  kierunku  nie  jest  dokładna.  Ale udało się – algorytm zachowywał się nadspodziewanie dobrze, potrafił na przykład bez zygzakowania, w rozsądnej liczbie kroków przy interpolacyjnej metodzie minimalizacji w kierunku znaleźć rozwiązanie dla bananowej funkcji Rosenbrocka. W artykule opublikowanym w 1964 r. Fletcher i Reeves nazwali swój algorytm Conjugate Gradient Method – metoda gradientu sprzężonego, i tak zostało, pomimo tego że kierunki generowane przez ich algorytm, choć oparte o gradient (patrz wzór (4.7)) dla funkcji nie kwadratowych nie są sprzężone. Intensywne badania metody gradientu sprzężonego prowadzone w drugiej połowie lat sześćdziesiątych doprowadziły do opublikowania w 1969 r. następującego algorytmu, w którym współczynnik $\beta^{(k)}$ jest wyliczany według innej zależności, zwanej wzorem Poljaka, Polaka, Ribière’a

$β^ {(k)}=\dfrac{∇f(x^ {(k)})(∇^T f(x^ {(k)})-∇^T f(x^ {(k-1)}))}{∇f(x^ {(k-1)})∇^T f(x^ {(k-1)})}.$

Algorytm gradientu sprzężonego (wersja Poljaka, Polaka, Ribière’a z odnową) 

Inicjalizacja

Ustal dokładność algorytmu $\varepsilon > 0.$

Wybierz punkt początkowy $x^{(0)}$, podstaw $x := x^{(0)}$.

Podstaw $k := 0$.

Kroki algorytmu

1. (Odnowa) Oblicz $∇f(x)$, podstaw $grad := ∇f(x)$, jako kierunek poprawy wybierz kierunek antygradientu podstawiając $d:=-(grad)^T$. Podstaw $l := 0$, idź do 4.
2. Podstaw   $β:=\dfrac{gradnew*((gradnew)^T-(grad)^T)}{grad*(grad)^T }$,    (stosujemy wzór Poljaka, Polaka, Ribière’a (4.9)).  Jako kandydata na kierunek poprawy wybierz wektor $dnew$, podstawiając   $dnew:=-(gradnew)^T+β*d$ (wzór (4.7)).
3. Jeżeli $gradnew*dnew$ ($dnew$ jest kierunkiem poprawy), podstaw $x := xnew, d := dnew$ oraz $grad:=gradnew$i przejdź do 4. W przeciwnym przypadku podstaw $x := xnew$ i przejdź do 1 (dokonaj odnowy).
4. Wyznacz długość kroku $\alpha^{(k)}$ w kierunku poprawy $d,$ podstaw$α:=α^ {(k)}$.
5. Wylicz następny punkt podstawiając $xnew:=x+α*d$.
6. Oblicz $∇f (xnew)$, oraz $||∇f (xnew)||$, podstaw $gradnew := ∇f (xnew)$, podstaw $norm := ||∇f (xnew)||$. 
7. Jeżeli $norm < \varepsilon$, to $xnew$ przyjmij za rozwiązanie, podstaw $ilosc_iteracji := k + 1$ i stop.
8. W przeciwnym przypadku idź do 7.
9. Podstaw $k := k + 1,$ podstaw $l := l + 1.$ Jeżeli $l < n$, gdzie$n$ jest wymiarem przestrzeni poszukiwań, to idź do 2. W przeciwnym przypadku podstaw $x := xnew$ i idź do 1 (odnowa po $n$ krokach od ostatniej odnowy).

Przeanalizujmy istotne aspekty działania przedstawionego wyżej algorytmu gradientu sprzężonego.

Jeżeli w kroku 4 algorytmu wykonamy dokładną minimalizację w kierunku, to kierunki wyznaczone w kroku 2 będą kierunkami poprawy, co poniżej pokażemy. 

Jak pamiętamy, przy naszych założeniach, kierunek $d^{(k)}$ jest kierunkiem poprawy gdy $∇f(x^ {(k)})d^ {(k)}$. Policzmy zatem ten iloczyn

$∇f(x^ {(k)})d^ {(k)}=∇f(x^ {(k)})(-∇^T f(x^ {(k)})+β^ {(k)} d^ {(k-1)})=-‖∇f(x^ {(k)})‖^2+β^ {(k)} ∇f(x^ {(k)})d^ {(k-1)}. (4.10)$

Pokażemy, że $∇f(x^ {(k)})d^ {(k-1)}=0$. Przy dokładnej minimalizacji w kierunku, dla punktu $x(k)$ zachodzą równości

$x^ {(k)}=x^ {(k-1)}+α^ {(k-1)} d^ {(k-1)}$

$α^ {(k-1)}=\mathrm{argmin}_{α≥0}f (x^ {(k-1)}-αd^ {(k-1)}),$

co oznacza, że spełniony jest warunek

$0=\dfrac{d}{dα} f(x^{(k-1) }-α^{(k-1) } d^{(k-1) }))=∇f(x^{(k-1) }-α^{(k-1) )}d^{(k-1)})(-d^{(k-1)})=-∇f(x^{(k)})d^{(k-1) }.$

Zatem z równości (4.10) wynika, że  $∇f(x^ {(k)})d^ {(k)}$

Oznacza to, że przy dokładnej minimalizacji w kierunku krok 3, sprawdzający czy kierunki wyznaczone w kroku 2 są kierunkami poprawy, nie jest potrzebny.

Wiemy jednak, że każda praktyczna realizacja minimalizacji w kierunku jest obarczona pewnym błędem. Zatem konstruując algorytm, który ma naprawdę służyć do rozwiązywania zadań optymalizacji musimy pamiętać o stosownych zabezpieczeniach pozwalających pokonać trudności związane z różnego rodzaju niedokładnościami obliczeniowymi. Warunek kroku 3 sprawdza czy wyliczony kierunek jest kierunkiem poprawy. Jeżeli nie jest, dokonuje się tak zwanej odnowy – jako kierunek poszukiwań wybierany jest antygradient, który (gdy nie jest zerowy) jest zawsze kierunkiem poprawy. Jeżeli jednak zbyt często będziemy zmuszeni stosować odnowę, to działanie algorytmu będzie niewiele różnić się od działania algorytmu największego spadku – w szczególności wystąpi „zygzakowanie”. Dlatego przy implementacjach metody gradientu sprzężonego do znajdowania długości kroku w kierunku najczęściej wybiera się jedną z metod dających dobrą aproksymację minimum w kierunku.

• Analizując zachowanie algorytmu największego spadku (gradientu prostego) upatrywaliśmy przyczyn jego złego zachowania – zygzakowania – w braku pamięci. Wzór (4.7) określający nowy kierunek poprawy jest realizacją pierwszego z zaproponowanych podejść mających temu zaradzić – dodaniu poprawki zależnej od historii, ponieważ wiąże nowy kierunek poprawy z poprzednim kierunkiem poprawy, a także poprzez współczynnik (k) wyliczany wg wzoru (4.9) z gradientem obliczonym w kroku poprzednim. Ponieważ w kroku 4 nie możemy zapewnić dokładnej minimalizacji w kierunku, to okazało się, że kierunki wyznaczone w ten sposób mogą „prowadzić na manowce” – w tę stronę gdzie funkcja celu maleje powoli. Wobec tego aby zabezpieczyć się przed taką sytuacją, lub ją przerwać („oczyścić” pamięć) gdy już wystąpiła, przyjęto że odnowa następuje gdy od poprzedniej „upłynęło” n kroków. Wybór długości okresu, po którym następuje odnowa jako równego ilości zmiennych jest w zasadzie wyborem heurystycznym i odnosi się do zadań o dużej wymiarowości (kilkanaście zmiennych). Dla zadań o kilku zmiennych zręczniej jest dokonywać odnowy co 3n lub co 2n kroków, ponieważ z odnową co n kroków działanie algorytmu dla takich zadań może różnić się niewiele od działania algorytmu największego spadku.

• Zauważmy, że przy dokładnej minimalizacji w kierunku wzory Fletchera – Reevesa (4.8) i Poljaka – Polaka – Ribière’a (4.9) dają tą samą wartość współczynnika $\beta ^{(k)}$, ponieważ wtedy

$∇f(x^ {(k)})∇^T f(x^ {(k-1)})=0,  k=1,2,...$(patrz wzór (4.2)),

a więc odjemnik w liczniku wzoru (4.9) jest równy zeru:

$∇f(x^ {(k)})(∇^T f(x^ {(k)})-∇^T f(x^ {(k-1)}))=∇f(x^ {(k)})∇^T f(x^ {(k)})-∇f(x^ {(k)})∇^T f(x^ {(k-1)}))=∇f(x^ {(k)})∇^T f(x^ {(k)})$.

Dlaczego wybraliśmy wersję Poljaka – Polaka – Ribière’a (Rosjanina B.T. Poljaka, Amerykanina E. Polaka i Francuza G. Ribière) (4.9) a nie Fletchera – Reevesa (4.8)?

Ponieważ testy różnych wersji wzoru określającego wpływ poprzedniego kierunku poprawy na kierunek bieżący (zaproponowano ich więcej niż tylko przedstawione dwa wyrażenia) pokazały, że algorytm posługujący się wzorem Poljaka – Polaka – Ribière’a częściej znajduje rozwiązanie w mniejszej liczbie iteracji aniżeli algorytm ze wzorem Fletchera – Reevesa. Ponadto częściej potrafi znaleźć rozwiązanie w sensownej liczbie iteracji przy obniżonej dokładności minimalizacji w kierunku – jest więc bardziej odporny błędy wyznaczania kolejnych punktów. Formalnego wyjaśnienia tego faktu nie ma. 

M.J.D. Powell przedstawił następującą hipotezę. Ponieważ minimalizowana funkcja nie jest kwadratowa i minimalizacja w kierunku nie jest dokładna, to przy minimalizacji wielu funkcji celu mamy do czynienia z sytuacją, w której kolejne kroki są coraz krótsze – $x^{(k)}$ leży coraz bliżej $x^{(k–1)}$, algorytm rusza się coraz wolniej, jak się często mówi – grzęźnie. Bliskość kolejnych punktów oznacza, że gradienty w nich wyliczane są prawie takie same: $∇f(x^ {(k)})≈∇f(x^ {(k-1)})$.Dla formuły Fletchera – Reevesa (4.8) mamy więc $β^ {(k)}≈1.$ Natomiast dla formuły Poljaka – Polaka – Ribière’a (4.9) dostajemy  $β^ {(k)}≈0$, co daje $d^ {(k)}≈-∇^T f(x^ {(k)})$ Algorytm ma zdolność do samo-odnowy w sytuacji ugrzęźnięcia. Takiej własności dla implementacji algorytmu ze wzorem Fletchera – Reevesa nie zaobserwowano.

Ponieważ odnowa – ruch w kierunku antygradientu – następuje wtedy gdy wyznaczony według wzoru (4.7) kierunek przestaje być kierunkiem poprawy, a także gdy od ostatniej odnowy „upłynęło” n kroków, to w nieskończonym ciągu $\left\{x^ {(k)}\right\}$ generowanym przez algorytm zawiera się nieskończony podciąg $\left\{ x^{(j)}\right \}_{j \in J}$ punktów wyznaczonych na kierunkach określonych przez stosowne antygradienty $–∇f (x^{(j–1)})$. Zatem twierdzenie określające warunki dające zbieżność algorytmu gradientu sprzężonego jest podobne do twierdzenia dla algorytmu gradientu prostego. 

Przy odpowiednio mocniejszych założeniach o funkcji wyboru oraz wymaganiu dokładnej minimalizacji w kierunku, można pokazać, że algorytm ten zbiega superliniowo do punktu minimalizującego. 

Powiedzieliśmy, że algorytm gradientu sprzężonego jest lepszy od algorytmu największego spadku. Aby nie być gołosłownym musimy teraz to pokazać.

PRZYKŁAD 4.2 
Wyniki testów muszą być porównywalne, rozważmy więc tą samą funkcję dwu zmiennych co w Przykładzie 8.2:

$(x_1,x_2)↦f(x_1,x_2)=(x_1-2)^4+(x_1-2x_2 )^2$

 

Rys. 4.14  8.7: Trajektoria algorytmu gradientu sprzężonego

Na rysunku zaznaczono kolorem zielonym „drogę” algorytmu gradientu sprzężonego z metodą interpolacji kwadratowej użytą do minimalizacji w kierunku, który wystartował z tego samego co poprzednio punktu początkowego $x^ {(0)}=(0,3)$ i miał znaleźć rozwiązanie z dokładnością $\varepsilon = 0.05$ (przypominamy, że dla algorytmu gradientu prostego wybrana dokładność była 2 razy mniejsza i wynosiła 0.1). Dla porównania kroki algorytmu największego spadku zaznaczono na czerwono.
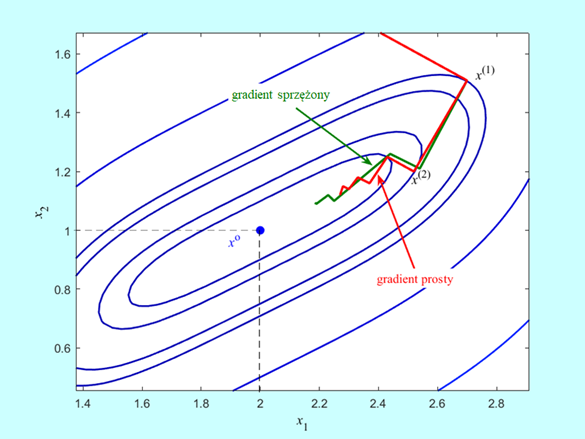
Algorytm wykonał siedem kroków i zatrzymał się w punkcie $x^{(7)} = (2.185,1.094)$ w którym $‖∇f(2.185,1.094)‖=0.02$, wartość funkcji celu $f (2.185,1.094) = 0.0012$, a odległość proponowanego rozwiązania od punktu optymalnego jest równa  $‖x^{(7)}-x^o ‖=0.208$ (w Przykładzie 4.1 była równa 0.3).
Krok pierwszy z $x^ {(0)}=(0,3)$ do $x^ {(1)}=(2.70,1.51)$ był oczywiście taki sam jak dla metody gradientu prostego. Przejście z kroku szóstego do siódmego jest na rysunku niezauważalne, ponieważ $x^{(6)} = = (2.190,1.090)$ a $x^{(7)} = (2.185,1.094)$. Zadanie jest dwuwymiarowe, zatem odnowa (ruch w kierunku antygradientu) nastąpiła w kroku trzecim, piątym i ostatnim – siódmym. Ponieważ punkty $x^{(2)}$ wyznaczone w drugim kroku przez oba algorytmy leżą jeszcze blisko siebie to i antygradienty są prawie równe, więc ruch obu algorytmów w trzecim kroku musi dać punkty $x^{(3)}$, które też będą leżały blisko siebie. Lecz antygradient policzony w punkcie $x^{(3)}$ wyliczonym przez algorytm najszybszego spadku jest równy $[-0.18⋮-0.28]$, a kierunek poprawy wyznaczony w swoim punkcie $x^({3)}$ przez algorytm gradientu sprzężonego jest równy $[-0.30⋮-0.25]$. Ta różnica spowodowała, że algorytm gradientu sprężonego wyznaczył jako punkt $x^{(4)}$ punkt o współrzędnych $(2.25,1.10)$, co dało wartość funkcji celu $f (2.25,1.10) = 0.0064$, a algorytm gradientu prostego – punkt o współrzędnych $(2.37,1.16)$ z wartością funkcji celu $f (2.37,1.16) = 0.02$. W piątym kroku algorytm gradientu sprzężonego wyznaczył punkt $x^{(5)} = (2.23,1.12)$ dający wartość funkcji celu $f (2.23,1.12) = 0.003$ i wartość normy gradientu $‖∇f(2.23,1.12)‖=0.05$, a więc punkt lepszy niż ostatni (ósmy) punkt uzyskany przez algorytm najszybszego spadku (przypominamy był to punkt $(2.27,1.12)$ w którym $f (2.27,1.12) = 0.0062$, oraz $‖∇f(2.27,1.12)‖=0.09)$. 
Algorytm gradientu sprzężonego (z za częstą odnową) zatrzymał się w punkcie oddalonym od rozwiązania o nieco ponad 0.02 z wartością funkcji celu większą od optymalnej o 0.0012 (algorytm prostego gradientu osiągnął, odległość – 0.09 i wartość większa od minimalnej o 0.0062). Okazał się wiec lepszy od współzawodnika, ale też nie bardzo poradził sobie z praktyczną utratą ścisłej wypukłości przez funkcję celu.

A jak algorytm gradientu sprzężonego poradził sobie ze znalezieniem minimum funkcji Rosenbrocka ?

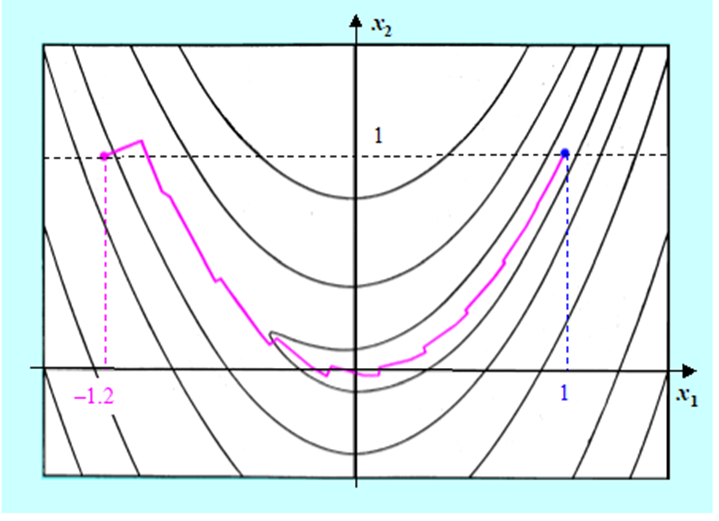
Rysunek pokazuje kolejne kroki algorytmu gradientu sprzężonego bez odnowy (bo funkcja Rosenbrocka jest dwuwymiarowa) i z minimalizacją w kierunku wykorzystującą wielomian interpolacyjny. Widać, że Algorytm wykonał 24 iteracje poruszając się po dnie doliny bez zygzakowania (8 iteracji), dobrze przebył zakręt (8 iteracji) a następnie dość szybko „pomaszerował” w kierunku punktu minimalizującego (8 iteracji). Zastosowana modyfikacja gradientu w tym teście się sprawdziła. Widać jednak, że dla twórców algorytmów trudniej jest nauczyć Algorytm jak ma sobie poradzić z „rozpłaszczeniem się rzeźby terenu” niż z zaproponowaniem efektywnej metody poruszania się „w krętych wąskich dolinach”.

Jak już powiedzieliśmy algorytm gradientu sprzężonego jest realizacją pierwszego z zaproponowanych podejść wzbogacenia algorytmu gradientu prostego w pamięć – dodaniu poprawki zależnej od historii. Zastanówmy się teraz nieco głębiej nad tym jak ta zależność od historii wygląda.

Przepiszmy wzór z piątego kroku określający kolejne punkty generowane przez algorytm gradientu sprzężonego (zapominając o potencjalnej odnowie wynikającej z nie wygenerowania kierunku poprawy rozpoczynanej w trzecim kroku algorytmu), a także wyrażenia określające jego poszczególne składniki (przyjmujemy, że $n \geq 3)$

$x^{(k+1)}=x^ {(k)}+α^ {(k)} (-∇^T f(x^ {(k)})+β^ {(k)} d^ {(k-1)}), \,k=1,...,n-1,      (\star)$

$β^ {(k)} =\dfrac{∇f(x^ {(k)})(∇^T f(x^ {(k)})-∇^T f(x^ {(k-1)}))}{∇f(x^ {(k-1)})∇^T f(x^ {(k-1)})}.  \qquad (4.9)$

$d^ {(0)}=-∇^T f(x^ {(0)})$

$d^ {(k-1)}=-∇^T f(x^{(k-1) })+β^{(k-1) }d^{(k-2)},\, k=2,...,n-1$

Widać, że algorytm ma dwa rodzaje pamięci zawarte w składniku $β^ {(k)} d^ {(k-1)}$ wzoru $\star).$

• Pierwszą, potrzebną do obliczenia bieżącej wartości współczynnika skalującego

$β^ {(k)}=\mathfrak{B} (∇f(x^ {(k)}),∇f(x^ {(k-1)})).$

Jej stan $β$ nie zależy od wartości tego współczynnika w kroku poprzednim, a z wielkości wyznaczonych uprzednio wykorzystuje tylko gradient. Taką pamięć można nazwać krótkookresową, bo nie ma w niej efektu kumulacji informacji zawartej w stanach poprzednich współczynnika skalującego.

• Drugą – określoną przez sposób obliczania kierunków poprawy

$d^ {(k-1)}=\mathfrak{C} (∇f(x^ {(k-1)}),β^ {(k-1)}),d^{(k-2)}).$

Po pierwsze, jej stan d jest w naturalny sposób opóźniony o takt (kierunek poprawy w takcie k możemy obliczyć tylko na podstawie kierunku wyznaczonego w takcie poprzednim). Bieżący stan tej pamięci zależy od jej stanu poprzedniego, co wobec tego że wzór $(\star)$ jest sumą oznacza, że w kolejnym wektorze kierunku poprawy jest w swoisty sposób „podsumowywana” cała dotychczasowa historia działania algorytmu. Jest to więc pamięć długookresowa. Kumulacja niedokładności obliczeniowych w tej pamięci może powodować, wspomniane wyżej „prowadzenie na manowce”. Odnowa, to oczyszczenie pamięci długookresowej ze złej informacji i wprowadzenie do niej kierunku, o którym wiemy, że na pewno jest kierunkiem poprawy.