Podręcznik: Model neuronów samoorganizujących się poprzez współzawodnictwo

1. Modele neuronów

1.5. Model neuronów samoorganizujących się poprzez współzawodnictwo

Specjalny typ stanowią neurony samoorganizujące się poprzez konkurencję. W klasycznym ujęciu mają one stopień wejściowy w postaci standardowego sumatora wagowego o wagach

$w_{ij}$ (rys. 1.6), dla którego sygnał wyjściowy

$i$ -tego sumatora opisany jest relacją

$u_i = \sum_{j=1}^N w_{ij} x_j = \mathbf{w}_i^T \mathbf{x} = \mathbf{x}^T \mathbf{w}_i$

(1.15)

w której x jest znormalizowanym $N$ -wymiarowym wektorem wejściowym a $\mathbf{w}_i$ wektorem wagowym $i$ -tego neuronu.

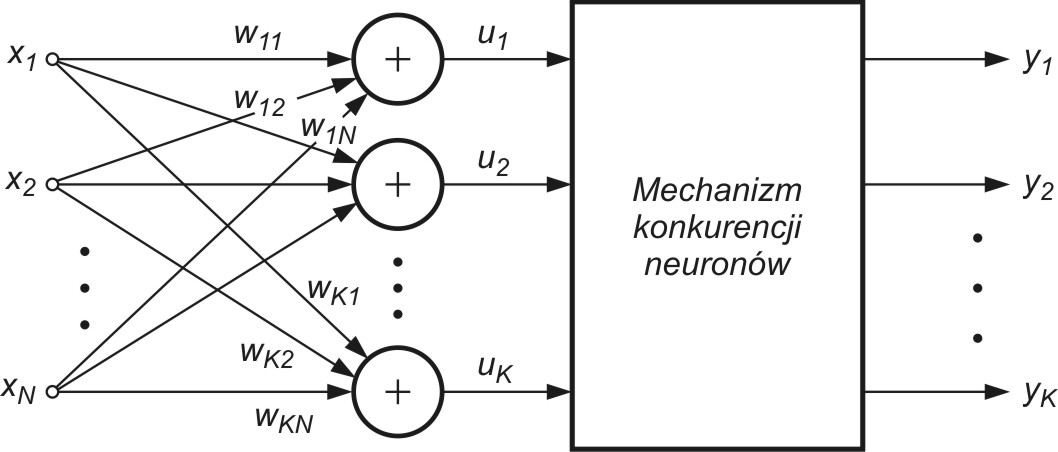
Rys. 1.6 Model neuronów współzawodniczących ze sobą

Grupa neuronów współzawodniczących ze sobą pobudzana jest tymi samymi sygnałami wejściowymi $\mathbf{x}_j$ . W zależności od aktualnych wartości sygnałów sumacyjnych $\mathbf{u}_i$ poszczególnych neuronów za zwycięzcę uważa się neuron, którego wartość $\mathbf{u}_i$ jest największa. Neuron zwycięzca przyjmuje na swoim wyjściu stan $1$ , a pozostałe (przegrywające) stan zero. Ze względu na normalizację sygnałów wejściowych neuronem zwycięskim jest zawsze ten, który znajduje się najbliżej aktualnego wektora wejściowego $\mathbf{x}$ , a więc o najmniejszej wartości normy $d(\mathbf{x},\mathbf{w_i}) = \Vert \mathbf{x} - \mathbf{w}_i \Vert$ . W praktyce zamiast obliczać sumy wagowe poszczególnych neuronów w procesie wyłaniania zwycięzcy oblicza się miary odległościowe i na tej podstawie wyłania zwycięzcę [46]. Najprostsza adaptacja wag neuronów jest typu WTA (ang. Winner Takes All) i nie wymaga nauczyciela. Na wstępie przyjmuje się losowe, znormalizowane wartości wag poszczególnych neuronów. Po podaniu wektora wejściowego $\mathbf{x}$ wyłaniany jest zwycięzca. Neuron zwyciężający w konkurencji przyjmuje stan 1, a pozostałe 0. Aktualizacja wag odbywa się według wzoru Grosberga zapisanego w formie skalarnej dla $j$ -tej wagi wektora $i$ -tego

$w_{ij} (k+1) = w_{ij} (k) + \eta [ x_j - w_{ij}(k) ]$

(1.16)

lub wektorowej

$\mathbf{w}_{i} (k+1) = \mathbf{w}_{i} (k) + \eta [ \mathbf{x} - \mathbf{w}_{i}(k) ]$

(1.17)

Zauważmy, że w formule WTA jedynie neurony zwycięskie o sygnale wyjściowym $y_i = 1$ uaktualniają swoje wagi. Neurony przegrywające konkurencję nie zmieniają swoich wag. W efekcie takiej organizacji algorytmu uczącego wektory wagowe neuronów podążają za wektorami uczącymi $\mathbf{x}$ , przyjmując w efekcie uśrednione wartości wektorów wejściowych, dla których dany neuron był zwycięzcą. W praktyce stosuje się również strategię WTM (Winner Takes Most), w której neurony przegrywające konkurencję uczestniczą również w adaptacji swoich wag, ale przy współczynniku adaptacji $\eta$ uzależnionym od odległości tych neuronów od wektora wejściowego $\mathbf{x}$ .

W wyniku zwycięstwa neuronu następuje douczenie jego wag, przybliżające je do odpowiednich składowych danego wektora $\mathbf{x}$ . Przy podaniu na wejście sieci wielu wektorów zbliżonych do siebie, zwyciężać będzie ciągle ten sam neuron, w wyniku czego jego wagi odpowiadać będą uśrednionym wartościom wektorów wejściowych, dla których dany neuron był zwycięzcą. Neurony przegrywające nie zmieniają swoich wag. Dopiero zwycięstwo przy następnej prezentacji wektora wejściowego umożliwi im dokonanie aktualizacji wag i rozpoczęcie procesu douczania przy kolejnych zwycięstwach. W efekcie takiego współzawodnictwa następuje automatyczne grupowanie danych. Neurony dopasowują swoje wagi w ten sposób, że przy prezentacji grup wektorów wejściowych zbliżonych do siebie zwycięża zawsze ten sam neuron. Neuron ten reprezentować będzie swoimi wagami wszystkie wektory $\mathbf{x}$ znajdujące się w jego strefie dominacji. W efekcie powstaje samoczynny podział danych na klastry reprezentowane przez neuron zwycięzcę. Układy tego typu są stosowane najczęściej do grupowania danych jak również do klasyfikacji wektorów.