Podręcznik
1. Modele neuronów
1.6. Model neuronu Hebba
Donald O. Hebb, badając działanie komórek nerwowych [24] zauważył, że powiązanie wagowe dwóch komórek jest wzmacniane, jeśli obie komórki są jednocześnie pobudzone (stają się aktywne). Jeśli \( j \)-ta komórka o sygnale wyjściowym \( y_j \) powiązana jest z \( i \)-tą o sygnale wyjściowym \( y_i\) przez wagę \( w_{ij} \), wówczas na stan powiązań tych komórek wpływają wartości ich sygnałów \( y_j \) oraz \( y_i \).
D. Hebb zaproponował regułę matematyczną, w której uwzględniony został wynik tej obserwacji. Zgodnie z regułą Hebba, zmiana wagi \( w_{ij}\) neuronu odbywa się proporcjonalnie do iloczynu jego sygnału wejściowego oraz wyjściowego [46]
| \( w_{ij} (k+1) = w_{ij} (k) + \eta y_i y_j \) |
(1.18) |
przy współczynniku \(\eta\) reprezentującym wartość stałej uczenia. Reguła Hebba może być stosowana do różnego typu struktur sieci neuronowych i różnych funkcji aktywacji zastosowanych w modelu neuronu.
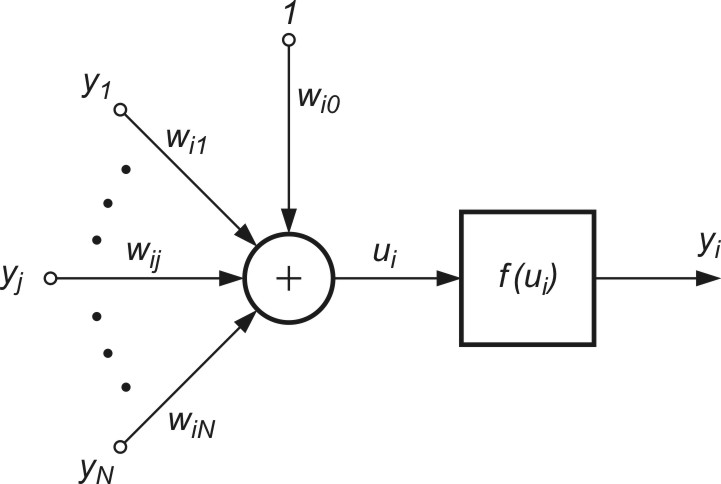
Ogólny model neuronu Hebba, przedstawiony na rys. 1.7, odpowiada standardowej postaci modelu. Waga \( w_{ij} \) włączona jest między sygnałem wejściowym \( y_j \) a węzłem sumacyjnym \( i \)-tego neuronu o sygnale wyjściowym \( y_i \).
Uczenie neuronu z zastosowaniem reguły Hebba może się odbywać w trybie bez nauczyciela lub z nauczycielem. W pierwszym przypadku w regule Hebba używa się aktualnej wartości \( y_i \) sygnału wyjściowego neuronu (wzór (1.18)). W uczeniu z nauczycielem wartość sygnału wyjściowego \( y_i \) zastępuje się wartością zadaną \( d_i \) dla tego neuronu. Regułę Hebba można wówczas zapisać w postaci
| \( w_{ij} (k+1) = w_{ij} (k) + \eta d_i y_j \) |
(1.19) |
Reguła Hebba charakteryzuje się tym, że w jej wyniku wagi mogą przybierać wartości dowolnie duże i nie podlegają stabilizacji, gdyż w każdym cyklu uczącym następuje proces sumowania aktualnych przyrostów wartości wag.
Jedną z metod poprawy stabilności procesu uczenia według reguły Hebba jest przyjęcie przy aktualizacji wag nie ostatniej wartości \( w_{ij} \) ale wartości zmniejszonej o tak zwany współczynnik zapominania \( \gamma \) Wówczas regułę Hebba można zapisać w postaci
| \( w_{ij} (k+1) = (1-\gamma) w_{ij} (k) + \eta y_i y_j \) |
(1.20) |
Współczynnik zapominania \(\gamma\) zawiera się zwykle w przedziale (0, 1) i stanowi najczęściej niewielki procent stałej uczenia \(\eta\). Przyjęcie dużej wartości \(\gamma\) powoduje, że neuron zapomina większość tego, co zdołał nauczyć się w przeszłości. Uczenie Hebba zaliczane jest do uczenia typu korelacyjnego, gdyż w swojej istocie uwzględnia korelacje zachodzące między sygnałami neuronów sieci.
Stabilizacja reguły Hebba przez wprowadzenie współczynnika zapominania zawodzi w przypadku neuronu liniowego. Dla neuronu liniowego Hebba jego sygnał wyjściowy opisany jest zależnością linową \(y_i=\mathbf{w}_i^T \mathbf{x}=\mathbf{x}^T \mathbf{w}_i\), w której \( \mathbf{w}_i\) jest wektorem wagowym neuronu \(i\)-tego a \( \mathbf{x}\) wektorem sygnałów wejściowych tego neuronu. Zostało udowodnione, że w takim przypadku wartości wag \( \mathbf{x}\) procesie uczenia nigdy nie stabilizują się, a proces uczenia się nie kończy. Stabilizacja wag (połączona z jednoczesną normalizacją) jest możliwa przez wprowadzenie modyfikacji reguły Hebba. Zgodnie z modyfikacją zaproponowana przez E. Oję [46] aktualizacja wag \( w_{ij} \) wektora \( \mathbf{w}_i\) przebiega według wzoru
| \( w_{ij} (k+1) = w_{ij} (k) + \eta ( x_j - w_{ij} y_i ) \) |
(1.21) |
Reguła ta przypomina propagację wsteczną, gdyż sygnał \(x_j\) jest modyfikowany przez sygnał wsteczny, pochodzący od sygnału wyjściowego \(y_i\) neuronu. Przy jednym neuronie reguła Oji jest regułą lokalną, gdyż w procesie modyfikacji sygnału \(x_j\) bierze udział tylko waga, którą aktualnie adaptujemy.
