Podręcznik: Struktura sieci wielowarstwowej MLP

2. Sieć perceptronu wielowarstwowego MLP

2.2. Struktura sieci wielowarstwowej MLP

Sieć wielowarstwową MLP tworzą neurony ułożone w warstwach połączonych kolejno między sobą, przy czym oprócz warstwy wejściowej i wyjściowej istnieje co najmniej jedna warstwa ukryta.

a)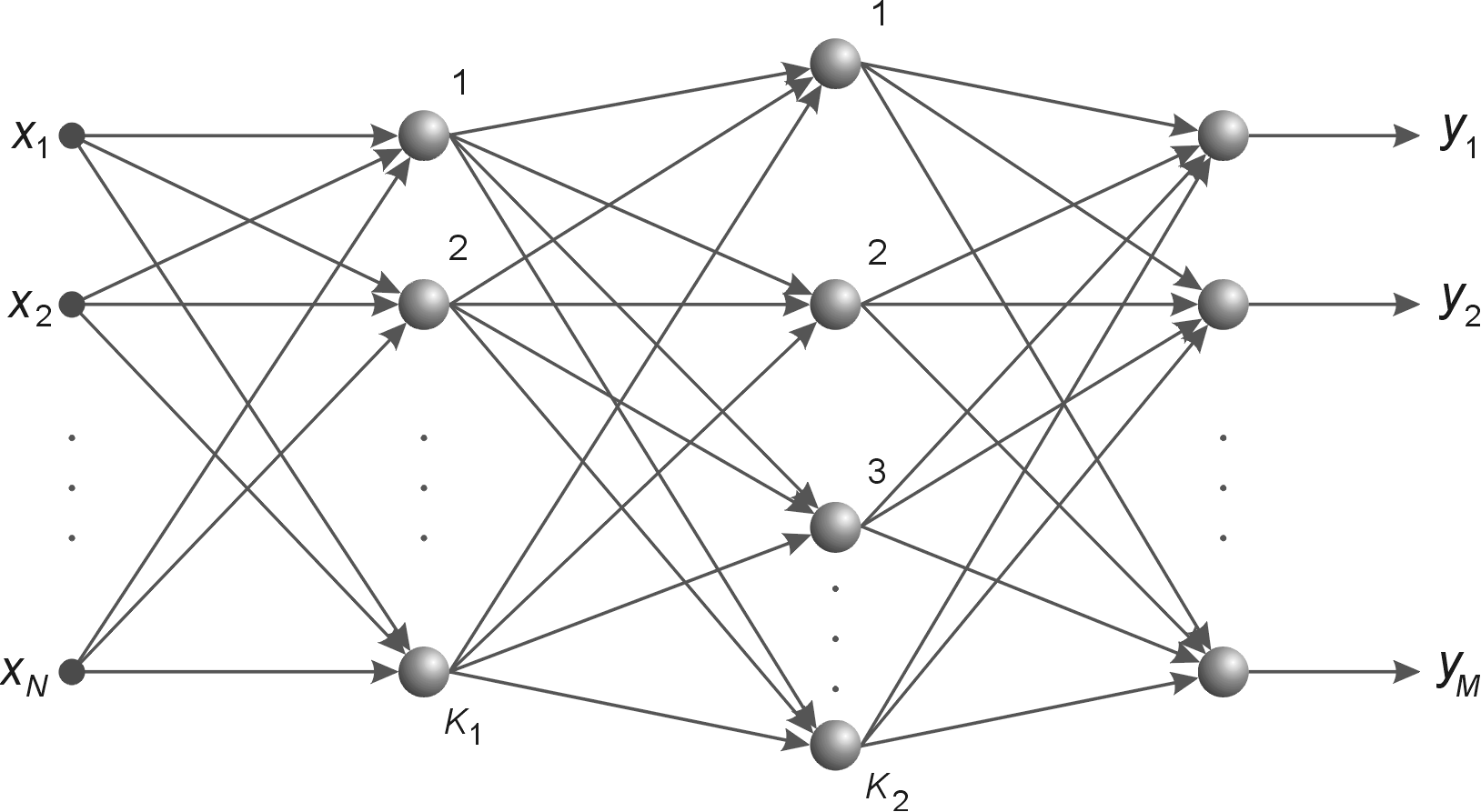
b)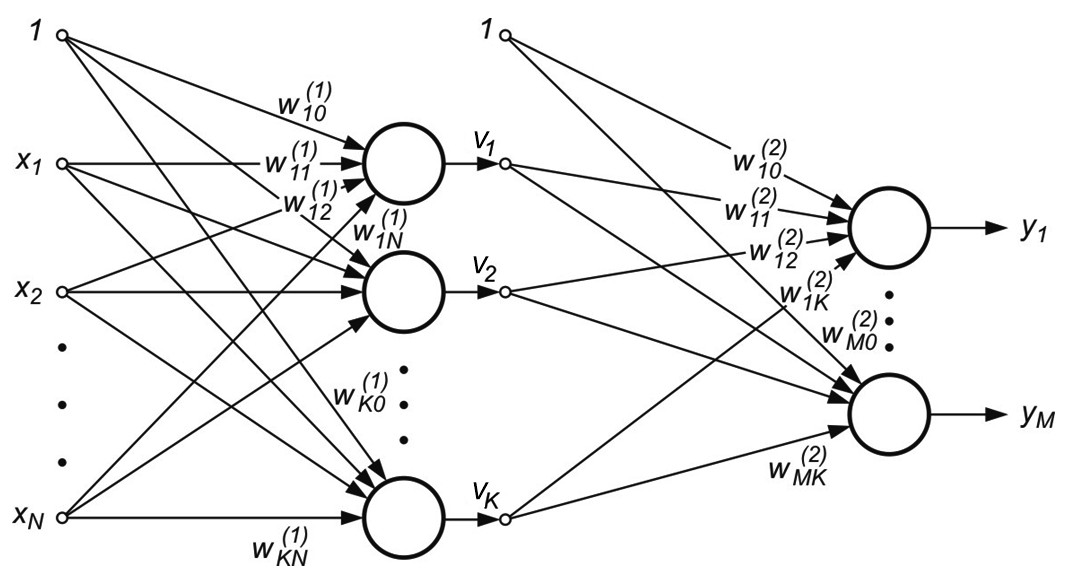

Rys. 2.1 a) Ogólny schemat sieci neuronowej sigmoidalnej o dwu warstwach ukrytych, b) sieć o jednej warstwie ukrytej z oznaczeniem połączeń wagowych i polaryzacją

Na rys. 2.1b przedstawiono sieć o jednej warstwie ukrytej [46]. Połączenia międzyneuronowe występują jedynie między sąsiednimi warstwami (w kierunku od wejścia do wyjścia). Stosowane będą oznaczenia sygnałów i wag zgodnie z rysunkiem. Wagi neuronów warstwy ukrytej otrzymają wskaźnik górny (1), natomiast warstwy wyjściowej wskaźnik (2). Sygnały wyjściowe neuronów warstwy ukrytej oznaczone są symbolem $v_j (j=1, 2, \ldots, K)$ , a warstwy wyjściowej symbol $y_j (j=1, 2, \ldots, M)$ . Zakłada się, że funkcja aktywacji neuronów jest dana w postaci sigmoidalnej unipolarnej bądź bipolarnej. Dla uproszczenia oznaczeń przyjęte będzie rozszerzone oznaczenie wektora wejściowego $\textbf{x}$ sieci w postaci $\textbf{x}=[x_0, x_1, x_2, \ldots, x_N]^T$ , w którym $x_0=1$ oznacza sygnał jednostkowy polaryzacji. Z wektorem $\textbf{x}$ są związane dwa wektory wyjściowe sieci: wektor aktualny $\textbf{y}=[y_1, y_2, \ldots, y_M]^T$ oraz wektor zadany $\textbf{d}=[d_1, d_2, \ldots, d_M]^T$ .

Celem uczenia jest określenie wartości wag $w_{ij}^{(1)}$ oraz $w_{ij}^{(2)}$ wszystkich warstw sieci w taki sposób, aby przy zadanym wektorze wejściowym $\textbf{x}$ uzyskać na wyjściu wartości sygnałów wektora $\textbf{y}$ odpowiadające z dostateczną dokładnością wartościom zadanym reprezentowanym przez wektor $\textbf{d}$ . Traktując jednostkowy sygnał polaryzujący jako jedną ze składowych wektora wejściowego $\textbf{x}$ , wagi polaryzacji można włączyć do wektora wag poszczególnych neuronów obu warstw. Przy takim oznaczeniu sygnał wyjściowy $i$ -tego neuronu warstwy ukrytej daje się opisać wzorem

$v_i=f\left(\sum_{j=0}^N w_{i j}^{(1)} x_j\right)$

(2.1)

w której wskaźnik $j=0$ odpowiada sygnałowi oraz wagom polaryzacji. W przypadku warstwy wyjściowej $k$ -ty neuron wytwarza sygnał wyjściowy opisany następująco

$y_k=f\left(\sum_{i=0}^K w_{k i}^{(2)} v_i\right)=f\left(\sum_{i=0}^K w_{k i}^{(2)} f\left(\sum_{j=0}^N w_{i j}^{(1)} x_j\right)\right)$

(2.2)

Powyższy wzór reprezentuje formułę tak zwanego uniwersalnego aproksymatora, gdyż definiuje jawną postać funkcji aproksymującej, realizowanej przez sieć. Jak wynika z zależności (2.2), na wartość sygnału wyjściowego mają wpływ wagi obu warstw, których właściwy dobór pozwala dopasować wartości funkcji aproksymującej do wielkości zadanych ( $\textbf{x}$ , $\textbf{d} )$ .