Podręcznik
2. Sieć perceptronu wielowarstwowego MLP
2.9. Program MLP do uczenia sieci wielowarstwowej
W wykładzie tym przedstawimy program MLP uczenia i użytkowania w trybie testującym sieci MLP. Program ten w postaci interfejsu graficznego został stworzony na bazie oprogramowania neuronowego toolboxu „Neural Network” Matlaba. Przedstawimy szczegóły dotyczące tego interfejsu, podstawowe opcje wykorzystania programu oraz wyniki testu na aproksymacji danych wielowymiarowych.
2.9.1 Opis programu
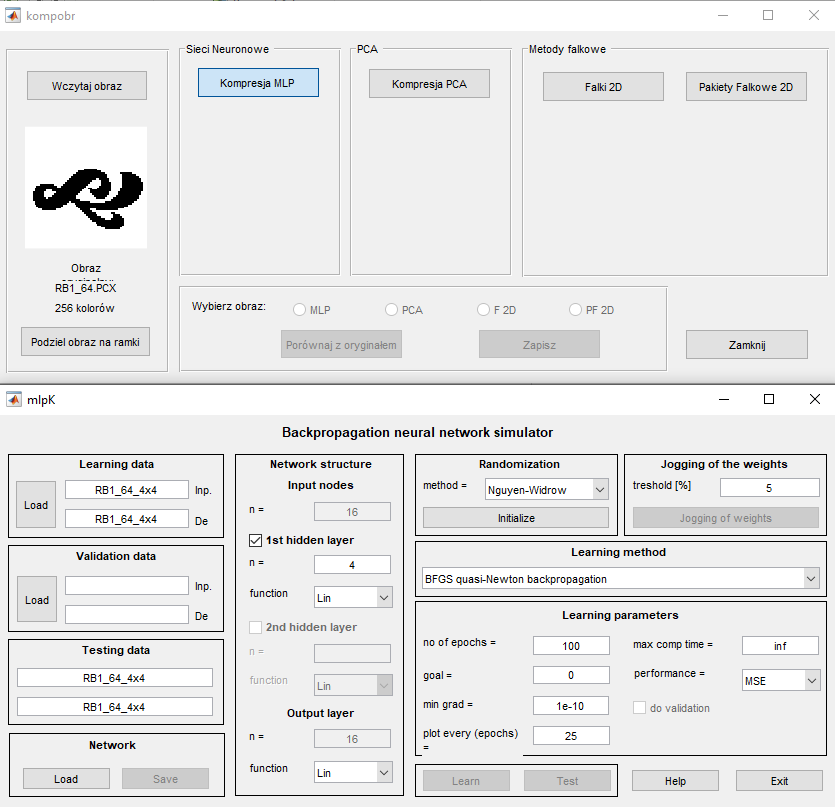
Wykorzystując toolbox "Neural Network" i inne funkcje wbudowane w programie Matlab zaimplementowano wszystkie wymienione w wykładzie trzecim algorytmy uczące w postaci pakietu programów pod nazwą MLP (plik uruchomieniowy mlp.m). Uruchomienie programu następuje w oknie komend Matlaba po napisaniu nazwy mlp programu. Pojawi się wówczas menu główne przedstawione na rys. 5.1 [46].
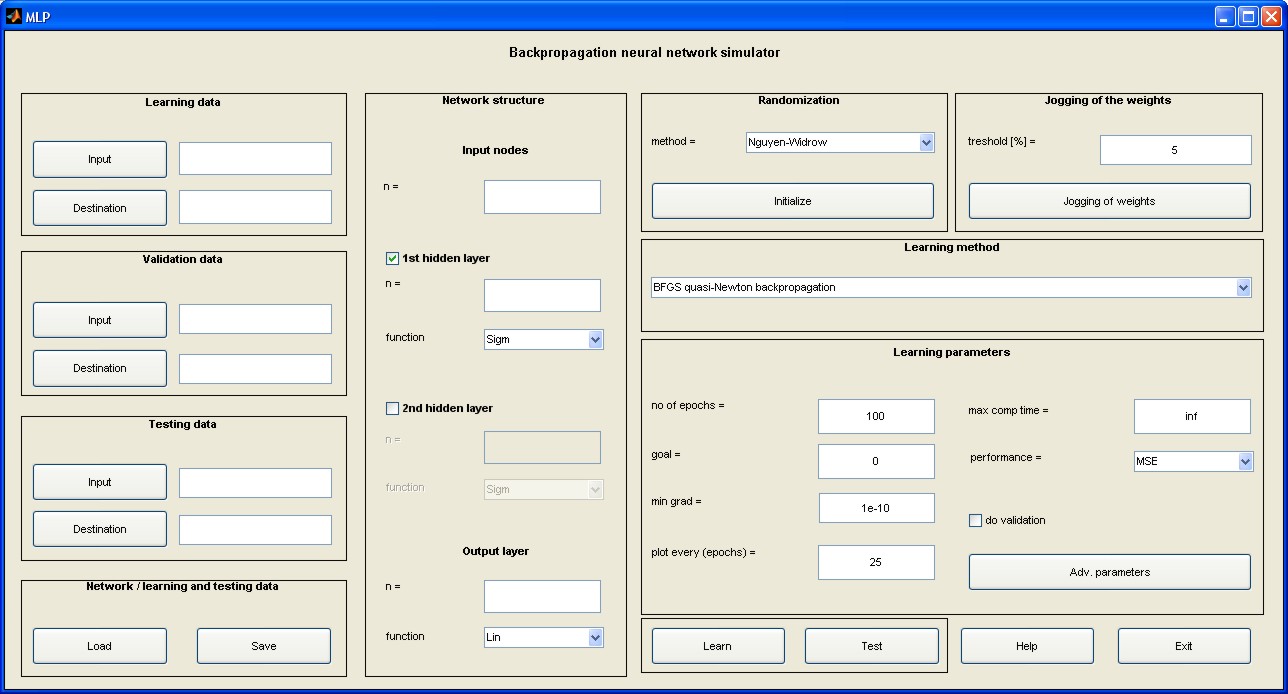
W lewej części menu znajdują się: pole do zadawania danych uczących (pole Learning data), weryfikujących (pole Validation data) oraz testujących, nie uczestniczących w uczeniu (pole Testing data). Przycisk Input służy do wczytania nazwy pliku z rozszerzeniem .mat zawierającego zbiór wektorów \( \textbf{x} \) zorganizowany w formie macierzy (liczba wierszy odpowiada liczbie tych wektorów, a liczba kolumn jest równa wymiarowi wektora \( \textbf{x} \)). Przycisk Destination pozwala na podanie nazwy pliku, również z rozszerzeniem .mat, zawierającego zbiór wektorów zadanych \( \textbf{d} \) stowarzyszonych z wektorami wejściowymi \( \textbf{x} \). Można również zapamiętać całą sesję uczącą (przycisk Save) lub załadować jej zawartość wcześniej zapamiętaną (przycisk Load). Po naciśnięciu przycisku Load pojawia się okno dialogowe menu wyboru struktury sieci i danych przedstawione na rys. 2.5 (xu – macierz zawierająca zbiór wektorów uczących \( \textbf{x}_u \), xt – macierz zawierająca zbiór wektorów testujących \( \textbf{x}_t \), du - macierz zawierająca zbiór zadanych (znanych) wektorów uczących \( \textbf{d}_u \) na wyjściu sieci stowarzyszonych z wektorami \( \textbf{x}_u \), dt - macierz zawierająca zbiór zadanych wektorów testujących \( \textbf{d}_t \) na wyjściu sieci stowarzyszonych z wektorami \( \textbf{x}_t \).
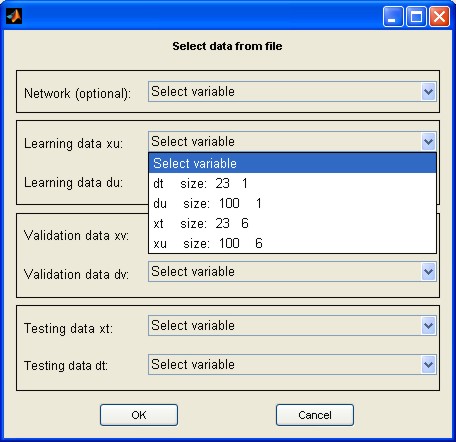
Wybierając nazwę wcześniej zapisanej struktury sieci można podać plik zawierający kompletne dane sieci MLP zapisane w poprzedniej sesji uczącej. Można również wybrać opcję wczytywania danych uczących, weryfikujących i testujących zapisanych w jednym wspólnym pliku, z wyróżnionymi nazwami odpowiednich zmiennych.
Definiowanie struktury sieciowej odbywa się w polu środkowym menu (pole Network structure). Należy wybrać liczbę warstw ukrytych (dostępne są dwie) oraz liczbę neuronów w każdej warstwie, jak również rodzaj funkcji aktywacji neuronów. Dostępne są następujące funkcje: liniowa (Lin), sigmoidalna jednopolarna (Sigm) oraz sigmoidalna bipolarna (Bip). Liczba węzłów wejściowych oraz neuronów wyjściowych są automatycznie wyznaczane na podstawie wymiaru wektorów \( \textbf{x} \) oraz \( \textbf{d} \) i użytkownik nie może ich zmienić.
Przed rozpoczęciem uczenia należy dokonać inicjalizacji wag sieci (pole Randomization) naciskając przycisk Initialize. W programie zaimplementowano specjalną metodę randomizacji Ngyen-Widrowa [43]. Przy utknięciu procesu uczenia w minimum lokalnym można dokonać losowej zmiany wag przez naciśnięcie przycisku Jogging of weights w polu Jogging of weights i kontynuacji uczenia z nowego punktu startowego wag. Przedtem należy ustawić zakres randomizacji (threshold).
Przed uruchomieniem procesu uczenia należy jeszcze ustawić wartości parametrów procesu w polu Learning parameters, w tym liczby cykli uczących (no of epochs), wartości oczekiwanej optymalnej wartości funkcji celu (goal), minimalnej wartości gradientu (min grad) kończącej proces uczenia, maksymalnego czasu uczenia (max comp time), a także sposobu definiowania funkcji celu (performance). Dostępne są następujące miary funkcji celu: MSE - wartość średnia sumy kwadratów błędów (Mean Squared Error) - zalecana, SSE - suma kwadratów błędów (Sum Squared Error), MAE - wartość średnia błędów absolutnych (Mean Absolute Error).
W trakcie uczenia program automatycznie wykreśla wartości aktualne funkcji celu z krokiem wybranym w polu plot every (epochs). Przy wielokrotnej kontynuacji procesu uczenia tworzony jest dodatkowy zbiorczy wykres postępów minimalizacji funkcji celu. Jeżeli w procesie uczenia przewiduje się weryfikację działania sieci na danych weryfikujących, należy uaktywnić przycisk do validation. Przy takim wyborze jednocześnie z krzywą uczenia wykreślany jest aktualny błąd dla danych weryfikujących.
Uruchomienie procesu uczenia sieci odbywa się przez naciśnięcie przycisku Learn, a sprawdzenie działania sieci na danych testujących poprzez naciśnięcie przycisku Test. Po zakończeniu procesu uczenia program automatycznie przeprowadza symulację działania na danych uczących odtwarzając sygnały wyjściowe w postaci zbioru wektorów \( \textbf{y} \) odpowiadających wymuszeniom zawartym w zbiorze wektorów \( \textbf{x} \) użytych w uczeniu. Aktualne odpowiedzi sieci zarówno na danych uczących jak i testujących przypisane są zmiennej \( y \) i są dostępne na bieżąco w polu roboczym Matlaba.
2.9.2 Przykład aproksymacji funkcji za pomocą sieci MLP
Problemem testowym jest jednoczesna aproksymacja czterech funkcji przedstawionych na rys. 2.6. Są to funkcje: prostokątna, trójkątna, sinusoidalna oraz wartość absolutna funkcji sinc.
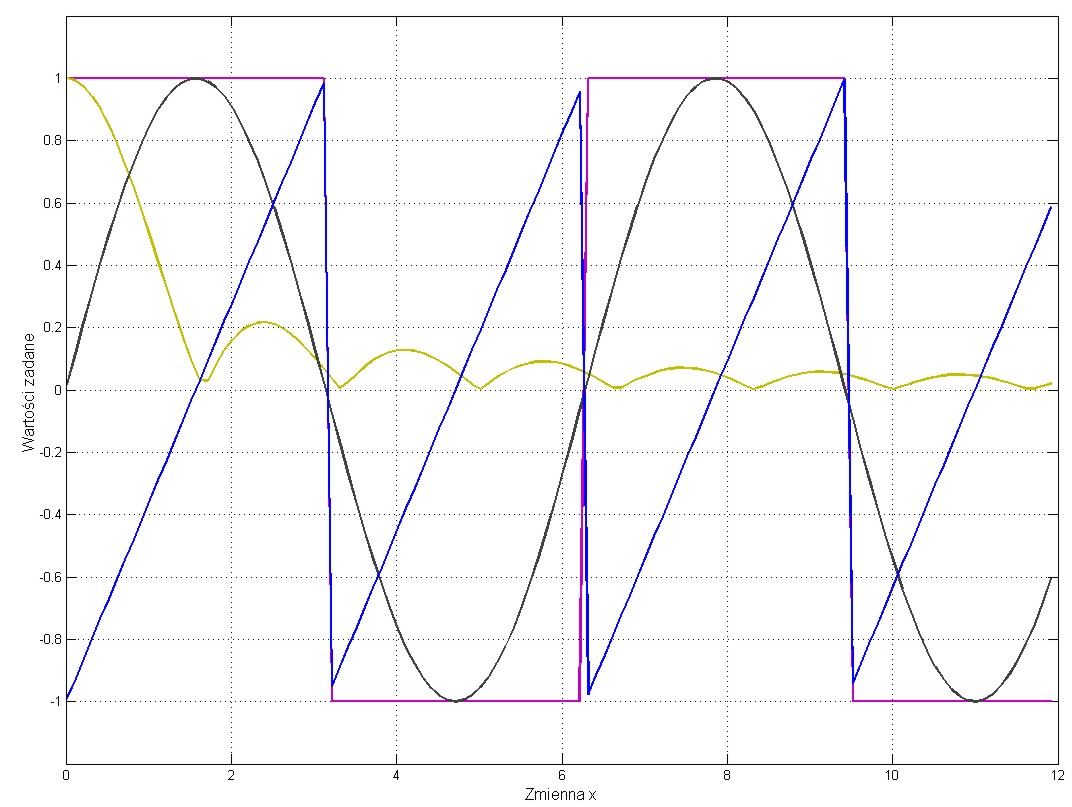
Pierwszym etapem rozwiązania jest generacja danych uczących i testujących (różnych od uczących). Dane testujące wygenerowano dla tych funkcji tablicując ich wartości w punktach \( x \) różnych od tych użytych dla celów uczenia.
Wstępne eksperymenty numeryczne pokazały, że dobre wyniki generalizacji sieci uzyskuje się już przy \( n_h = 20 \) neuronach ukrytych, co oznacza że strukturę sieci można zapisać w postaci 1-20-4. Dane wejściowe stanowią kolejne punkty czasu użytego w generacji danych uczących a wartości zadane wektora czterowymiarowego \( \textbf{d} \) na wyjściu sieci odpowiadają wartościom czterech funkcji poddanych modelowaniu dla zadanych na wejściu punktów czasowych.
Na rys. 2.7 przedstawiono krzywe uczenia sieci aproksymującej przy zastosowaniu różnych algorytmów uczących.
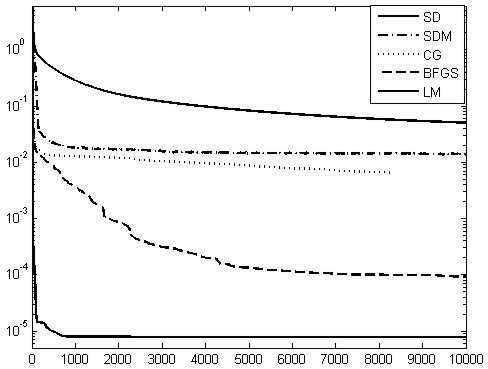
Nie ulega wątpliwości, że najlepszy jest algorytm Levenberga-Marquardta (LM) zarówno pod względem czasu uczenia jak i uzyskanej wartości funkcji celu, a najgorszy algorytm największego spadku (SD). Dla porównania złożoności procesu uczenia przy zastosowaniu różnych algorytmów uczących zaprojektowano dodatkowo sieć przewymiarowaną zawierającą aż \( n_h = 140 \) neuronów ukrytych. Liczba wag sieci optymalnej 1-20-4 jest równa 124, natomiast sieci przewymiarowanej 1-140-4 aż 845.
W tabeli 2.1 przedstawiono (dla porównania skuteczności metod uczenia) liczbę cykli uczących, operacji zmienno-przecinkowych oraz czasy uczenia przy wartości pożądanej funkcji celu równej goal=1e-4 dla obu przyjętych w eksperymencie liczbach neuronów ukrytych 20 oraz 140 (wyniki dotyczą starej wersji Matlaba, w obecnej wersji Matlaba liczba operacji zmiennoprzecinkowych jest niedostępna, a czasy uczenia i liczba cykli uczących zdecydowanie krótsze.
Tabela 2.1 Zestawienie wyników uczenia sieci aproksymującej przy różnej liczbie neuronów ukrytych i różnych metod uczenia
|
Metoda uczenia |
Liczba cykli uczących |
Liczba operacji zmiennoprzecinkowych |
Czas uczenia |
|||
|
\( n_h = 20 \) |
\( n_h = 140 \) |
\( n_h = 20 \) |
\( n_h = 140 \) |
\( n_h = 20 \) |
\( n_h = 140 \) |
|
|
SD |
84785 |
202982 |
1.7e10 |
5.7e10 |
22min 21sek |
51min 28sek |
|
SDM |
10205 |
27822 |
5.2e10 |
6.4e10 |
104sek |
342sek |
|
CG |
226 |
301 |
3.9e8 |
5.4e8 |
20.79sek |
35.5sek |
|
BFGS |
97 |
2094 |
5.9e9 |
5.1e10 |
51.51sek |
342sek |
|
LM |
5 |
43 |
7.9e8 |
7.4e9 |
5.86sek |
67.3sek |
Tym razem wynik oceny jakości algorytmu uczącego w sposób zdecydowany zależy od wielkości sieci. Dla sieci małej najskuteczniejszy pod każdym względem jest znów algorytm Levenberga-Marquardta. W przypadku sieci dużej (845 wag) zdecydowaną przewagę uzyskuje algorytm gradientów sprzężonych (CG) zarówno pod względem czasu uczenia jak i liczby operacji zmienno-przecinkowych.
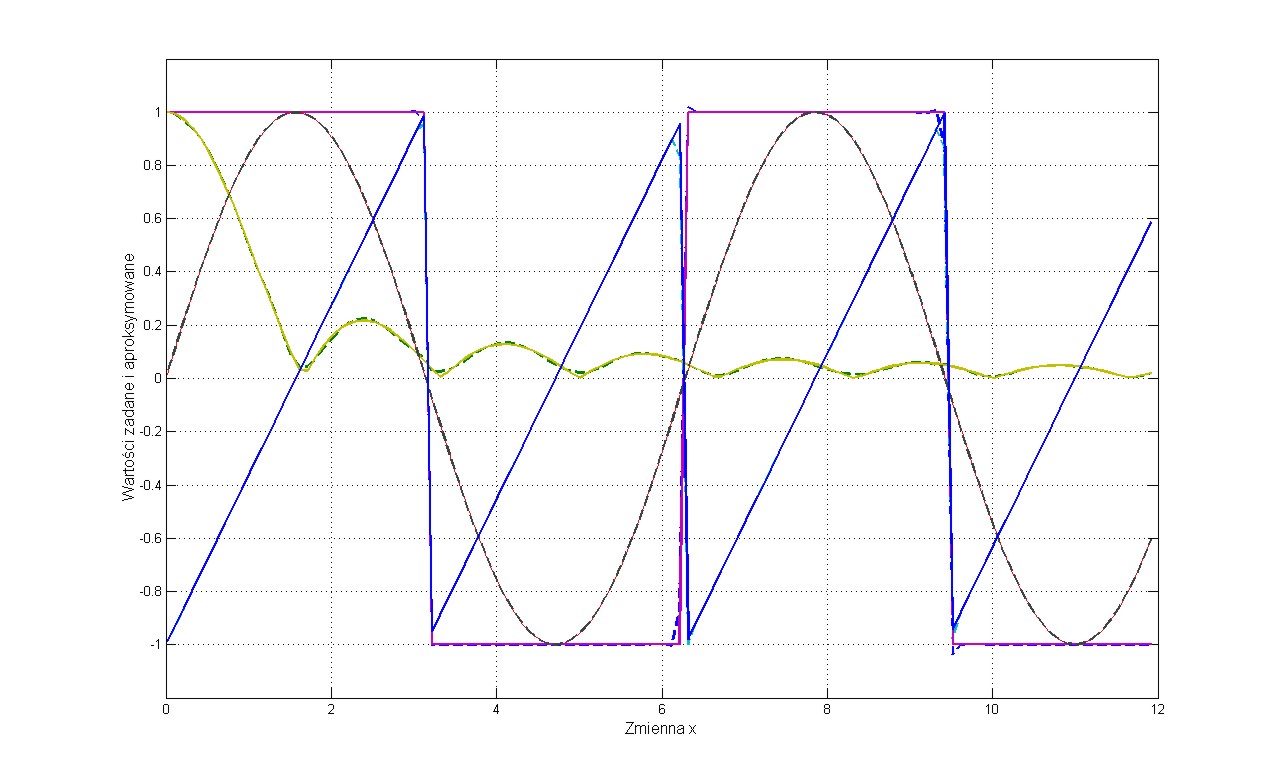
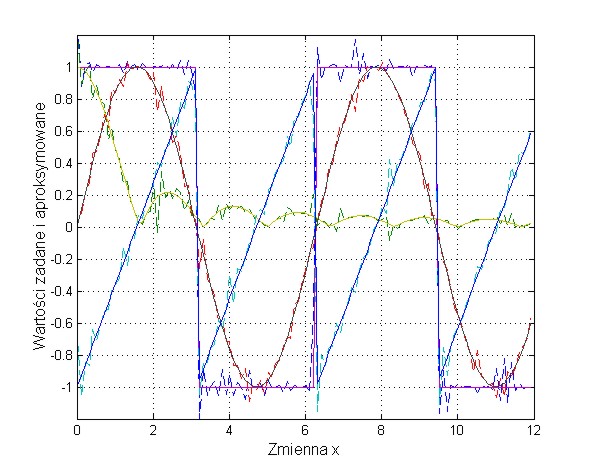
Interesujący jest efekt przewymiarowania sieci neuronowej z punktu widzenia zdolności generalizacyjnych. Zbyt duża sieć neuronowa powoduje utratę tych zdolności w trybie testującym na danych nie uczestniczących w uczeniu. Efekt ten jest przedstawiony na rys. 2.8 (rys. 2.8a - 20 neuronów ukrytych, rys. 2.8b - 140 neuronów ukrytych). Przy 140 neuronach ukrytych krzywe zrekonstruowane przez sieć neuronową charakteryzują się dużymi odkształceniami od przebiegu pożądanego.
Na podstawie wielu przeprowadzonych badań symulacyjnych z użyciem różnorodnych problemów testowych można stwierdzić, że najmniej efektywny jest prosty algorytm największego spadku, szczególnie w przypadku wyboru stałego kroku uczącego. Strategia wyboru metody poszukiwania kierunku minimalizacji \( \textbf{p} \) jest kluczowa dla efektywności algorytmu. Generalnie na podstawie wielu różnych badań testowych można stwierdzić, że algorytmy newtonowskie, w tym metoda zmiennej metryki i Levenberga-Marquardta przewyższają zwykle pod względem efektywności zarówno metodę największego spadku jak i metodę gradientów sprzężonych, ale ta zdecydowana przewaga zanika przy znacznym zwiększeniu rozmiarów sieci. Już przy kilkuset wagach metoda gradientów sprzężonych może górować nad pozostałymi. Metoda największego spadku z momentem rozpędowym jest znacznym udoskonaleniem zwykłej metody największego spadku, choć w badanych przypadkach nieco odbiega od metod newtonowskich. Tym niemniej charakteryzuje się ona dobrą generalizacją, ze względu na możliwość wydostania się z minimum lokalnego dzięki mechanizmowi rozpędu.
2.9.3 Przykład kompresji obrazów przy użyciu sieci MLP
Sieć MLP jest modelem uniwersalnym aproksymatora globalnego. Ma zastosowanie zarówno w zadaniach klasyfikacji (sygnał wyjściowego neuronu sigmoidalnego jest binaryzowany do wartości 1 lub 0 oznaczając przynależność do klasy lub jej brak) jak i regresji (zwykle neurony wyjściowe liniowe). W tym punkcie przedstawimy zastosowanie sieci MLP w problemie kompresji stratnej obrazów (sieć typu regresyjnego). Można przy tym posłużyć się jedną z opcji wyboru w specjalnym programie, którego graficzny interfejs przedstawiony jest na rys. 2.9.
W pierwszym eksperymencie kompresji poddano obraz czarno-biały (obraz oryginalny na rys. 2.10) o wymiarach 64x64 podzielony na ramki o wymiarach 4x4 uzyskując 256 ramek uzytych a w uczeniu. Po zastosowaniu kompresji ze współczynnikiem równym 4 (16 sygnałów wejściowych, 4 neurony ukryte sieci) obraz został zrekonstruowany. Wyniki rekonstrukcji po kompresji i obraz błędnych pikseli (różnica między oryginałem i obrazem odtworzonym) są przedstawione na rys. 2.10. Średni błąd względny odtworzenia jest równy 2.19%.

W drugim eksperymencie kompresji poddano obraz „BOAT” o wymiarze 512x512, podzielony na ramki 8x8 (wymiar ramki 64) uzyskując w sumie 4096 ramek. Przy 8 neuronach ukrytych sieci współczynnik kompresji jest równy 8.

Na rys. 2.11 przedstawiono wyniki graficzne kompresji i rekonstrukcji przedstawiające obraz oryginalny, obraz odtworzony po kompresji (rysunek środkowy) oraz obraz różnicowy (z prawej strony). Tym razem średni błąd odtworzenia jest równy 5.47%.
