Podręcznik

1. Porównać działanie sieci MLP i RBF pod kątem zalet i wad.

2. Korzystając z funkcji pinv Matlaba wyznaczyć pseudoinwersję macierzy losowej \( \mathbf{A} \) (wygenerowanej przy użyciu funkcji rand) przy założeniu, że macierz ta jest kwadratowa oraz prostokątna o liczbie wierszy większej i mniejszej niż liczba kolumn. Sprawdzić za każdym razem iloczyn macierzy \( \mathbf{A}\mathbf{A}^{-1} \). powiązać wyniki z uwarunkowaniem macierzy (funkcja cond Matlaba). Sprawdzić jak wartość funkcji cond zmienia się z wymiarami macierzy \( \mathbf{A} \).

3. Narysować szczegółową strukturę sieci RBF o dwu wejściach, dwu neuronach ukrytych i jednym wyjściu. Utworzyć sieć dołączoną do niej (sposób tworzenia identyczny jak dla sieci MLP przedstawionej w wykładzie 3). Napisać wyrażenia na gradient funkcji celu względem wag liniowych.

4. Rozważyć problem XOR opisany równaniem

Sieć RBF modelująca ten problem zawiera 2 neurony ukryte o centrach \( \mathbf{c}_1 = [1 \;1], \mathbf{c}_2 = [0 \; 0], \sigma_1 = \sigma_2 = 1 \). Określić macierz Greena oraz rozwiązanie względem wag \( \mathbf{w} \) przy wykorzystaniu pseudoinwersji. Wykorzystać odpowiednie funkcje macierzowe Matlaba.

5. Dana jest sieć RBF o strukturze przedstawionej na rys. 4.7

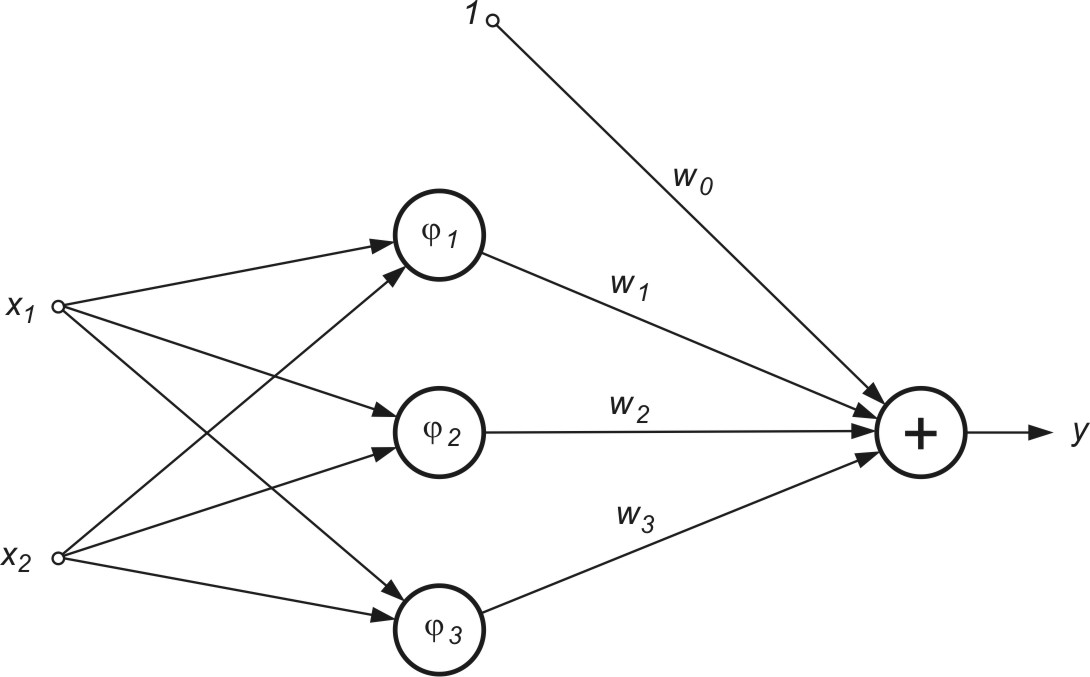
Centra funkcji radialnych dane są w postaci

\( \mathbf{c}_1=\left[\begin{array}{l} 1 \\ 1 \end{array}\right], \quad \mathbf{c}_2=\left[\begin{array}{l} 2 \\ 2 \end{array}\right], \quad \mathbf{c}_3=\left[\begin{array}{l} 3 \\ 0 \end{array}\right] \)

a szerokość wszystkich funkcji równa \( \sigma_1 = 1 \). Wagi sieci są równe: \(w_1 =1, w_2 =0.5, w_3=1.5, w_4=-0.5 \). Sprawdzić przynależność do klasy 1 lub 2 następujących wektorów \( \mathbf{x} \)

\( \mathbf{x}_1=\left[\begin{array}{l} -1 \\ 0 \end{array}\right], \quad \mathbf{x}_2=\left[\begin{array}{l} 2 \\ 1 \end{array}\right], \quad \mathbf{x}_3=\left[\begin{array}{l} 3 \\ 1 \end{array}\right] \)

6. Zaprojektować sieć RBF modelującą funkcję nieliniową dwu zmiennych \( f_1(\mathbf{x})=\sqrt{x_1^2+x_2^2} \) korzystając z programu RBF_win.

7. Wygenerować zbiór danych o rozkładzie losowym typu gaussowskiego o trzech centrach położonych w \( \mathbf{c}_1 = [0.5 \; 1],  \mathbf{c}_2 = [0.3 \;  0.8],  \mathbf{c}_3 = [0.1  \; 0.5] \) (dla każdego centrum po 50 danych). Przyjąć wspólną wartość \( \sigma = 1 \). Napisać program w Matlabie określający centra 5 neuronów ukrytych przy wykorzystaniu metody off-line uczenia ze współzawodnictwem. Zilustrować graficznie otrzymany wynik na tle danych uczących.