Podręcznik
1. Sieci samoorganizujące poprzez współzawodnictwo
1.2. Algorytmy uczące sieci samoorganizujących się przez współzawodnictwo
Celem uczenia sieci samoorganizujących się poprzez współzawodnictwo jest takie uporządkowanie neuronów (dobór wartości ich wag), które zminimalizuje wartość oczekiwaną zniekształcenia (błędu kwantyzacji), określaną jako błąd popełniany przy aproksymacji wektora wejściowego \(\mathbf{x}\) wartościami wag neuronu zwyciężającego w konkurencji. Przy \(p\) wektorach wejściowych \( \mathbf{x} \) i zastosowaniu normy euklidesowej błąd kwantyzacji może być wyrażony w postaci zależności (7.10). Zadanie to zwane jest również kwantyzacją wektorową (ang. Vector Quantization - VQ). Numery neuronów zwyciężających przy kolejnych prezentacjach wektorów x tworzą tak zwaną książkę kodową.
W klasycznym rozwiązaniu kodowania stosuje sią algorytm K-uśrednień (ang. K-means) określany również jako uogólniony algorytm Lloyda [65]. W przypadku sieci neuronowych odpowiednikiem algorytmu Lloyda jest algorytm WTA (ang. Winner Takes All). W algorytmie tym po prezentacji wektora \( \mathbf{x} \) określana jest jego odległość od wektorów wagowych wszystkich neuronów. Zwycięzcą staje się neuron o najmniejszej odległości. Zwycięzca (\(w\)-ty neuron) ma przywilej adaptacji swoich wag w kierunku wektora \( \mathbf{x} \) według reguły [46]
| \( \mathbf{w}_w(k+1)=\mathbf{w}_w(k)+\eta_i(k)\left(\mathbf{x}-\mathbf{w}_w(k)\right) \) | (7.12) |
Pozostałe neurony nie podlegają adaptacji, czyli
| \( \mathbf{w}_i(k+1)=\mathbf{w}_i(k) \) | (7.13) |
Algorytm umożliwia uwzględnienie zmęczenia neuronów poprzez uwzględnienie liczby zwycięstw neuronu i faworyzowanie jednostek o najmniejszej aktywności, dla wyrównania ich szans na zwycięstwo. Modyfikację taką, jak zaznaczono uprzednio, stosuje się głównie w początkowych fazach algorytmu, wyłączając ją po uaktywnieniu wszystkich neuronów. Ostatni sposób uczenia jest zaimplementowany w programie Kohon w postaci opcji CWTA. CWTA pochodzi od angielskiej nazwy algorytmu Conscience Winner Takes All i jest jednym z najlepszych i najszybciej działających algorytmów samoorganizacji.
Oprócz algorytmów WTA, w których tylko jeden neuron może podlegać adaptacji w każdej iteracji, w uczeniu sieci samoorganizujących stosuje się powszechnie algorytmy typu WTM (ang. Winner Takes Most), w których oprócz zwycięzcy uaktualniają swoje wagi również neurony z jego sąsiedztwa, przy czym im dalsza jest odległość neuronu od zwycięzcy, tym mniejsza jest zwykle zmiana wartości wag tego neuronu. Proces adaptacji wektora wagowego może być opisany uogólnioną zależnością [46] z funkcją sąsiedztwa \( G(i, \mathbf{x} ) \) \(i\)-tego neuronu względem wektora wejściowego \( \mathbf{x} \)
| \( \mathbf{w}_i(k+1)=\mathbf{w}_i(k)+\eta_i(k) G(i, \mathbf{x})\left(\mathbf{x}-\mathbf{w}_i(k)\right) \) | (7.14) |
dla wszystkich neuronów \(i\) należących do sąsiedztwa zwycięzcy \(w\). We wzorze tym oddzielono współczynnik uczenia \( \eta \) każdego neuronu od jego odległości względem neuronu zwycięzcy lub od prezentowanego wektora x, mającej wpływ na funkcję sąsiedztwa \(G(i, \mathbf{x})\). Definiując tę funkcję w postaci
| \( G(i, \mathbf{x})=\left\{\begin{array}{llc} 1 & \text { dla } & i=1 \\ 0 & \text { dla } & i \neq w \end{array}\right. \) | (7.15) |
gdzie w oznacza numer zwycięzcy, otrzymuje się klasyczny algorytm WTA. Istnieje wiele różnych odmian algorytmów WTM, różniących się przede wszystkim postacią funkcji \( G(i, \mathbf{x}) \). Przedstawimy tu dwa rozwiązania: algorytm gazu neuronowego oraz algorytm klasyczny Kohonena dostosowany do tworzenia mapy.
7.2.2 Algorytm gazu neuronowego
Znaczącą poprawę samoorganizacji sieci w sensie mniejszego błędu kwantyzacji można uzyskać, stosując metodę zwaną przez autorów algorytmem gazu neuronowego ze względu na podobieństwo dynamiki zmian położenia neuronów do ruchu cząsteczek gazu.
W algorytmie tym wszystkie neurony podlegają sortowaniu w każdej iteracji w zależności od ich odległości ich wektorów wagowych względem wektora x. Neurony są ustawiane w kolejności odpowiadającej narastającej odległości \( d_0 \), gdzie \( d_m=\left\|\mathbf{x}-\mathbf{w}_m\right\| \) oznacza odległość neuronu zajmującego w wyniku sortowania \(m\)-tą pozycję w szeregu za neuronem zwycięzcą, któremu przyporządkowano odległość \( d_0 \). Wartość funkcji sąsiedztwa dla \(i\)-tego neuronu jest określona zależnością [46]
| \( G(i, \mathbf{x})=\exp \left(-\frac{m(i)}{\lambda}\right) \) | (7.16) |
w której zmienna \(m(i)\) oznacza kolejność uzyskaną w wyniku sortowania \( (m(i) = 0,1,\ldots, n-1) \), gdzie 0 oznacza neuron zwycięzcę, a \( \lambda \) jest parametrem (analogicznie do promienia sąsiedztwa w algorytmie Kohonena), malejącym w czasie. Przy \( \lambda=0 \) tylko neuron zwycięzca podlega adaptacji i algorytm WTM przekształca się w zwykły algorytm WTA, natomiast przy \( \lambda > 0 \) adaptacji podlegają wagi wielu neuronów w stopniu uzależnionym od wartości funkcji \(G(i, \mathbf{x})\).
Algorytm gazu neuronowego przypomina strategię zbiorów rozmytych, w której każdemu neuronowi przypisuje się wartość funkcji przynależności do sąsiedztwa, określoną zależnością (7.18). W celu uzyskania dobrych rezultatów samoorganizacji proces uczenia powinien rozpoczynać się z dużą wartością \( \lambda \), po czym powinna ona maleć wraz z upływem czasu do wartości minimalnej (najczęściej zerowej). Zmiana \( \lambda(k) \) może być liniowa bądź wykładnicza. Współczynnik uczenia i-tego neuronu \( \lambda(k) \) może również zmieniać się bądź liniowo bądź wykładniczo. W praktyce lepsze wyniki organizacji uzyskuje się zwykle przy liniowej zmienności \( \lambda(k) \).
Algorytm gazu neuronowego, obok CWTA uwzględniającego aktywność neuronów jest w praktyce najskuteczniejszym narzędziem samoorganizacji neuronów w sieci ze współzawodnictwem. Dobierając odpowiednio parametry sterujące procesem można uzyskać bardzo dobrą organizację sieci przy szybkości działania znacznie przewyższającej klasyczny algorytm Kohonena. Tym nie mniej należy zauważyć, że algorytm ten nie ma zastosowania przy tworzeniu mapy Kohonena, gdyż nie przenosi adaptacji wag na neurony położone w obszarze bliskiego sąsiedztwa (nie zachowuje spójności obszaru aktywności neuronów przy adaptacji).
7.2.3 Algorytmy uczące mapy Kohonena
Algorytm Kohonena należy do najstarszych metod uczenia WTM generujących mapę i w chwili obecnej istnieje wiele jego odmian. W klasycznym algorytmie Kohonena dostosowanym do tworzenia mapy inicjalizuje się sieć, przyporządkowując neuronom określone miejsce w przestrzeni i stowarzyszając je (łącząc) z sąsiadami. Stowarzyszenie to może być interpretowane na siatce prostokątnej (sąsiedztwo prostokątne) lub heksagonalnej (sąsiedztwo heksagonalne). Interpretacja obu rodzajów sąsiedztwa przedstawiona jest na rys. 7.2. Kontury wewnętrzne o kształcie prostokąta lub sześciokąta odpowiadają granicom sąsiedztwa o promieniu odpowiednio zerowym (jedynie zwycięzca – brak sąsiadów), pierwszym, drugim lub trzecim.
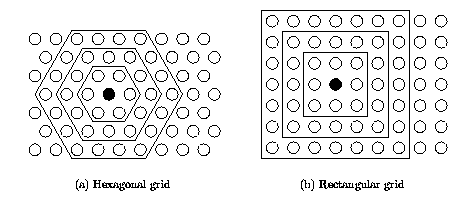
W momencie wyłonienia zwycięzcy uaktualnieniu podlegają nie tylko jego wagi, ale również wagi jego sąsiadów, pozostających w najbliższym sąsiedztwie. W ten sposób adaptacji podlega cała grupa neuronów wokół zwycięzcy zbliżając swoje wagi do prezentowanego wektora x, jak to pokazano w sposób graficzny na rys. 7.3.
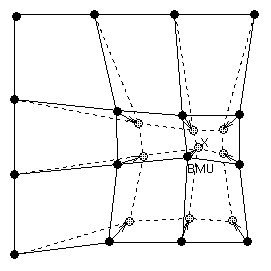
Funkcja sąsiedztwa \(G(i, \mathbf{x})\) w mapie Kohonena może zmieniać się w sposób skokowy (sąsiedztwo prostokątne) lub ciągły. W pierwszym sposobie zwanym przez Kohonena funkcją „bubble” jest ona definiowana w postaci
| \( G(i, \mathbf{x})=\left\{\begin{array}{ccc} 1 & \text { dla } & d(i, w) < \lambda \\ 0 & \text { dla } & \text { reszty } \end{array}\right. \) | (7.17) |
We wzorze tym \(d(i,w)\) może oznaczać bądź odległość euklidesową między wektorami wag zwycięzcy (neuron \(w\)-ty) oraz neuronu \(i\)-tego, bądź odległość mierzoną w liczbie neuronów. Współczynnik \( \lambda \) jest promieniem sąsiedztwa o wartości malejącej, poczynając od zadanej na wstępie wartości maksymalnej aż do zera, przy czym wielkość ta zmienia się w sposób skokowy, wyłączając z sąsiedztwa w kolejnych iteracjach neurony znajdujące się na krańcach obszaru sąsiedztwa. Zauważmy, że tak zdefiniowana funkcja sąsiedztwa \(G(i, \mathbf{x})\) przyjmuje identyczne wartości dla wszystkich neuronów znajdujących się aktualnie w obszarze sąsiedztwa podlegającym adaptacji.
Drugim powszechnie stosowanym typem funkcji sąsiedztwa w mapach Kohonena jest sąsiedztwo typu gaussowskiego, w którym funkcja \(G(i, \mathbf{x})\) określona jest wzorem [46]
| \( G(i, \mathbf{x})=\exp \left(-\frac{d^2(i, w)}{2 \lambda^2}\right) \) | (7.18) |
O stopniu adaptacji neuronów z sąsiedztwa zwycięzcy decyduje nie tylko odległość euklidesowa \(d(i,w)\) neuronu \(i\)-tego od zwycięzcy (neuronu w-tego), ale również promień sąsiedztwa \( \lambda \). W odróżnieniu od sąsiedztwa typu prostokątnego, gdzie każdy neuron należący do sąsiedztwa zwycięzcy podlegał adaptacji w jednakowym stopniu, przy sąsiedztwie typu gaussowskiego stopień adaptacji jest zróżnicowany i zależy od wartości funkcji Gaussa. Dla zwycięzcy obowiązuje \( G(w, w) = 1 \), dla pozostałych neuronów \( 0 < G(i, w) < 1 \). Sąsiedztwo gaussowskie prowadzi zwykle do lepszych rezultatów uczenia i lepszej organizacji sieci niż sąsiedztwo prostokątne.
Istotny wpływ na uczenie sieci Kohonena wywiera dobór wartości współczynnika uczenia \( \eta \) w poszczególnych iteracjach. W ogólności wartość ta powinna maleć w miarę czasu uczenia. Na rys. 7.4 przedstawiono typowe sposoby zmian tego współczynnika.
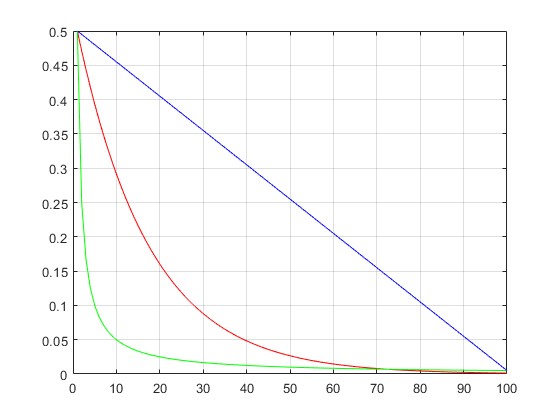
W praktyce najlepsze wyniki samoorganizacji uzyskuje się przy zastosowaniu liniowej formy zmienności współczynnika uczenia.
W mapie Kohonena definiuje się z góry siatkę dwuwymiarową która będzie odzwierciedlała rzut położenia danych wielowymiarowych na płaszczyźnie. Należy z góry określić liczbę neuronów rozmieszczonych w osi poziomej i pionowej. Ogólna liczba neuronów w sieci będzie wówczas równa ich iloczynowi. Neurony te zajmują odpowiednie miejsce w przestrzeni dwuwymiarowej, zachowując powiązanie ze swoimi sąsiadami w procesie uczenia. W efekcie po zakończenia uczenia na etapie testowania zwycięstwo określonego neuronu jest przenoszone na pozycję tego neuronu w siatce dwuwymiarowej (mapie) odzwierciedlając w ten sposób jego rzut na mapę topograficzną. Mapa Kohonena stanowi więc sposób przedstawienia rozkładu danych wielowymiarowych na płaszczyźnie.
Rozkład ten może być przedstawiony na kilka sposobów. Rys. 7.5 przedstawia trzy najczęściej stosowane kształty: mapa płaska, cylindryczna oraz toroidalna. W mapie cylindrycznej dane na dwu przeciwległych krańcach zbliżone są do siebie. W mapie toroidalnej zbliżenie dotyczy dwu przeciwległych krańców w osi x i y.

Dane które w przestrzeni wielowymiarowej są odległe od siebie zajmują również odległe pozycje na mapie. Dane bliskie sobie w przestrzeni wielowymiarowej są również bliskie na mapie.
7.2.4 Przykład mapy Kohonena w analizie obciążeń elektroenergetycznych
Na rys. 7.6 przedstawiono mapę Kohonena o wymiarze 7×7 dla danych dotyczących obciążeń elektroenergetycznych w Polskim Systemie Elektroenergetycznym (PSE). Uwzględniono 12 rodzajów obciążeń odpowiadających 12 miesiącom roku (Jan – styczeń, Feb – luty, Mar – marzec, Apr – kwiecień, May – May, June – czerwiec, July – lipiec, Aug – sierpień, Sep – wrzesień, Oct – październik, Nov – listopad oraz Dec - grudzień). Dane rzeczywiste obciążeń dotyczą wektorów 24-wymiarowych (obciążenia 24 godzin doby). Dzięki mapie Kohonena zostały one zrzutowane na płaszczyznę reprezentując mapę obciążeń odpowiadających poszczególnym miesiącom roku [46].
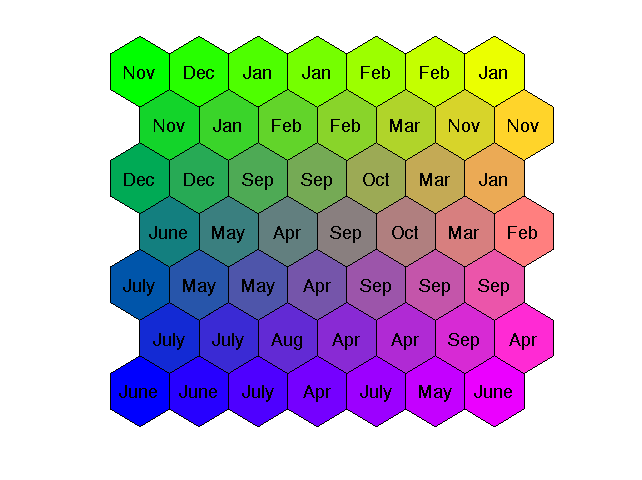
Zauważmy, że dane dotyczące miesięcy letnich i zimowych są odległe od siebie, podczas gdy te związane z wiosną i jesienią są podobne i położone na mapie w bliskim sąsiedztwie. Podobnie można zrzutować obciążenia 24-godzinne na mapę odzwierciedlającą podział na dni tygodnia ( Mon – poniedziałki, Tue – wtorki, Wed – środy, Thu – czwartki, Fri – piątki, Sat – soboty, Sun – niedziele), jak to przedstawiono na rys. 7.7.
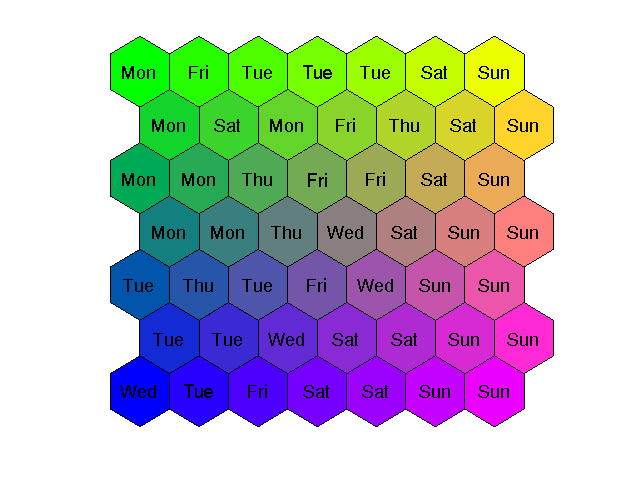
Wyraźnie widoczne są skupienia neuronów reprezentujących dni robocze (od poniedziałku do piątku) oraz oddzielnie świąteczne (Sun). Pomiędzy nimi znajdują się soboty (Sat).
Interesująca jest również mapa profili obciążenia reprezentowana przez wagi neuronów zwycięzców dla poszczególnych rejonów (rys. 7.8). Można zauważyć znaczne podobieństwo miedzy najbliższymi sąsiadami, zarówno w pionie jak i poziomie. Ponadto jest ewidentne, że wagi neuronów odległych od siebie na mapie (np. neurony górne i dolne lub neurony z prawej i lewej strony w tym samym wierszu mapy) są znacznie różniące się.

