Podręcznik: Podstawy matematyczne działania sieci

1. Sieci samoorganizujące poprzez współzawodnictwo

1.1. Podstawy matematyczne działania sieci

Sieci samoorganizujące, dla których podstawą uczenia jest konkurencja między neuronami stanowią zwykle sieci jednowarstwowe, w których każdy neuron połączony jest ze wszystkimi składowymi $N$ -wymiarowego wektora wejściowego $\mathbf{x}$ , jak to przedstawiono schematycznie dla $N = 2$ na rys. 7.1 [46].

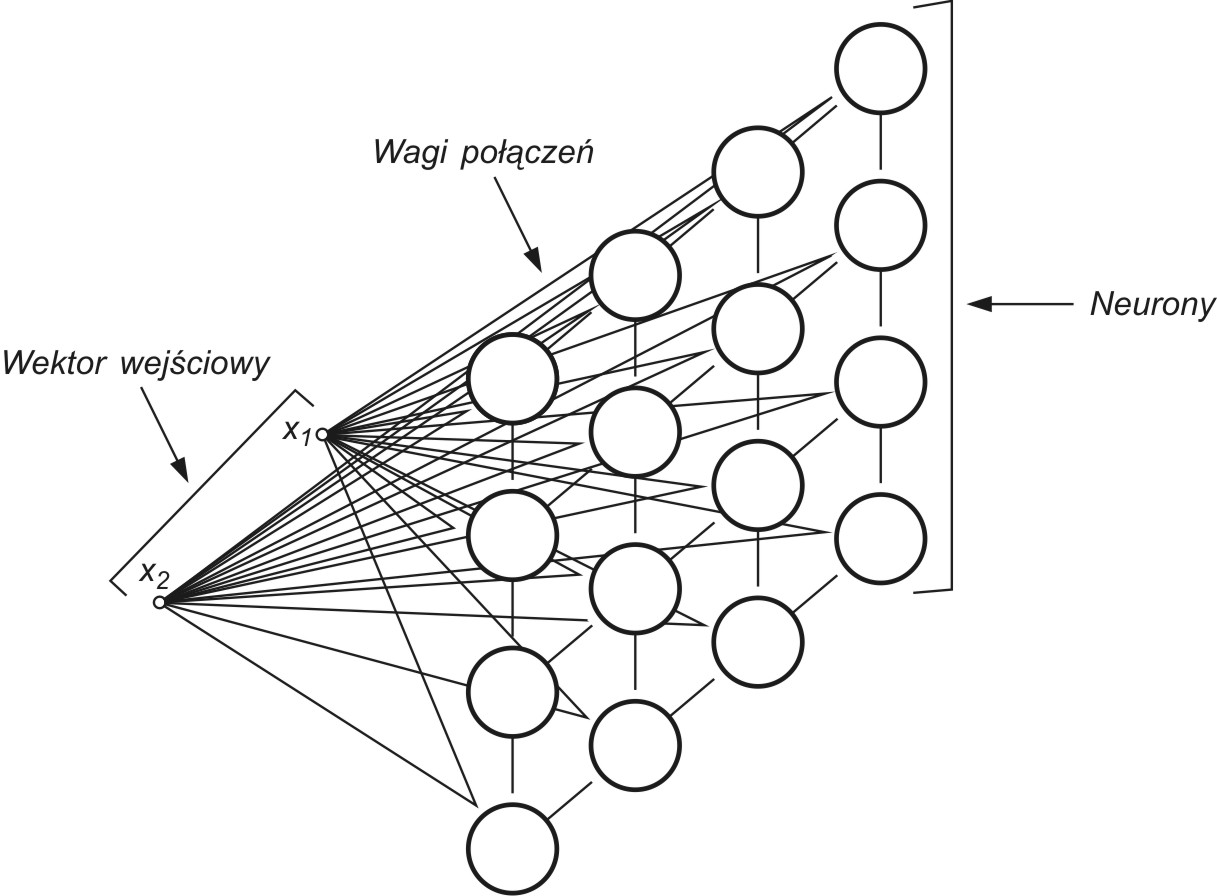
Rys. 7.1 Struktura sieci samoorganizującej Kohonena

Wagi połączeń synaptycznych połączeń $i$ -tego neuronu tworzą wektor $\mathbf{w}_i=[w_{i1}, w_{i2}, …, w_{iN}]^T$ . Przy założeniu normalizacji wektorów wejściowych po pobudzeniu sieci wektorem $\mathbf{x}$ zwycięża we współzawodnictwie neuron, którego wagi najmniej różnią się od odpowiednich składowych tego wektora. Zwycięzca, neuron $w$ -ty, spełnia relację

$d\left(\mathbf{x}, \mathbf{w}_w\right)=\min _{1 \leq i \leq n} d\left(\mathbf{x}, \mathbf{w}_i\right)$

(7.1)

gdzie $d \left(\mathbf{x}, \mathbf{w}_i \right)$ oznacza odległość w sensie wybranej metryki między wektorem x i wektorem w_i, a n jest liczbą neuronów. W uczeniu (adaptacji wag) stosuje się bądź strategię typu Winner Takes All (WTA) lub Winner Takes Most (WTM).

W strategii WTM wokół neuronu zwycięzcy przyjmuje się topologiczne sąsiedztwo S_w(k) o określonym promieniu malejącym w czasie. Neuron zwycięzca i wszystkie neurony położone w obszarze sąsiedztwa podlegają adaptacji, zmieniając swoje wektory wag w kierunku wektora x, zgodnie z regułą Kohonena [46].

$\mathbf{w}_i(k+1)=\mathbf{w}_i(k)+\eta_i(k)\left(\mathbf{x}-\mathbf{w}_i(k)\right)$

(7.2)

w której jest współczynnikiem uczenia i-tego neuronu z sąsiedztwa S_w(k) w k-tej chwili. W regule Kohonena wartość może być taka sama lub różna dla wszystkich neuronów z sąsiedztwa. Wagi neuronów spoza sąsiedztwa S_w(k) nie podlegają zmianom. Rozmiar sąsiedztwa oraz wartości współczynników uczenia poszczególnych neuronów są funkcjami malejącymi w czasie. Zostało wykazane, że przy takim sposobie uczenia funkcja gęstości rozkładu wektorów w_i poszczególnych neuronów jest zbliżona do zdyskretyzowanego rozkładu gęstości wektorów wymuszeń. Po przyłożeniu dwóch różnych wektorów x, np. x₁ i x₂, uaktywnią się dwa neurony sieci, każdy reprezentujący wagi najbliższe współrzędnym wektorów odpowiednio x₁ i x₂. Wagi te oznaczone w postaci wektorowej w₁ i w₂ mogą być zilustrowane w przestrzeni jako dwa punkty. Zbliżenie do siebie wektorów x₁ i x₂ powoduje podobne zmiany położeń wektorów w₁ i w₂. W granicy w₁=w₂ wtedy i tylko wtedy, gdy x₁ i x₂ są sobie równe lub zbliżone do siebie. Sieć spełniająca te warunki nazywa się mapą topograficzną (mapą Kohonena).

Inny sposób uczenia sieci reprezentuje strategia WTA. Zmiana wag zachodzi tu również według zależności (7.2), ale adaptacja dotyczy jedynie neuronu zwycięzcy. Neurony przegrywające konkurencję nie zmieniają swoich wag.

7.1.1 Miary odległości między wektorami

Proces samoorganizacji wymaga na każdym etapie wyłonienia zwycięzcy, czyli neuronu, którego wektor wagowy różni się najmniej od przyłożonego na wejściu sieci wektora x. Istotnym problemem staje się w tej sytuacji wybór metryki, w jakiej mierzona będzie odległość między wektorem x i wektorem w_i. Najczęściej używanymi miarami odległości są [10,16]:

miara euklidesowa

$d_{i j}=\left\|\mathbf{x}_i-\mathbf{x}_j\right\|_2=\sqrt{\left(\mathbf{x}_i-\mathbf{x}_j\right)^T\left(\mathbf{x}_i-\mathbf{x}_j\right)}=\sqrt{\sum_{k=1}^N\left(x_{i k}-x_{j k}\right)}$

(7.3a)

miara Mahalanobisa

$d_{i j}=\sqrt{\left(\mathbf{x}_i-\mathbf{x}_j\right)^T \mathbf{S}^{-1}\left(\mathbf{x}_i-\mathbf{x}_j\right)}$

(7.3b)

gdzie S oznacza macierz kowariancji obu wektorów. W tej definicji wielkości nieskorelowane mają większy wpływ na końcowy wynik niż te, które są mocno lub średnio skorelowane.

iloczyn skalarny

$d\left(\mathbf{x}, \mathbf{w}_i\right)=1-\mathbf{x} \bullet \mathbf{w}_i=1-\|\mathbf{x}\|\left\|\mathbf{w}_i\right\| \cos \left(\mathbf{x}, \mathbf{w}_i\right)$

(7.4)

miara według normy $L_1$ (Manhattan)

$d\left(\mathbf{x}, \mathbf{w}_i\right)=\sum_{j=1}^N\left|x_j-w_{i j}\right|$

(7.5)

miara według normy $L_ \infty$ (Czebyszewa)

$d\left(\mathbf{x}, \mathbf{w}_i\right)=\max _j\left|x_j-w_{i j}\right|$

(7.6)

miara Minkowskiego $L_m$

$d\left(\mathbf{x}, \mathbf{w}_i\right)=\sqrt[m]{\sum_{j=1}^N\left|x_j-w_{i j}\right|^m}$

(7.7)

Przy użyciu miary euklidesowej podział przestrzeni na regiony dominacji neuronów jest równoważny mozaice Voronoia, w której przestrzeń wokół punktów centralnych stanowi strefę dominacji danego neuronu. Zastosowanie innej miary przy samoorganizacji kształtuje podział stref wpływów poszczególnych neuronów nieco inaczej. Szczególnie zastosowanie iloczynu skalarnego bez normalizacji wektorów może prowadzić do niespójnego podziału przestrzeni, przy którym występuje kilka neuronów w jednym regionie, a w innym nie ma żadnego.

7.1.2 Normalizacja wektorów

Wykazano, że proces samoorganizacji prowadzi zawsze do spójnego podziału przestrzeni danych, jeśli wektory $\mathbf{x}$ podlegają normalizacji. Przy znormalizowanych wektorach uczących $\mathbf{x}$ , wektory wag, nadążając za nimi, stają się automatycznie znormalizowane (norma wektora równa 1). Jednakże normalizacja wektora wagowego powoduje, że jeśli $\| \mathbf{x}_i\|=const$ , wtedy dla wszystkich neuronów iloczyn $\| \mathbf{w}_i\| \| \mathbf{x}_i\|$ jest także stały przy określonej wartości $\mathbf{x}$ . O zwycięstwie neuronu decyduje więc wartość kąta między wektorami $\mathbf{x}$ i $\mathbf{w}_i$ zgodnie z zależnością $\cos(\mathbf{x}, \mathbf{w}_i )$ .

Badania eksperymentalne potwierdziły potrzebę stosowania normalizacji wektorów przy małych wymiarach przestrzeni, np. $N=2$ , $N=3$ , natomiast nie jest już tak istotna dla przestrzeni o bardzo dużych wymiarach. Normalizacja wektorów może być dokonana w dwojaki sposób [45]:

redefinicja składowych wektora według wzoru

$x_i \leftarrow \frac{x_i}{\sqrt{\sum_{j=1}^N x_j^2}}$

(7.8)

zwiększenie wymiaru przestrzeni o jeden, przy takim wyborze dodatkowej składowej $(N+1)$ -szej wektora $\mathbf{x}$ , że

$\sum_{j=1}^{N+1} x_j^2=1$

(7.9)

Przy wyborze tego sposobu normalizacji zachodzi zwykle konieczność wcześniejszego przeskalowania składowych wektora $\mathbf{x}$ w przestrzeni $R^N$ w taki sposób, aby możliwe było spełnienie równości (7.9). Przy zwiększaniu wymiaru wektora wejściowego efekt normalizacji staje się coraz mniej widoczny i przy dużych wymiarach sieci, $N > 100$ , normalizacja nie odgrywa większej roli w procesie samoorganizacji.

7.1.3 Problem neuronów martwych

Przy losowej inicjalizacji wag sieci i ograniczeniu wielkości sąsiedztwa neuronów podlegających adaptacji może się zdarzyć, że część neuronów znajdzie się w strefie, w której nie ma danych lub ich liczba jest znikoma. Neurony takie mają niewielkie szanse na zwycięstwo i adaptację swoich wad, pozostając martwymi. W ten sposób dane wejściowe reprezentowane będą przez mniejszą liczbę neuronów (część neuronów martwa), a błąd reprezentacji danych, zwany również błędem kwantyzacji

$\varepsilon=\frac{1}{p} \sqrt{\sum_{i=1}^p\left(\mathbf{x}_i-\mathbf{w}\left(\mathbf{x}_i\right)\right)^2}$

(7.10)

(\ \mathbf{w}(\mathbf{x}_i) \) oznacza wektor wagowy neuronu zwycięzcy dla wektora wejściowego $\mathbf{x}_i$ , natomiast $p$ jest liczbą danych) staje się większy. Istotnym problemem jest zatem uaktywnienie wszystkich neuronów sieci.

Można to osiągnąć, jeśli w algorytmie uczącym będzie uwzględniona liczba zwycięstw poszczególnych neuronów, a proces uczenia zostanie zorganizowany w taki sposób, aby dać szansę zwycięstwa neuronom mniej aktywnym. Sugestia takiej organizacji uczenia bierze się z obserwacji zachowania neuronów biologicznych, gdzie neuron wygrywający tuż po zwycięstwie pauzuje przez określony czas „odpoczywając” przed następnym współzawodnictwem [46]. Taki sposób uwzględniania aktywności neuronów nazywany jest mechanizmem zmęczenia. Oryginalna nazwa conscience mechanism jest w języku polskim określana również mianem mechanizmu świadomości.

Istnieje wiele mechanizmów uwzględniających aktywność neuronów w procesie uczenia. Jednym ze sposobów uaktywnienia wszystkich neuronów jest uwzględnienie liczby zwycięstw neuronu przy obliczaniu efektywnej odległości wag od wzorca uczącego $\mathbf{x}$ , modyfikując ją proporcjonalnie do liczby zwycięstw danego neuronu w przeszłości (na początku wszystkim przypisuje się liczbę zwycięstw równą 1). Jeśli oznaczy się liczbę zwycięstw $i$ -tego neuronu przez $N_i$ , modyfikację taką można przyjąć w postaci

$d\left(\mathbf{x}, \mathbf{w}_w\right) \leftarrow N_i d\left(\mathbf{x}, \mathbf{w}_w\right)$

(7.11)

Neurony aktywne o dużej wartości $N_i$ są karane sztucznym zawyżeniem tej odległości. Należy zaznaczyć, że modyfikację odległości stosuje się jedynie przy wyłanianiu zwycięzcy. W momencie uaktualniania wagi bierze się pod uwagę odległość rzeczywistą. Modyfikacja odległości ma za zadanie uaktywnić wszystkie neurony przez wprowadzenie ich w obszar o dużej liczbie danych. Po wykonaniu zadania (zwykle po dwóch lub trzech cyklach uczących) wyłącza się ją, pozwalając na niezakłóconą konkurencję neuronów [46].