Podręcznik

Przy ocenie jakości sieci neuronowej samoorganizującej ważną rolę odgrywa odwzorowanie danych jedno- i dwuwymiarowych, ze względu na czytelny i przejrzysty sposób interpretacji wyników na płaszczyźnie $x, y$. Biorąc pod uwagę, że wagi neuronów są odpowiednikiem współrzędnych punktów centralnych klastrów, na jakie dzielony jest zbiór danych, można każdemu wektorowi wagowemu przypisać odpowiedni punkt na płaszczyźnie. Łącząc te punkty z najbliższymi sąsiadami otrzymuje się regularną siatkę, odwzorowującą topograficzny rozkład danych (siatka prostokątna lub heksagonalna). Przy równomiernym rozkładzie wektorów uczących $x$ na płaszczyźnie spodziewane odwzorowanie wagowe poszczególnych neuronów przedstawione na płaszczyźnie powinno być równomierne. Jeśli rozkład danych jest nierównomierny, zagęszczenie wystąpi tam, gdzie prawdopodobieństwo wystąpienia wektorów uczących jest większe (patrz rys. 7.14).

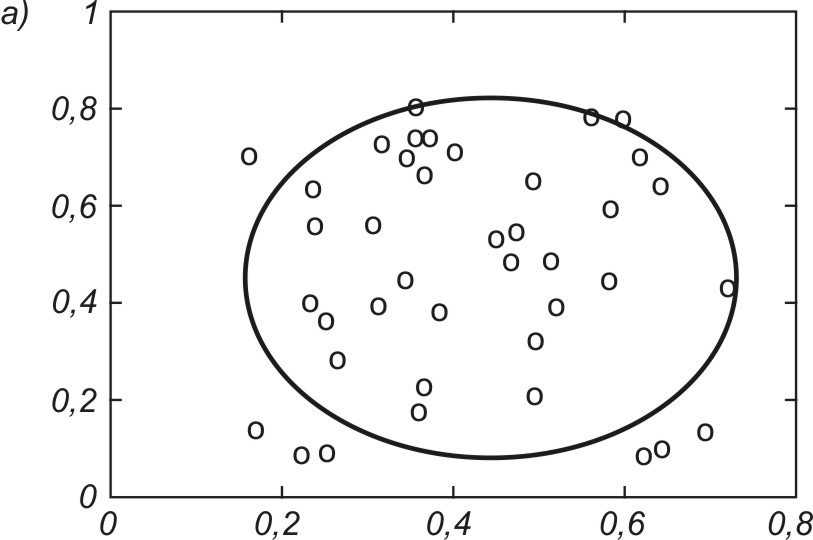
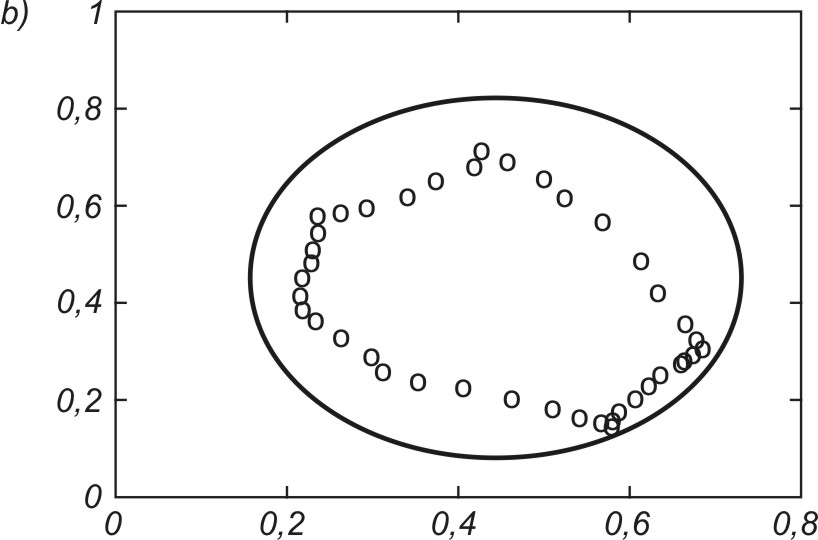
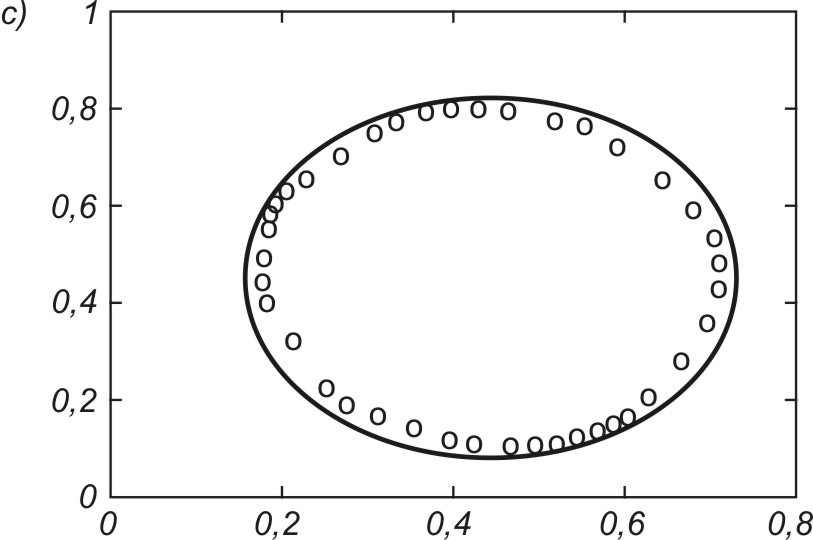
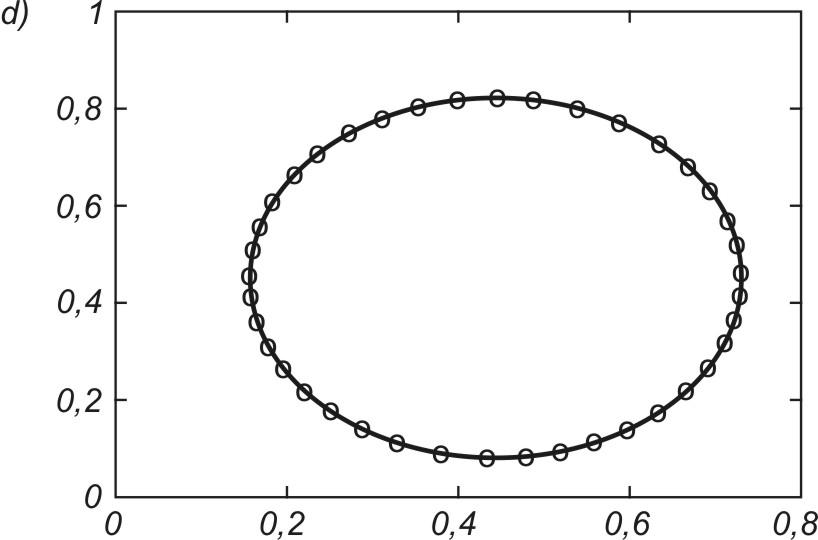
Dobrym testem algorytmów uczących sieci jest odwzorowanie kształtu danych jednowymiarowych za pomocą sieci samoorganizującej. Przykładowo na rys. 7.15 zilustrowano proces samoorganizacji 40 neuronów odwzorowujących układ danych tworzących kształt eliptyczny (pozycje neuronów zaznaczone kółkami). Rys. 7.15a przedstawia stan wyjściowy wag neuronów (rozkład losowy), rys. 7.15b – stan po dwóch cyklach uczących, rys. 7.15c – stan po pięciu cyklach uczących, a rys. 7.15d – stan końcowy (po dziesięciu cyklach) na tle danych uczących tworzących kształt eliptyczny. Uczenie było przeprowadzone przy użyciu programu Kohon i algorytmu gazu neuronowego.

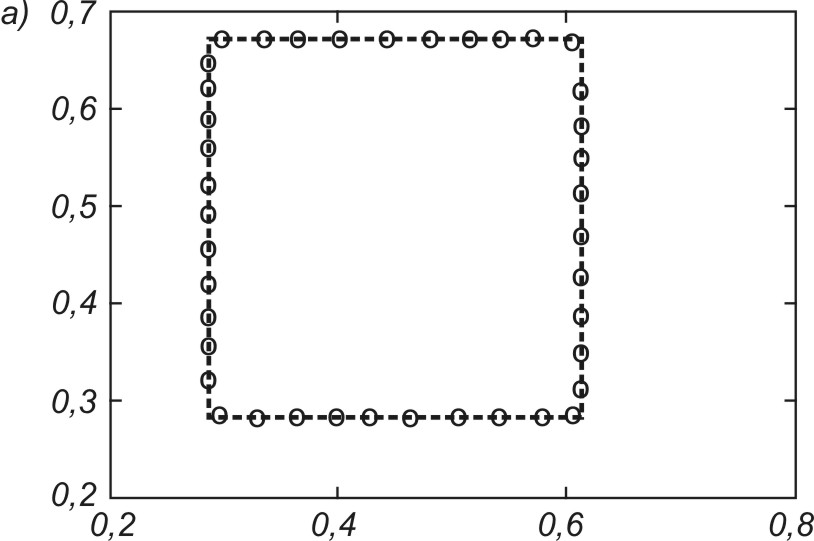
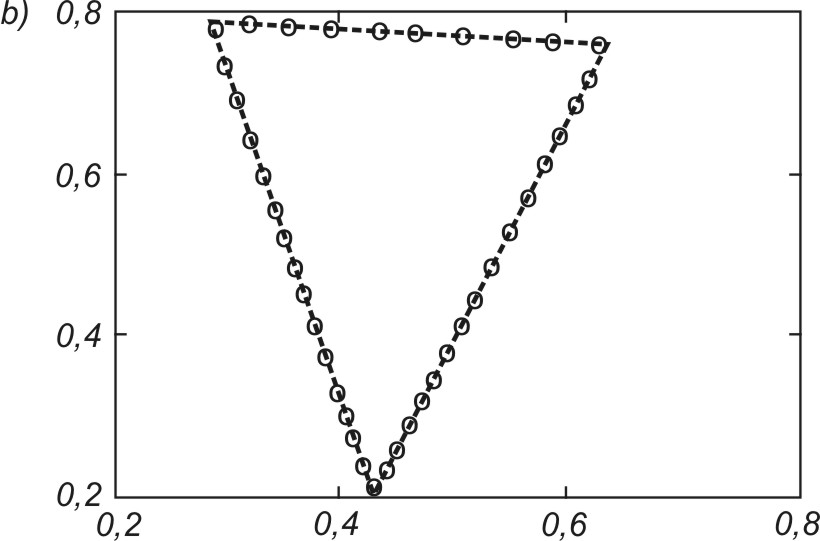
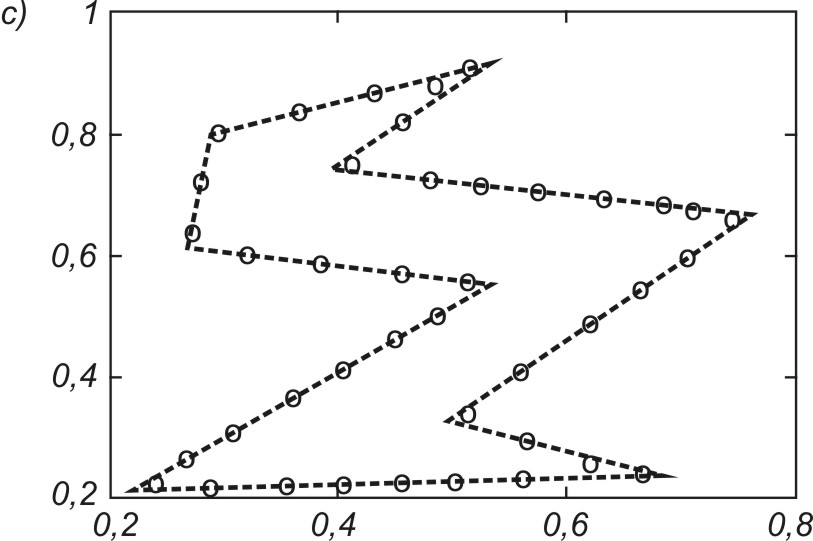
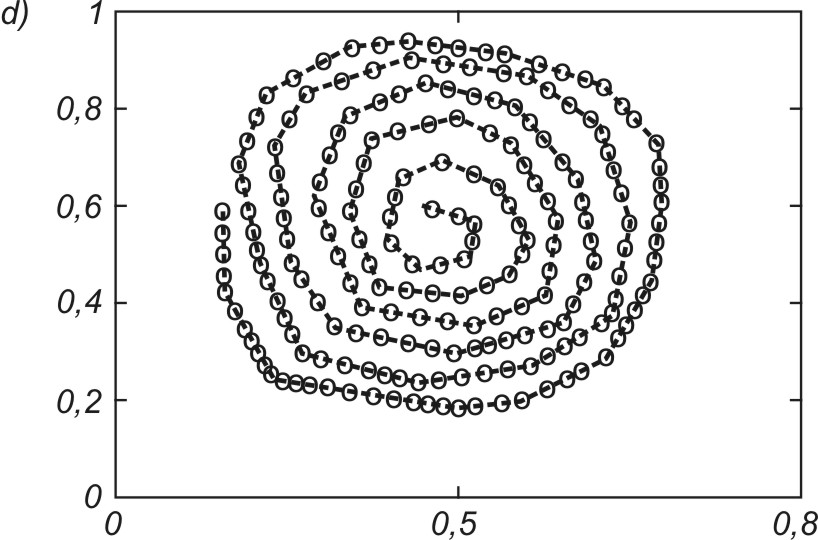
Na rys. 7.16 podano wyniki końcowe uporządkowania neuronów przy odwzorowaniu różnego rodzaju kształtów utworzonych przez dane na płaszczyźnie (x,y). W każdym przypadku wagi neuronów plasują się w strefach występowania danych w taki sposób, aby zminimalizować błąd kwantyzacji. Należy nadmienić, że podstawowa zaleta sieci samoorganizujących się jest widoczna w całej pełni dopiero przy danych wielowymiarowych, gdzie zawodzi zdolność człowieka do wyobrażenia sobie ich rozkładu przestrzennego.

Mechanizmy samoorganizacji wbudowane w algorytmy uczące takich sieci działają niezależnie od wymiarowości problemu. Istotną funkcją pełnioną przez sieć jest tutaj kwantowanie wektorowe, polegające na tym, że ogromna liczba danych tworzących klaster jest odwzorowana przez wektor wagowy jednego neuronu reprezentującego każdy punkt w przestrzeni. Rozkład przestrzenny neuronów pozwala więc określić rozkład skupień danych w przestrzeni wielowymiarowej oraz zasadnicze cechy statystyczne rozkładu danych, przydatne z punktu widzenia użytkownika (centra grup, rozproszenie mierzone wariancją danych w grupie, odległości między centrami różnych grup, itp.)