Podręcznik

Podstawową cechą sieci samoorganizujących się jest kompresja danych, polegająca na tym, że duże grupy danych tworzących klaster reprezentowane są przez pojedynczy wektor wagowy neuronu zwycięzcy. Przy p danych podzielonych na P klastrów i reprezentacji każdego klastra przez jeden z n neuronów uzyskuje się znaczne zmniejszenie ilości informacji, zwane kompresją. Jest to kompresja typu stratnego, której towarzyszy pewien błąd kwantowania określony zależnością (7.10).

Przykładem wykorzystania kompresyjnych własności sieci Kohonena jest kompresja stratna obrazów, mająca za zadanie zmniejszenie ilości informacji reprezentującej dany obraz, przy zachowaniu błędu odwzorowania na określonym poziomie (zapewnienie odpowiednio dużej wartości współczynnika PSNR mierzącego stosunek sygnału do szumu). Zakłada się, że obraz o wymiarach $N_x \times N_y$ pikseli podzielony jest na równomierne ramki zawierające $n_x \times n_y$ pikseli. Piksele każdej ramki stanowią składowe wektorów wejściowych $\mathbf{x}$. Każdy zawiera $n_x n_y$ składników, reprezentujących stopień szarości poszczególnych pikseli w ramce. Przyporządkowanie pikselom wektora może się odbywać przez złączenie poszczególnych wierszy ramki w jeden ciąg bądź przez zastosowanie przyporządkowania typu zygzakowego, stosowanego między innymi w standardzie JPEG.

Sieć samoorganizująca zawiera n neuronów, każdy połączony wagami synaptycznymi ze wszystkimi składnikami wektora wejściowego $\mathbf{x}$. Uczenie sieci przy zastosowaniu jednego z algorytmów samoorganizacji polega na takim doborze wag poszczególnych neuronów, aby zminimalizować błąd kwantyzycji (7.10). W wyniku procesu uczenia następuje taka organizacja sieci, przy której wektorowi $\mathbf{x}$ każdej ramki odpowiada wektor wagowy neuronu zwycięzcy minimalizujący błąd kwantyzacji. Przy podobnym ukształtowaniu składników wektora $\mathbf{x}$ różnych ramek zwyciężać będzie ten sam neuron albo grupa neuronów o podobnych wektorach wagowych. Podczas kolejnej prezentacji ramek ustala się numery neuronu zwycięzcy dla poszczególnych ramek np. 1, 1, 3, 80 itd. Numery neuronów zwycięzców tworzą książkę kodową, a wagi tych neuronów reprezentują uśrednioną wartość odpowiadającą poszczególnym składowym wektora $\mathbf{x}$ (stopień szarości pikseli tworzących ramkę). Wektory te będą przy odtwarzaniu obrazu reprezentować poszczególne ramki. Biorąc pod uwagę, że liczba neuronów $n$ jest zwykle dużo mniejsza od liczby ramek $N_r$, otrzymuje się zmniejszenie ilości informacji przypisanej danemu obrazowi (kompresja).

Przy określaniu stopnia kompresji należy uwzględnić również określoną liczbę bitów użytych do zakodowania numerów neuronów zwycięzców dla poszczególnych ramek. Ostatecznie współczynnik kompresji obrazu definiuje się w postaci [46].

gdzie $n_x$ i $n_y$ oznaczają wymiary ramki w osiach $x , y, N_r$ - liczbę ramek, $n$ - liczbę neuronów, a $T$ i $t$ - liczbę bitów przyjętych w reprezentacji odpowiednio stopnia szarości pikseli i wartości wag. Jakość obrazu odtworzonego charakteryzuje się najczęściej przy użyciu miary PSNR, określonej wzorem

gdzie $MSE$ oznacza wartość błędu średniokwadratowego obrazu odtworzonego względem obrazu oryginalnego. Zastosowanie sieci samoorganizującej do kompresji umożliwia uzyskanie współczynnika kompresji obrazów rzędu nawet 16 przy współczynniku $PSNR$ około 25-28 dB.

Na rys. 7.17a przedstawiono wyniki uczenia sieci Kohonena dla obrazu Barbara o wymiarach $512 \times 512$ pikseli, podzielonego na ramki 16-elementowe (podobrazy o wymiarach $4 \times 4$) [43]. Sieć Kohonena zawierała 512 neuronów. Przy 8-bitowej reprezentacji danych uzyskano stopień kompresji równy: $K_r = 9.9$. Na rys. 7.17b pokazano obraz odtworzony na podstawie wag neuronów zwyciężających przy prezentacji kolejnych ramek. Współczynnik $PSNR$ dla obrazu odtworzonego wynosił 26,2dB. Różnice w jakości obrazu oryginalnego (rys. 7.17a) i odtworzonego (rys. 7.17b) są stosunkowo małe. Widoczne jest to na rys. 7.17c, oddającym obraz błędu, który jest różnicą między obrazem oryginalnym a odtworzonym po kompresji.

  

Ważną zaletą sieci neuronowych, z całą wyrazistością uwidaczniającą się przy kompresji obrazów, jest zdolność generalizacji, a więc możliwość skompresowania (przyporządkowania poszczególnym ramkom nowego obrazu numerów neuronów zwycięzców wytrenowanej wcześniej sieci) i zdekompresowania (przypisania odpowiednich wektorów wagowych zwycięzców poszczególnym ramkom). Jakość odtworzonego obrazu, który nie podlegał wcześniej procesowi uczenia, nie odbiega daleko od jakości obrazu poddanego uczeniu, pod warunkiem, że stopnie zróżnicowania obu obrazów są podobne.

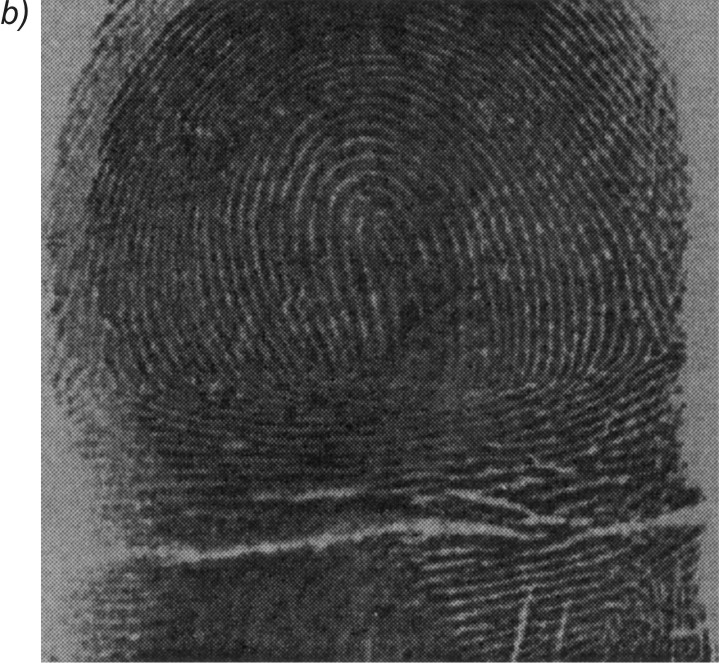
Na rys. 7.18 przedstawiono przykładowy obraz linii papilarnych, poddany procesowi kompresji i dekompresji za pomocą sieci Kohonena, wytrenowanej przy zastosowaniu obrazu z rys. 7.17 [43]. Rysunek 9.18a jest obrazem oryginalnym, rys. 7.18b - obrazem zrekonstruowanym po kompresji, a rys. 7.18c obrazem różnicowym ilustrującym błąd kompresji. Stopień zniekształcenia obrazu odtworzonego jest porównywalny z obrazem poddanym uczeniu, a współczynnik zniekształcenia $PSNR = 26,4 dB$.