Podręcznik
2. Transformacja i sieci neuronowe PCA
2.1. Transformacja PCA
Analiza składników głównych PCA jest metodą statystyczną określającą przekształcenie liniowe \( \mathbf{y} = \mathbf{Wx} \) transformujące opis stacjonarnego procesu stochastycznego dany w postaci zbioru N-wymiarowych wektorów \( \mathbf{x} \) w zbiór wektorów \( \mathbf{y} \) o zredukowanej wymiarowości \( K \le N \) [13,46]. Przekształcenie to odbywa się za pośrednictwem macierzy \( \mathbf{W} \) o wymiarach \( K \times N \) w taki sposób, że przestrzeń wyjściowa o zredukowanym wymiarze zachowuje najważniejsze informacje dotyczące procesu. Innymi słowy, transformacja PCA zamienia dużą ilość informacji zawartej we wzajemnie skorelowanych danych wejściowych w zbiór statystycznie niezależnych składników, według ich ważności. Stanowi zatem formę kompresji stratnej, znanej w teorii komunikacji jako transformacja Karhunena--Loeve.
Dla zachowania maksimum informacji oryginalnej w zbiorze wektorów \( \mathbf{y} \) o zredukowanym wymiarze macierz transformacji \( \mathbf{W} \) powinna być dobrana w taki sposób, aby zmaksymalizować wartość wyznacznika \( J \) [49]
| \( \max _{\mathbf{w}} J=\left|\mathbf{W}^T \mathbf{R}_{xx} \mathbf{W}\right| \) | (8.1) |
W wyrażeniu tym \( \mathbf{R}_{\mathbf{xx}} \) oznacza macierz kowariancji wektorów \( \mathbf{x} \) (przy zerowych wartościach średnich zbioru \( x \) macierz kowariancji jest równa macierzy korelacji). W praktyce centrowanie wektorów nie jest konieczne i można posługiwać się macierzą korelacji, niezależnie od zerowania się wartości średnich. Rozwiązanie powyższego problemu optymalizacyjnego uzyskuje się na podstawie rozkładu macierzy kowariancji zbioru wektorów \( \mathbf{x} \) według wartości własnych.
Przyjmijmy, że \( \mathbf{x} = [x_1, x_2, \ldots, x_N]^T \) oznacza wektor losowy o zerowej wartości średniej, a \( \mathbf{R}_{\mathbf{xx}} = E[\mathbf{xx}]^T \) oznacza wartość oczekiwaną (średnią) macierzy autokorelacji (autokowariancji) po wszystkich wektorach \( \mathbf{x} \). Macierz tę, przy skończonej liczbie \( p \) wektorów \( \mathbf{x} \), można estymować przy pomocy zależności
| \( \mathbf{R}_{\mathbf{xx}}=\frac{1}{p} \sum_{k=1}^p \mathbf{x}^k \mathbf{x}_k^T=\frac{1}{p} \mathbf{X} \mathbf{X}^T \) | (8.2) |
gdzie macierz danych \( \mathbf{X} \) tworzą kolejne wektory uczące \( \mathbf{X} = [\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_p]^T \). Oznaczmy przez \( \lambda_i \) wartości własne macierzy autokorelacji \(\mathbf{R_{xx}} \), a przez \( \mathbf{w}_i \) ortogonalne wektory wartości własnych, skojarzone z nimi, przy czym \( \mathbf{w} = [w_{i1}, w_{i2}, , \ldots, w_{iN}]^T \). Wartości własne oraz wektory własne macierzy \( \mathbf{R_{xx}} \) powiązane są zależnością
| \( \mathbf{R}_{x x} \mathbf{w}_i=\lambda_i \mathbf{w}_i \) | (8.3) |
dla \( i=1, 2, …, N \). Wartości własne symetrycznej, nieujemnie określonej macierzy korelacji \(\mathbf{R_{xx}} \) są rzeczywiste i nieujemne. Uporządkujmy je w kolejności malejącej poczynając od wartości największej \( \lambda_1 > \lambda_2 > \ldots \lambda_N \ge 0 \). W identycznej kolejności ustawimy wektory własne \( \mathbf{w}_i \) skojarzone z odpowiednimi wartościami własnymi \( \lambda_i \). Przy ograniczeniu się do \( K \) największych wartości własnych macierz \( \mathbf{W} \) przekształcenia PCA definiuje się w postaci
| \( \mathbf{W}=\left[\mathbf{w}_1, \mathbf{w}_2, \cdots, \mathbf{w}_K\right]^T \) | (8.4) |
Macierz ta określa transformację PCA jako przekształcenie liniowe
| \( \mathbf{y}=\mathbf{Wx} \) | (8.5) |
Wektor y =[y1, y2,…, yK]T stanowi wektor składników głównych PCA, mających największy wpływ na rekonstrukcję oryginalnego wektora danych x =[x1, x2,…, xN]T. Transformacja PCA jest więc ściśle związana z rozkładem macierzy korelacji według wartości własnych. Uwzględnia zatem jedynie powiązania liniowe między wektorami danych.
Oznaczmy przez \( \mathbf{L} \) macierz diagonalną utworzoną z wartości własnych \( \lambda_i \) uwzględnionych w odwzorowaniu, to jest \( \mathbf{L} = diag\{ {\lambda_1, \lambda_2, \ldots, \lambda_K}\} \). Przy takich oznaczeniach macierz korelacji można przedstawić w postaci zdekomponowanej
| \( \mathbf{R}_{\mathbf{xx}} \cong \mathbf{W}^T \mathbf{L W} \) | (8.6) |
gdzie znak przybliżenia wynika z uwzględnienia skończonej liczby (mniejszej niż wymiar macierzy korelacji) składników głównych. Przy \( K=N \) zależność (8.6) będzie spełniona ze znakiem równości. Uwzględniając symetrię macierzy korelacji zależność tę można jednocześnie przedstawić w postaci
| \( \mathbf{R}_{\mathbf{xx}} \cong \sum_{i=1}^K \lambda_i \mathbf{w}_i \mathbf{w}_i^T \) | (8.7) |
Z punktu widzenia statystycznego transformacja PCA określa zbiór \( K \) wektorów ortogonalnych (kolejne wiersze macierzy \( \mathbf{W} \)), mających największy wkład w wariancję danych wejściowych. Pierwszy składnik główny odpowiadający wektorowi \( \mathbf{x} \) jest równy iloczynowi skalarnemu wektora własnego \( \mathbf{w}_1 \) i wektora wejściowego \( \mathbf{x} \)
| \( y_1=\mathbf{w}_1^T \mathbf{x} \) | (8.8) |
Wektor własny \( \mathbf{w}_1 \) określa zatem kierunek w przestrzeni wielowymiarowej w którym występuje największa wariancja (zmienność wartości) danych wejściowych zawartych w wektorach \( \mathbf{x} \). Wariancja ta jest równa wartości własnej \( \lambda_1 \)
| \( \lambda_1=\operatorname{var}\left(y_1\right)=\operatorname{var}\left(\mathbf{w}_1^T \mathbf{x}\right) \) | (8.9) |
Celem transformacji PCA jest określenie kierunków \( \mathbf{w}_1, \mathbf{w}_2, \ldots, \mathbf{w}_K \) (zwanych kierunkami głównymi) w taki sposób, aby zmaksymalizować wielkość iloczynu skalarnego \( \mathbf{E} (\mathbf{w}_i^T\mathbf{x}) \) dla kolejnych wartości \( i=1, 2, …, K \) przy spełnieniu warunku ortogonalności kolejnych wektorów \( \mathbf{w} \) ze sobą, to jest \( \mathbf{w}_i^T \mathbf{w}_j = 0\) oraz \( \mathbf{w}_i^T \mathbf{w}_i = 1\) .
Rekonstrukcja wektora \( \mathbf{x} \) na podstawie znajomości wektora składników głównych \( \mathbf{y} \) oraz macierzy ortogonalnej \( \mathbf{W} \) przekształcenia PCA odbywa się zgodnie z zależnością [46]
| \( \hat{\mathbf{x}}=\mathbf{W}^T \mathbf{y} \) | (8.10) |
Macierz \( \mathbf{W} \) dekompozycji PCA i macierz rekonstrukcji (\( \mathbf{W}^T \)) stanowią wzajemne transpozycje. PCA minimalizuje wartość oczekiwaną błędu rekonstrukcji danych, przy czym błąd ten określony jest wzorem ogólnym
| \( \varepsilon_r = E[ \| \mathbf{x}-\hat{\mathbf{x}} \| ]^2 \) | (8.11) |
Przy ograniczeniu się do \( K \) największych wartości własnych (\(K\) składników głównych), błąd ten jest proporcjonalny do sumy odrzuconych wartości własnych \( \sum_{i=K+1}^N \lambda_i \).
Ze wzoru tego wynika, że minimalizacja błędu rekonstrukcji danych przy uwzględnieniu \(K\) składników jest równoważna maksymalizacji wariancji rzutowania \( \varepsilon_v \) na etapie rozkładu PCA
| \( \max \varepsilon_v=\sum_{i=1}^K \lambda_i \) | (8.12) |
Zarówno \( \varepsilon_r \), jak i \( \varepsilon_v \) są nieujemne, gdyż wszystkie wartości własne macierzy korelacji, jako macierzy symetrycznej i nieujemnie określonej, są dodatnie bądź zerowe. Wnosimy stąd, że reprezentacja wektora danych \( \mathbf{x} \) przez największe składniki główne \( y_1, y_2, \ldots, y_K \) tworzące wektor \( \mathbf{y} \) jest równoważna zachowaniu informacji o największej porcji energii zawartej w zbiorze danych.
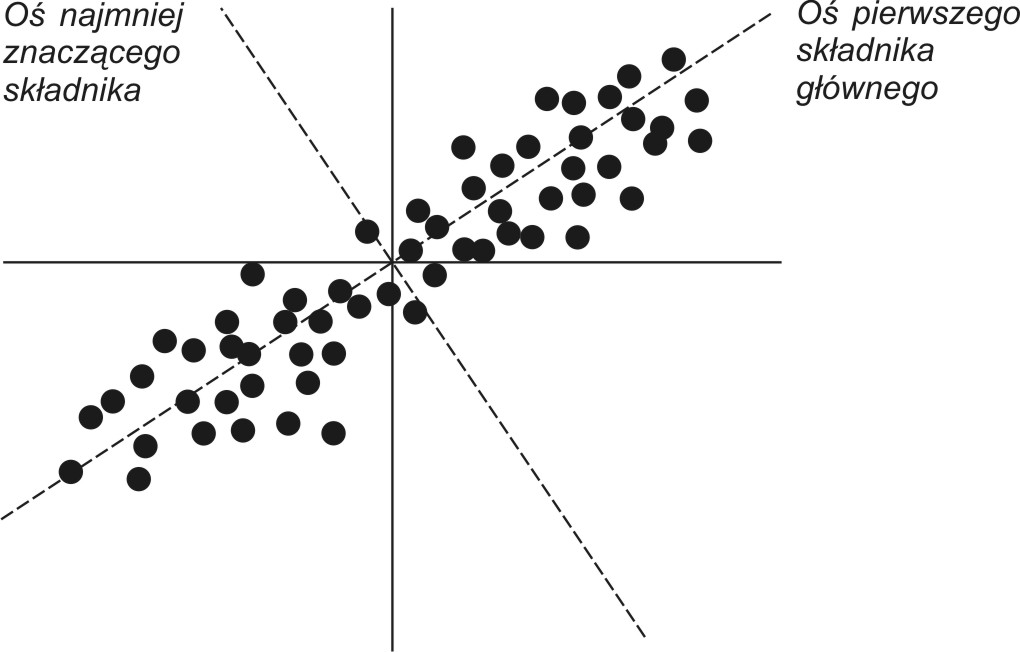
Pierwszy (największy) składnik główny powiązany z \( \lambda_1 \) przez swój wektor własny \( \mathbf{w}_1 \) określa kierunek w przestrzeni wielowymiarowej, w którym wariancja danych jest maksymalna. Ostatni najmniejszy składnik główny (ang. Minor Principal Component) wskazuje kierunek, w którym wariancja jest najmniejsza. Na rys. 8.1 przedstawiono interpretację geometryczną najbardziej znaczącego i najmniej znaczącego składnika głównego transformacji PCA dla danych 2-wymiarowych. Pierwszy składnik główny odpowiada kierunkowi największej zmienności mierzonej poprzez wariancję (energię) sygnałów. Dokonując reprezentacji danych tylko za pomocą jednego składnika głównego oraz skojarzonego z nim wektora własnego i wybierając jako reprezentanta największy ze składników głównych (\(y_1\)), popełnia się najmniejszy błąd rekonstrukcji, maksymalizując jednocześnie wariancję transformacji. Najmniej znaczący składnik główny ma najmniejszy wpływ na dokładność odtworzenia danych. Stąd kompresja danych (zmniejszenie ilości informacji z najmniejszą stratą dla rekonstrukcji) wymaga reprezentowania tych danych przez zbiór największych składników głównych. Pominięcie składników najmniejszych ma najmniej znaczący wpływ na dokładność rekonstrukcji danych.
Transformacja PCA jest ściśle związana z korelacją zachodzącą między wieloma zmiennymi w zbiorze danych. Jeśli te zmienne są skorelowane ze sobą, to znajomość jedynie części z nich wystarczy do określenia pozostałych. Stąd taki zbiór danych może być reprezentowany przez mniejszą liczbę zmiennych. W przypadku gdy nie występuje korelacja między zmiennymi tworzącymi wektor x, predykcja części z nich na podstawie pozostałych jest niemożliwa.
8.1.2 Przykład zastosowania PCA w ekonomii
Jako przykład ilustrujący właściwości rozkładu danych na składniki główne rozpatrzone będą dane GUS-u dotyczące wielkości związanych z miesięcznymi wartościami odpowiadającymi wskaźnikowi cen i usług konsumpcyjnych (wcu), stopie bezrobocia (sb), wartości produkcji sprzedanej w przemyśle (wps) oraz średniej płacy miesięcznej (spm) w Polsce. Przykład ten wykorzystuje dane statystyczne GUS z 10.5 lat (126 wartości).
Wektory pomiarowe x tworzą w tym przypadku cztery składowe, kolejno: wcu, sb, wps oraz spm. Stosując definicję macierzy korelacji (wzór 10.2) w wyniku obliczeń otrzymano macierz korelacji Rxx w postaci
\( \mathbf{R}_{\mathbf{xx}}=10^6\left[\begin{array}{llll}
0.0108 & 0.0017 & 0.0175 & 0.2564 \\
0.0017 & 0.0003 & 0.0027 & 0.0390 \\
0.0175 & 0.0027 & 0.0286 & 0.4226 \\
0.2564 & 0.0390 & 0.4226 & 6.2953
\end{array}\right] \)
Dokonując dekompozycji tej macierzy według wartości własnych uzyskuje się następujące wartości własne (w kolejności malejącej):
\( \lambda_1 = 6334324.26 \)
\( \lambda_2 = 590.69 \)
\( \lambda_3 = 24.10 \)
\( \lambda_4 = 7.48 \)
oraz skojarzone z nimi wektory własne
\( \mathbf{w}_1=\left[\begin{array}{r} 0.0406 \\ 0.0062 \\ 0.0669 \\ 0.9969 \end{array}\right] \), \( \mathbf{w}_2=\left[\begin{array}{r} -0.7609 \\ -0.1859 \\ -0.6173 \\ 0.0736 \end{array}\right] \), \( \mathbf{w}_3=\left[\begin{array}{r} -0.6464 \\ 0.2778 \\ 0.7102 \\ -0.0231 \end{array}\right] \), \( \mathbf{w}_4=\left[\begin{array}{r} -0.0402 \\ -0.9424 \\ 0.3316 \\ -0.0148 \end{array}\right] \)
Na tej podstawie określa się pełną macierz transformacji PCA, zawierającą wszystkie wektory własne ułożone według największego znaczenia (w zależności od wielkości wartości własnych \( \lambda_i \)): \(\mathbf{W}=\left[\mathbf{w}_1, \mathbf{w}_2, \mathbf{w}_3, \mathbf{w}_4\right]^T\) w postaci
\( \mathbf{W}=\left[\begin{array}{rrrr}0.0406 & 0.0062 & 0.0669 & 0.9969 \\ -0.7609 & -0.1859 & -0.6173 & 0.0736 \\ -0.6464 & 0.2778 & 0.7102 & -0.0231 \\ -0.0402 & -0.9424 & 0.3316 & -0.0148\end{array}\right] \)
oraz macierz diagonalną \(\mathbf{L}\) złożoną z wartości własnych macierzy \(\mathbf{R_{xx}} \) ułożonych według malejących wielkości \( \mathbf{L} = diag \{6334324.26, 590.69, 24.10, 7.48 \} \). Największa wartość własna \( \lambda_1 = 6334324.26\) skojarzona jest z pierwszym składnikiem głównym odpowiadającym wektorowi własnemu \( \mathbf{w}_1 \), stanowiącemu pierwszy wiersz macierzy \(\mathbf{W} \). Składnik ten przy wektorze wejściowym \(\mathbf{x} \) złożonym z czterech elementów (\(wcu, sb., wps, spm\)) opisany jest relacją \( y_1 = \mathbf{w}_1^T\mathbf{x}\), która w tym przypadku przybiera konkretną postać: \( y_1 = 0,0406*wcu + 0,0062*sb + 0,0.0669*wps + 0.9969*spm \). Jak widać największy wpływ na składnik główny \( y_1\) ma zmienna \( spm \). Każda z wartości własnych \( \lambda_i \) odpowiada wariancji jaką reprezentuje dany składnik główny. Względny wkład poszczególnych składników głównych w łączną wariancję danych (energię) można określić wzorem:
\(r_i=\frac{\lambda_i}{\sum_{j=1}^4 \lambda_j}\)
Wartości te są następujące: \( r_1 = 0.9999, r_2 = 9,32E-5, r_3 = 3.8E-6, r_4=1.18E-6\). Jak wynika z rozkładu tych wartości, największy składnik główny ma \( 99,99\%\) udziału w łącznej wariancji danych. Przy odtwarzaniu wszystkich składników (\(wcu, sb, wps, spm\)) na podstawie wektora \( \mathbf{y} \) można ograniczyć się jedynie do jego największej składowej \( y_1 \), pomijając pozostałe jako nie wnoszące istotnego wkładu informacyjnego. Oznacza to 3-krotną redukcję ilości przetworzonej informacji. Po odtworzeniu w ten sposób danych uzyskano odtworzony zbiór danych, ze średnim błędem względnym równym \( 0.97\% \) (zdefiniowanym jako stosunek normy euklidesowej macierzy błędu do normy euklidesowej danych przyjętych w postaci macierzy \(4 \times 126\)).
