Podręcznik: Neuronowe metody wyznaczania rozkładu PCA

2. Transformacja i sieci neuronowe PCA

2.2. Neuronowe metody wyznaczania rozkładu PCA

Klasyczna transformacja PCA wymaga wyznaczenia na podstawie danego zbioru wektorów $\mathbf{x}$ najpierw macierzy korelacji $\mathbf{R_{xx}}$ , a następnie rozkładu tej macierzy według wartości własnych. Jest to prosta i łatwa w zastosowaniu metoda (ciąg dekompozycji QR), jeśli problem jest dobrze uwarunkowany (współczynnik uwarunkowania $cond (\mathbf{R_{xx}})$ przyjmuje małe wartości). Wystarczy w tym celu zastosować funkcję eig.m w Matlabie. Przy bardzo dużych wymiarach wektorów x (powyżej kilku tysięcy) problem obliczeniowy wyznaczenia wartości własnych macierzy $\mathbf{R_{xx}}$ staje się zwykle źle uwarunkowany i trudny do przeprowadzenia. W takich przypadkach konkurencyjne może być zastosowanie metod neuronowych adaptacji pozwalających na wyznaczenie macierzy przekształcenia $\mathbf{W}$ bez tworzenia macierzy korelacyjnej, a jedynie poprzez bezpośrednie przetwarzanie wektorów wejściowych $\mathbf{x}$ . Przetwarzanie sygnałów może być wówczas przedstawione w typowo sieciowy sposób jako liniowa sieć PCA zawierająca jedną warstwę.

8.2.1 Estymacja pierwszego składnika głównego

Wyznaczenie wektorów własnych $\mathbf{w_{i}}$ może przebiegać przy zastosowaniu metod adaptacyjnych, typowych dla sieci neuronowych. Są one oparte na uogólnionej regule Hebba i pozwalają na bezpośrednie przetworzenie wektorów wejściowych $\mathbf{x}$ , bez potrzeby jawnego definiowania macierzy $\mathbf{R_{xx}}$ . Metody te są niezastąpione w przypadkach akwizycji danych w trybie on-line, w którym utworzenie jawnej postaci macierzy korelacji byłoby niemożliwe. Powstały różne odmiany algorytmów, a w każdym z nich wykorzystuje się korelację zachodzącą między wektorami reprezentującymi dane wejściowe.

Bezpośrednie zastosowanie uogólnionej reguły Hebba dotyczy wyznaczenia jednego (największego) składnika głównego. Algorytm ten odpowiada zastosowaniu sieci liniowej jednowarstwowej o jednym neuronie wyjściowym przedstawionej na rys. 8.2.

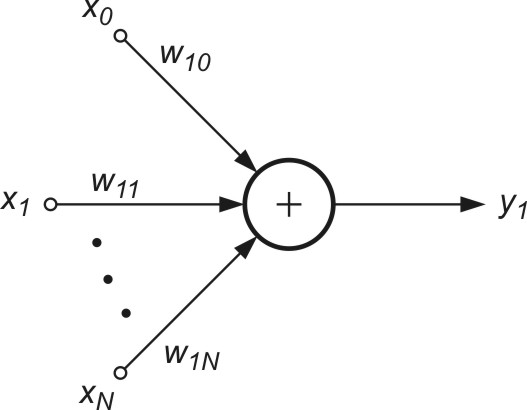
Rys. 8.2 Liniowa sieć PCA do estymacji jednego składnika głównego

Sygnał wyjściowy takiej sieci określony jest wzorem

$y_1=\mathbf{w}_1^T \mathbf{x}=\sum_{j=0}^N w_{1 j} x_j$

(8.13)

Dobór wag wektora $\mathbf{w_{1}}$ odbywa się według uogólnionej (znormalizowanej) reguły Hebba, zwanej regułą Oji, którą zapisać można w formie skalarnej [24,46]

$w_{1 j}(k+1)=w_{1 j}(k)+\eta y_1(k)[ x_j(k)-w_{1 j}(k) y_1(k)]$

(8.14)

lub w formie wektorowej

$\mathbf{w}_1(k+1)=\mathbf{w}_1(k)+\eta y_1(k) [ \mathbf{x}(k)-\mathbf{w}_1(k) y_1(k) ]$

(8.15))

We wzorach tych $\eta$ oznacza współczynnik uczenia malejący w czasie. W procesie uczenia sieci powtarza się wielokrotnie te same wzorce uczące, aż do ustabilizowania się wag sieci. Pierwszy składnik obu wzorów odpowiada zwykłej regule Hebba, a drugi zapewnia samo-normalizację wektorów wagowych, to jest $\| \mathbf{w}_1\|^2=1$ . Dobór wartości $\eta$ ma istotny wpływ na zbieżność algorytmu. Dobre rezultaty uzyskuje się, przyjmując wartości $\eta(k)$ malejące wraz z upływem czasu uczenia.

Jakkolwiek metoda Oji pozwala wyznaczyć jedynie pierwszy składnik główny może być ona w prosty sposób przystosowana do wyznaczenia pozostałych składników. Przy uwzględnieniu wielu składników i wektorów własnych można sukcesywnie redukować wpływ wyselekcjonowanego składnika pierwszego odkrywając w ten sposób następny, traktowany w przekształconym wektorze $\mathbf{x}$ jako pierwszy składnik główny, dla którego można powtórzyć poprzednia procedurę. Przyjmując oznaczenie $i$ -tego wektora własnego w postaci $\mathbf{w_{i1}} = [w_{i1}, w_{i2}, \ldots, w_{iN}]^T$ można zauważyć, że składowe wektora $\mathbf{x}$ można wyrazić w postaci

$x_i=w_{i 1} x_1+\sum_{j=2}^K w_{i j} y_j$

(8.16)

dla $i=1, 2, \ldots, N$ . Składnik pierwszy tego wzoru po wyznaczeniu pierwszego składnika głównego jest już znany i może zostać wyeliminowany poprzez utworzenie nowego wektora $\mathbf{x}^\prime$ o elementach zdefiniowanych następująco

$x_i^{\prime}=x_i-w_{i 1} x_1$

(8.17)

Dla nowego wektora $x_i^{\prime}$ największą wartością własną jest teraz $\lambda_2$ , gdyż wpływ $\lambda_1$ został wyeliminowany dzięki działaniu wyrażonemu wzorem (8.17). Procedura wyznaczenia tej wartości jest identyczna do omówionej wcześniej. Powtarzając te operacje $N$ razy można wyznaczyć wszystkie wektory własne stowarzyszone z kolejnymi wartościami własnymi.

8.2.2 Algorytm estymacji wielu składników głównych jednocześnie

Wyznaczanie wielu kolejnych składników PCA wymaga zastosowania wielu neuronów w warstwie wyjściowej sieci. Sieć neuronowa zawiera zatem tyle neuronów, ile składników głównych rozkładu ma być uwzględnionych. Są one ułożone w jednej warstwie - stąd sieć PCA jest siecią jednowarstwową o liniowych funkcjach aktywacji neuronów (rys. 8.3).

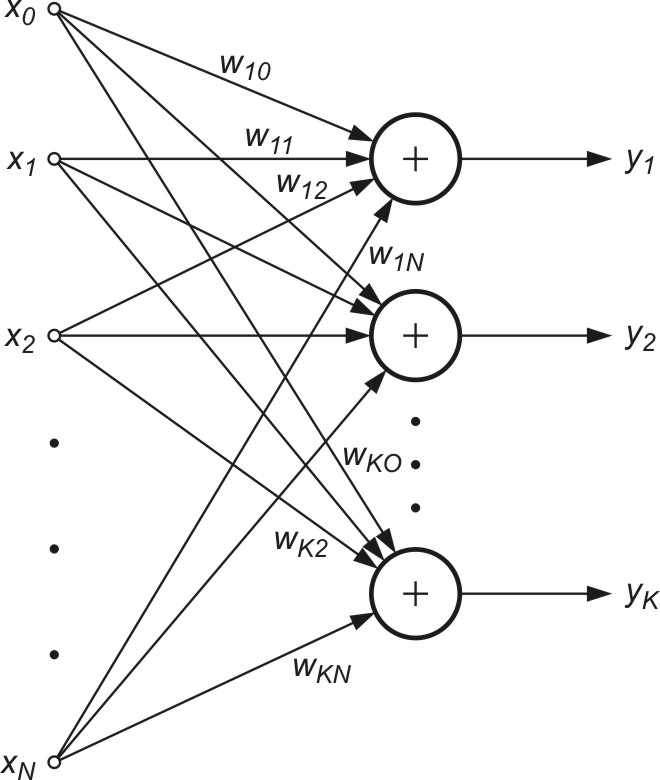
Rys. 8.3 Sieć neuronowa liniowa PCA do estymacji

$K$ składników głównych na raz

Istnieje wiele algorytmów uczenia takiej sieci. Tutaj ograniczymy się do reguły Sangera [24,46], będącej regułą lokalną, nie wymagającą w procesie uczenia rozwiązania układu równań. Przy $K$ neuronach liniowych w warstwie sygnały wyjściowe $y_i$ w kolejnych iteracjach $k$ określane są według wzoru

$y_i(k)=\mathbf{w}_i^T(k) \mathbf{x}(k)=\sum_{j=1}^N w_{i j} x_j$

(8.18)

Adaptacja wag sieci w kolejnych iteracjach wykorzystuje aktualnie znane (zaadaptowane) wartości wag i przebiega według następującego wzoru

$w_{i j}(k+1)=w_{i j}(k)+\eta y_i(k)\left[x_j(k)-\sum_{h=1}^i y_h(k) w_{h j}(k)\right]$

(8.19)

dla $j=1, 2, …, N$ oraz $i=1, 2, …, K$ . Przyjmując oznaczenie

$x_j^{\prime}(k)=x_j(k)-\sum_{h=1}^{i-1} w_{h j}(k) y_h(k)$

(8.20)

zależność (8.19) można przedstawić w postaci analogicznej do reguły Oji przy jednym neuronie wyjściowym

$w_{i j}(k+1)=w_{i j}(k)+\eta y_i(k)\left[x_j^{\prime}(k)-y_i(k) w_{i j}(k)\right]$

(8.21)

Jest oczywiste, że nawet przy istnieniu $K$ neuronów w warstwie wyjściowej reguła uczenia pozostaje nadal lokalną, pod warunkiem zmodyfikowania wartości sygnału wejściowego $x_j^\prime$ . Zauważmy, że modyfikacja tego sygnału odbywa się przy wykorzystaniu wcześniej zaadaptowanych już wartości wag, a więc nie wymaga rozwiązania układu równań. Zależności skalarne (8.20) i (8.21) można zapisać w prostszej formie wektorowej wygodniejszej w działaniach

$\mathbf{x}^{\prime}(k)=\mathbf{x}(k)-\sum_{h=1}^{i-1} y_h(k) \mathbf{w}_h(k)$

(8.22)

$\mathbf{w}_i(k+1)=\mathbf{w}_i(k)+\eta y_i(k)\left[\mathbf{x}^{\prime}(k)-y_i(k) \mathbf{w}_i(k)\right]$

(8.23)

dla $i=1, 2,…, K$ . Zauważmy, że dla neuronu pierwszego (pierwszy składnik główny PCA) mamy $\mathbf{x}^{\prime}(k)=\mathbf{x}(k)$ . Dla neuronu drugiego otrzymuje się $\mathbf{x}^{\prime}(k)=\mathbf{x}(k)-\mathbf{w}_1(k) y_1(k)$ - wzór uzależniony od znanych już wag neuronu pierwszego. Podobnie dla trzeciego neuronu $\mathbf{x}^{\prime}(k)=\mathbf{x}(k)-\mathbf{w}_1(k) y_1(k)-\mathbf{w}_2(k) y_2(k)$ i wszystkich pozostałych, modyfikacja wektora $\mathbf{x}$ wyrażona jest przez wielkości wag wcześniej określone, w efekcie czego proces uczenia przebiega identycznie jak w przypadku algorytmu Oji, z samo-normalizującymi się wektorami $\mathbf{x}$ , czyli $\left\|\mathbf{w}_i\right\|=1$ .

Obecnie istnieje wiele różnych algorytmów neuronowych, pozwalających adaptacyjnie określić parametry transformacji PCA. Do najważniejszych, oprócz algorytmu Sangera, zalicza się algorytm Foldiaka, Rubnera oraz APEX (ang. Adaptive Principal component EXtraction). Szczegóły rozwiązań znaleźć można w opracowaniu książkowym Diamantarosa i Kunga.