Podręcznik

Główne zastosowania transformacji PCA związane są z kompresją danych, która jest nieodłącznym składnikiem każdego przekształcenia PCA. Własność ta może być bezpośrednio wykorzystana do kompresji stratnej informacji – mówimy wtedy o kompresji sygnałów (dane jednowymiarowe) bądź obrazów (dane 2-D). Niezastąpionym zastosowaniem PCA jest ilustracja rozkładu danych wielowymiarowych na płaszczyźnie (układ 2-współrzędnych w postaci 2 najważniejszych składników głównych) lub w przestrzeni 3-D (układ 3-współrzędnych w postaci 3 najważniejszych składników głównych). Ponadto transformacja PCA reprezentująca $N$-wymiarowy wektor $\mathbf{x}$ przez $K$-wymiarowy ($K$) wektor $\mathbf{y}$ składników głównych pozwala traktować wektor $\mathbf{y}$ jako wektor cech diagnostycznych procesu reprezentowanego przez zbiór wektorów $\mathbf{x}$.

8.3.1 PCA w zastosowaniu do kompresji stratnej danych

Kompresja danych z zastosowaniem PCA polega na przekształceniu $N$-elementowego wektora wejściowego $\mathbf{x}$ w wektor $\mathbf{y}$ o zmniejszonym wymiarze $K$ ($K$). Redukcja wymiaru wektora $\mathbf{x}$ poprzez PCA zapewnia optymalność przekształcenia poprzez zachowanie w wektorze zredukowanym największej możliwie dawki informacji oryginalnej (przy założonej wartości $K$).

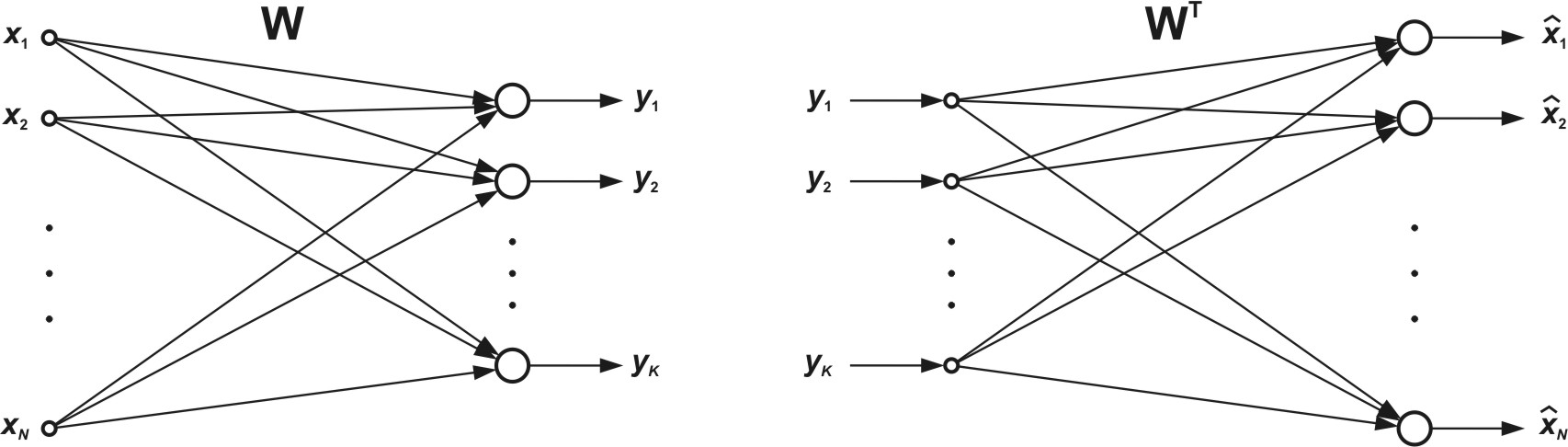
Na rys. 8.4 przedstawiono sieć PCA do kompresji (rys. 8.4a) oraz do rekonstrukcji (dekompresji) danych (rys. 8.4b). W sieci kompresyjnej wektor oryginalny $\mathbf{x}$ jest transformowany w wektor $\mathbf{y}$ o zredukowanym wymiarze $K$, przy czym $\mathbf{y} = \mathbf{Wx}$. Wektor $\mathbf{y}$ może podlegać bądź to transmisji na odległość bądź zapisaniu na dysku. W każdym przypadku możliwe jest odtworzenie wektora oryginalnego na podstawie jego zredukowanej formy $\mathbf{y}$, korzystając z sieci rekonstrukcyjnej z rys. 8.4b, wykonującej operację odwrotną $\mathbf{\hat{y}} = \mathbf{W^Tx}$. Biorąc pod uwagę pewną utratę informacji spowodowaną obcięciem wymiaru wektora odtworzenie to jest z pewnym przybliżeniem $\hat{\mathbf{x}} \simeq \mathbf{x}$.

O współczynniku kompresji decyduje liczba składników głównych $K$ uwzględnionych w przekształceniu PCA. Przy dużej liczbie wektorów $\mathbf{x}$ podlegających przekształceniu można pominąć liczbę bitów do kodowania wag sieci i współczynnik kompresji wyrazić wzorem przybliżonym

Im wyższy współczynnik kompresji tym większa oszczędność pamięci, ale gorsza jakość odtworzonego obrazu (większa porcja informacji utracona bezpowrotnie w wyniku redukcji wymiaru wektora oryginalnego).

Na rys. 8.5 przedstawiono obraz oryginalny (rys. 8.5a) oraz trzy obrazy zrekonstruowane na podstawie odpowiednio 1, 3 i 5 składników głównych PCA (rys. 8.5 b,c,d). Obraz poddany kompresji miał wymiar $512 \times 512$ pikseli i został podzielony na ramki o wymiarach $8 \times 8$ (wymiar wektora $\mathbf{x}$ równy $64$). Jakość odtworzonego obrazu jest ściśle uzależniona od liczby $K$ składników głównych uwzględnionych w odtwarzaniu. Im więcej jest tych składników, tym lepsza jakość obrazu, ale mniejszy współczynnik kompresji. Przy największym współczynniku kompresji (jeden składnik główny) wyraźnie widoczne są poszczególne ramki w obrazie. Obraz odtworzony na podstawie pięciu składników głównych nie różni się wzrokowo od obrazu oryginalnego. Współczynniki PSNR otrzymane dla poszczególnych obrazów są odpowiednio równe: 18,80 dB, 25,43 dB oraz 27,58 dB, przy czym $\mathbf{PSNR}$ określany jest wzorem

gdzie $MSE$ oznacza wartość błędu średniokwadratowego odtworzonego obrazu względem obrazu oryginalnego.

8.3.2 Przykład zastosowania PCA do ilustracji rozkładu danych wielowymiarowych

Oryginalne zastosowanie znalazło PCA w ilustracji graficznej rozkładu danych wielowymiarowych poprzez zrzutowanie ich w przestrzeń 2-D lub 3-D. Wybierając $K=2$ rzutujemy każdy $N$-wymiarowy wektor $\mathbf{x}$ w przestrzeń dwuwymiarową. W ten sposób każdy wektor $\mathbf{x}$ jest reprezentowany przez wektor $\mathbf{y} = [y_1 y_2]$, którego położenie może być bez problemu zilustrowane na płaszczyźnie, której oś poziomą stanowi teraz składnik główny $y_1$, a oś pionową składnik główny $y_2$. Wektory $\mathbf{x}$ „podobne” do siebie zajmą wówczas bliskie sobie położenia na płaszczyźnie, a wektory „dalekie” – położenia odległe.

Ta unikalna własność znajduje szerokie zastosowania w problemach klasyfikacyjnych, gdzie służy do badania jednorodności rozkładów danych w ramach poszczególnych klas oraz do określania średnich odległości między klasowych

Przykład takiego zastosowania pokażemy w przestrzeni 2-wymiarowej ilustrującej graficznie położenie poszczególnych województw Polski (na płaszczyźnie reprezentowanej przez 2 najważniejsze składniki główne). Wyniki dotyczą przykładowych danych GUS z jednego roku. Rzutowanie dotyczyło 13-wymiarowych elementów informacji GUS dla każdego województwa. Informacje dotyczą następujących elementów:

1. Procent ludności mieszkających w miastach

2. Odsetek zgonu niemowląt

3. Przyrost naturalny ludności

4. Stopa bezrobocia

5. Wynagrodzenie miesięczne brutto

6. Zasoby mieszkaniowe przypadające na 10000 ludności

7. Liczba osób hospitalizowanych w roku przypadających na 10000 ludności

8. Liczba ciągników rolniczych przypadająca na 100 ha gruntów

9. Produkcja sprzedana przemysłu przypadająca na głowę ludności

10. Produkcja sprzedana budownictwa przypadająca na głowę ludności

11. Liczba kilometrów dróg przypadających na 10km2 w przeliczeniu na głowę ludnosci

12. Wartość PKB per capita

13. Liczba firm zarejestrowanych w bazie REGON przypadająca na głowę ludności

Dla uproszczenia opisów przyjęto numeryczne oznaczenia poszczególnych województw w kolejności jak niżej:

1. Dolnośląskie

2. Kujawsko-pomorskie

3. Lubelskie

4. Lubuskie

5. Łódzkie

6. Małopolskie

7. Mazowieckie

8. Opolskie

9. Podkarpackie

10. Podlaskie

11. Pomorskie

12. Śląskie

13. Świętokrzyskie

14. Warmińsko-mazurskie

15. Wielkopolskie

16. Zachodniopomorskie

Tabela 8.1 przedstawia dane oryginalne dotyczące tych zagadnień. Wektor x dla każdego województwa tworzy wybranych 13 elementów informacji dotyczącej ekonomii, dostępności edukacji i opieki medycznej. Użyto następujących skrótów:

Tabela 8.1 Dane liczbowe GUS dotyczące 13 elementów informacji województw w Polsce. Wiersze reprezentują województwa (od 1 do 16), kolumny elementy uwzględnionej informacji (od 1 do 13)

Na rys. 8.6 przedstawiono ilustrację dwuwymiarową położenia względnego 16 województw Polski na podstawie danych statystycznych dotyczących rozwoju ekonomicznego, stanu edukacyjnego i opieki medycznej.

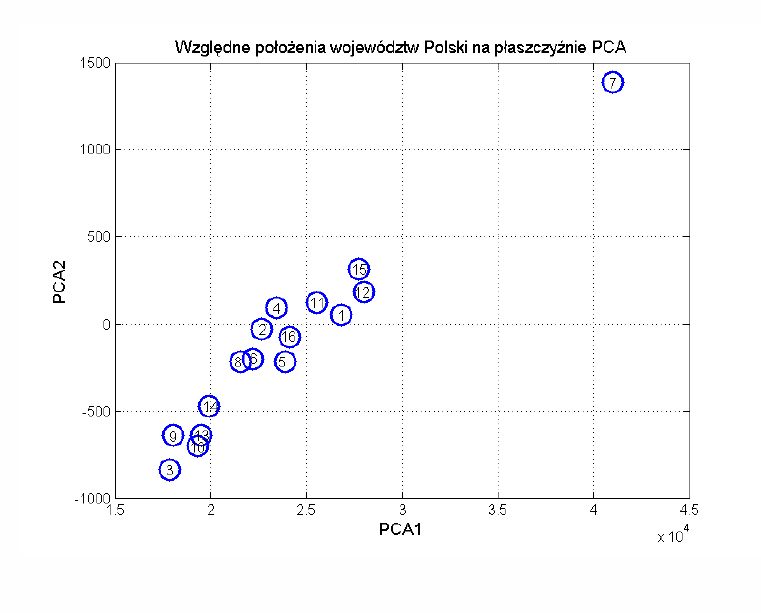
Bliskie położenie na płaszczyźnie oznacza podobieństwo cech charakteryzujących te województwa. Większe odległości miedzy poszczególnymi punktami oznaczają większe różnice w rozwoju tych województw (pod względem uwzględnionych 13 wskaźników ekonomicznych i społecznych). Najbardziej odstającym województwem, wyróżniającym się w grupie analizowanych jednostek okazało się województwo Mazowieckie. Najbardziej odległe od niego są województwa: Lubelskie, Podkarpackie, Podlaskie, Świętokrzyskie i Warmińsko-mazurskie. Najbliższe województwu Mazowieckiemu okazało się województwo Wielkopolskie i Śląskie. Zauważmy, że w tej analizie nie uwzględnia się wartości składników głównych, a jedynie względne odległości między położeniami na płaszczyźnie utworzonej przez dwa najważniejsze składniki główne. Należy dodatkowo zaznaczyć, że powyższy rozkład został uzyskany przy uwzględnieniu jedynie wybranych 13 parametrów, spośród wielu dostępnych w publikacjach GUS i dotyczy danych jednego roku.