Podręcznik: Struktura rekurencyjna sieci separującej

3. Ślepa separacja sygnałów

3.3. Struktura rekurencyjna sieci separującej

W rozwiązaniu problemu separacji sygnałów statystycznie niezależnych J. Herault i C. Jutten zaproponowali sieć neuronową liniową ze sprzężeniem zwrotnym, przedstawioną na rys. 9.2.

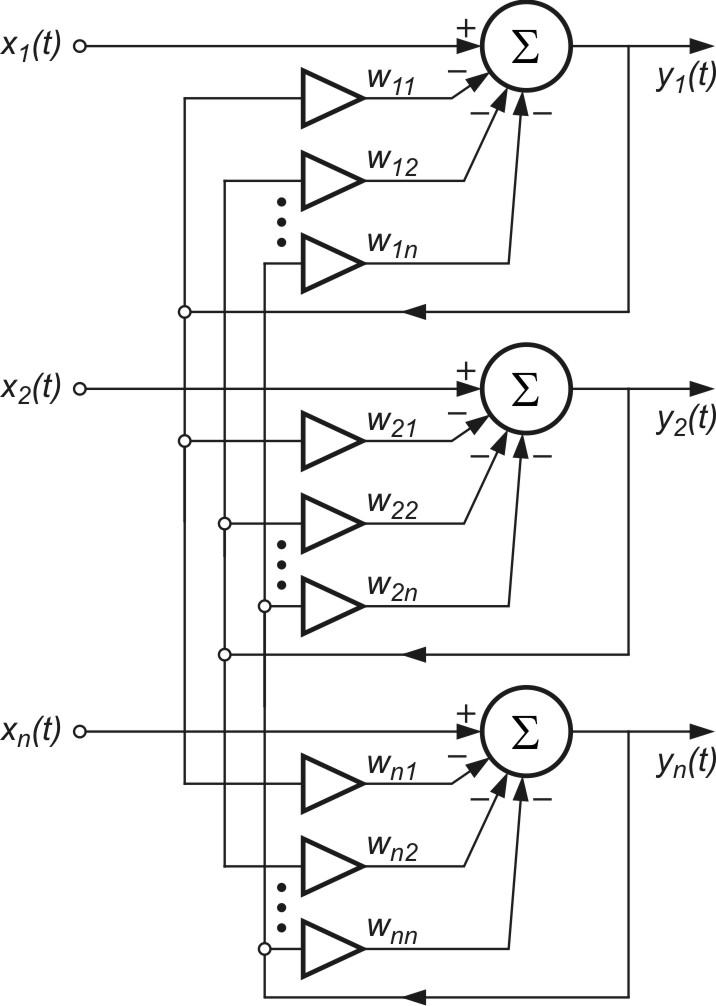
Rys. 9.2 Struktura sieci rekurencyjnej do ślepej separacji sygnałów

Sieć zawiera $n$ liniowych neuronów, powiązanych ze sobą przez wzajemne sprzężenia zwrotne. Wagi synaptyczne $w_{ij}$ w rozwiązaniu oryginalnym Heraulta i Juttena są różne od zera tylko przy sprzężeniach wzajemnych (zasada ta została odrzucona przez prof. Cichockiego pozwalając na lepsze działanie systemu). Każdy neuron w sieci generuje sygnał wyjściowy

$y_i(t)=x_i(t)-\sum_{j=1}^n w_{i j} y_j(t)$

(9.4)

Przy oznaczeniu przez $\mathbf{A}$ macierzy mieszającej, przez $\mathbf{W}$ macierzy wagowej (obie kwadratowe o tych samych wymiarach)

$\mathbf{W}=\left[\begin{array}{llll}w_{11} & w_{12} & \cdots & w_{1 n} \\ w_{21} & w_{22} & \cdots & w_{2 n} \\ \cdots & \cdots & \cdots & \cdots \\ w_{n 1} & w_{n 2} & \cdots & w_{n n}\end{array}\right]$

(9.5)

a przez $\mathbf{x}(t)$ , $\mathbf{s}(t)$ oraz $\mathbf{y}(t)$ wektorów odpowiednio obserwowanych sygnałów $x_i(t)$ przetworzonych według zależności (9.1), wektora sygnałów źródłowych $s_i(t)$ oraz wektora sygnałów wyjściowych $y_i(t)$ sieci, gdzie

$\mathbf{x}(t)=\left[\begin{array}{c}x_1(t) \\ x_2(t) \\ \cdots \\ x_n(t)\end{array}\right]$ ,

$\mathbf{s}(t)=\left[\begin{array}{c}s_1(t) \\ s_2(t) \\ \cdots \\ s_n(t)\end{array}\right]$ ,

$\mathbf{y}(t)=\left[\begin{array}{c}y_1(t) \\ y_2(t) \\ \ldots \\ y_n(t)\end{array}\right]$

(9.6)

działanie sieci z rys. 9.2 można opisać równaniem macierzowym

$\mathbf{y}(t)=\mathbf{x}(t)-\mathbf{W y}(t)$

(9.7)

Przy nieznanej macierzy mieszającej $\mathbf{A}$ i wektorze $\mathbf{s}(t)$ oraz założeniu statystycznej niezależności składników wektora $\mathbf{s}(t)$ , zadanie sieci sprowadza się do takiego określenia wektora rozwiązania $\mathbf{y}(t)$ , które umożliwi odtworzenie sygnałów pierwotnych $s_i(t)$ tworzących wektor $\mathbf{s}(t)$ . Z równania (9.7) wynika, że rozwiązanie takie musi spełniać warunek

$\mathbf{y}(t)=(\mathbf{1}+\mathbf{W})^{-1} \mathbf{x}(t)$

(9.8)

Wektor $\mathbf{y}(t)$ będzie odtwarzał wektor poszukiwanych sygnałów źródłowych $\mathbf{s}(t)$ . Odtworzenie to jest możliwe z dokładnością do pewnej, bliżej nieokreślonej skali $d_i$ , czyli $\mathbf{y}(t) = \mathbf{Ds}(t)$ gdzie $\mathbf{D}$ jest macierzą diagonalną, $\mathbf{D}=\operatorname{diag}\left\{d_1, d_2, \ldots, d_n\right\}$ , przy praktycznie dowolnej kolejności występowania poszczególnych składników $\mathbf{y}(t)$ w wektorze $\mathbf{y}(t)$ (przy nieznanej postaci składników wektora sygnałów źródłowych nie ma to praktycznie żadnego znaczenia). Stąd podstawowym celem jest rekonstrukcja „kształtu” sygnałów źródłowych. Innymi słowy, poszukiwanym systemem separującym jest taka macierz $\mathbf{W}$ , że zachodzi relacja

$\mathbf{y}(t)=\mathbf{W A s}(t)=\mathbf{P D s}(t)$

(9.9)

Można przyjąć, że macierz estymowana $\hat{\mathbf{A}}=\mathbf{W}^{+}$ jest w rzeczywistości określona jako $\hat{\mathbf{A}}=\mathbf{A P D}$ oraz $\mathbf{W A} \hat{\mathbf{A}}=\mathbf{W} \mathbf{W}^{+}=\mathbf{1}_n$ , gdzie $\mathbf{P}$ jest macierzą permutacji odpowiedzialnej za przestawienie kolejności składników wynikowych $y_i$ , $\mathbf{D}$ – macierz diagonalna skalująca wartości sygnałów wynikowych, $\mathbf{W}^{+}$ jest macierzą pseudo-odwrotną do macierzy $\mathbf{W}$ .

Rozwiązanie określające wektor $\mathbf{y}(t)$ spełniający warunek (9.8) jest możliwe do osiągnięcia przy dowolnej liczbie $n$ sygnałów. Przy większej niż dwa liczbie źródeł i nieznanych z góry wartościach współczynników $a_{ij}$ macierzy mieszającej można osiągnąć separację sygnałów, stosując jedynie metody algorytmiczne adaptacyjnego doboru wag sieci neuronowej.