Podręcznik
3. Ślepa separacja sygnałów
3.4. Algorytmy uczące sieci rekurencyjnej
Rozwiązanie problemu separacji sygnałów przy zastosowaniu sieci rekurencyjnej zostało zaproponowane przez J. Heraulta i C. Juttena i ulepszone przez Cichockiego [8] sprowadza się do rozwiązania układu równań różniczkowych, opisujących zmiany wag sieci neuronowej dla każdej chwili czasowej \(t\).
Zgodnie z modyfikacja Cichockiego wprowadza się sprzężenie zwrotne własne neuronu z wagą \(w_{i i} \neq 0\). Sprzężenie to powoduje samo-normalizację sygnałów wyjściowych, sprowadzając je wszystkie do takiego samego poziomu liczbowego (wartości znormalizowanej) i ułatwiając w ten sposób proces separacji. Wówczas zależności adaptacyjne wag opisane są wzorami (przy założeniu, że \(y_i(t)\) nie zawierają składowej stałej)
| \( \frac{d w_{i j}}{d t}=\eta(t) f\left(y_i(t)\right)g\left(y_j(t)\right) \) | (9.10) |
dla wag łączących różne neurony \( i \neq j\), oraz
| \( \frac{d w_{i i}}{d t}=\eta(t)\left[f\left(y_i(t)\right)g\left(y_i(t)\right)-1\right] \) | (9.11) |
dla kolejnych wag sprzężenia własnego (wagi diagonalne macierzy \(\mathbf{W}\)). Obie zależności można zapisać w postaci macierzowej wspólnej dla obu rodzajów wag
| \(\frac{d \mathbf{W}}{d t}=\eta(t)\left[\mathbf{f}(\mathbf{y}(t)) \mathbf{g}^T(\mathbf{y}(t))-\mathbf{1}\right]\) | (9.12) |
w której \(\mathbf{W}\) oznacza macierz wag sieci o wymiarze \( n \times n \), a \( \mathbf{f}(\mathbf{y}) \) i \( \mathbf{g}(\mathbf{y}) \) oznaczają wektory sygnałowe, \(\mathbf{f}(\mathbf{y})=\left[f\left(y_1(t)\right), f\left(y_2(t)\right), \ldots, f\left(y_n(t)\right)\right]^T\), \(\mathbf{g}(\mathbf{y})=\left[g\left(y_1(t)\right), g\left(y_2(t)\right), \ldots, g\left(y_n(t)\right)\right]^T\).
W praktyce stosuje się różne rodzaje funkcji \(f(x)\) i \(g(x)\), najczęściej przyjmując jedną z nich typu wypukłego, a drugą typu wklęsłego. Przykładowy wybór funkcji to \(f(x)=x^3\), \(f(x)=x^5\). W przypadku funkcji \(g(x)\) dobre rezultaty uzyskuje się przy \(g(x)=tanh(x)\), \(g(x)=arctg(x)\), \(g(x)=x\), \(g(x)=sgn(x)\), itp. Jak zostało udowodnione w pracy [8] obie funkcje \(f(x)\) oraz \(g(x)\) odpowiadają momentom statystycznym wyższych rzędów, które przy założeniu statystycznej niezależności sygnałów automatycznie zapewniają wartość średnią \( \overline{f\left(y_i(t)\right) g\left(y_i(t)\right)} \) równą zeru, co jest warunkiem zbieżności algorytmu uczącego. Wybór współczynnika uczenia \( \eta(t) \) odgrywa istotną rolę w procesie adaptacji. W przypadku sygnałów stacjonarnych na początku uczenia jest to wartość stała, a następnie maleje do wartości minimalnej w miarę upływu czasu.
Z rozwiązania układu równań różniczkowych opisanych zależnością (9.12) otrzymuje się aktualne wartości wag, służące do określenia sygnałów wyjściowych opisanych wektorem \(\mathbf{y}(t)\), przy czym przy \(\mathbf{y}(t)=(\mathbf{1}+\mathbf{W})^{-1} \mathbf{x}(t)\).
Głównym źródłem zwiększonej efektywności algorytmu jest samo-normalizacja (do wartości jednostkowej) sygnałów wyjściowych \(y_i(t)\). Mianowicie w stanie ustalonym \(\frac{d \mathbf{W}}{d t}=\mathbf{0}\), skąd wynika, że \( \overline{f\left(y_i(t)\right) g\left(y_i(t)\right)} = 1 \), co oznacza, że niezależnie od aktualnego poziomu sygnałów \(s_i(t)\) następuje automatyczne skalowanie wszystkich sygnałów w sieci do poziomu jednostkowego. Badania symulacyjne sieci o zmodyfikowanym algorytmie uczenia wykazały, że możliwa jest separacja sygnałów o amplitudach różniących się nawet w stosunku \( 1 : 10^9 \).
Program został przetestowany przy separacji wielu różnorodnych sygnałów, wykazując się bardzo dobrą skutecznością.
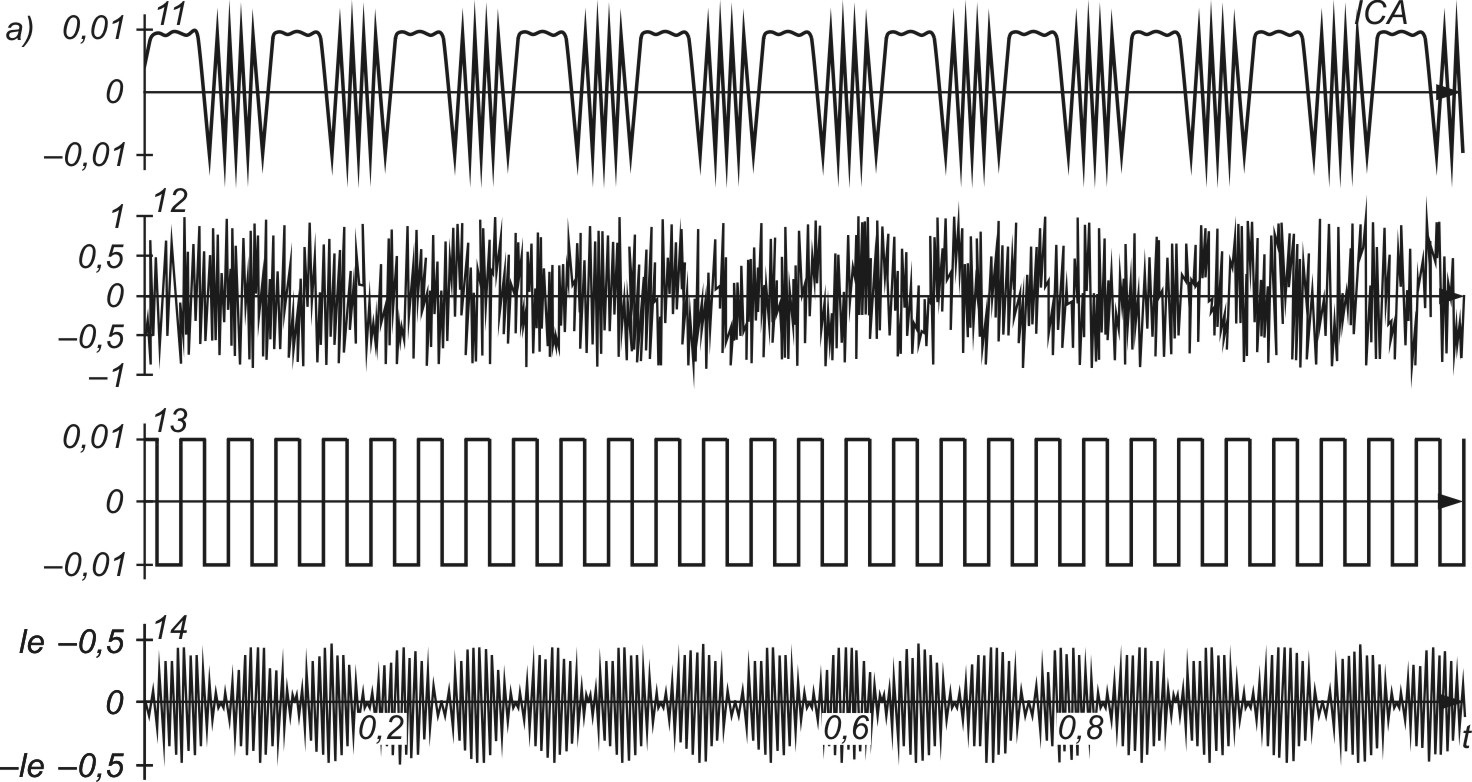
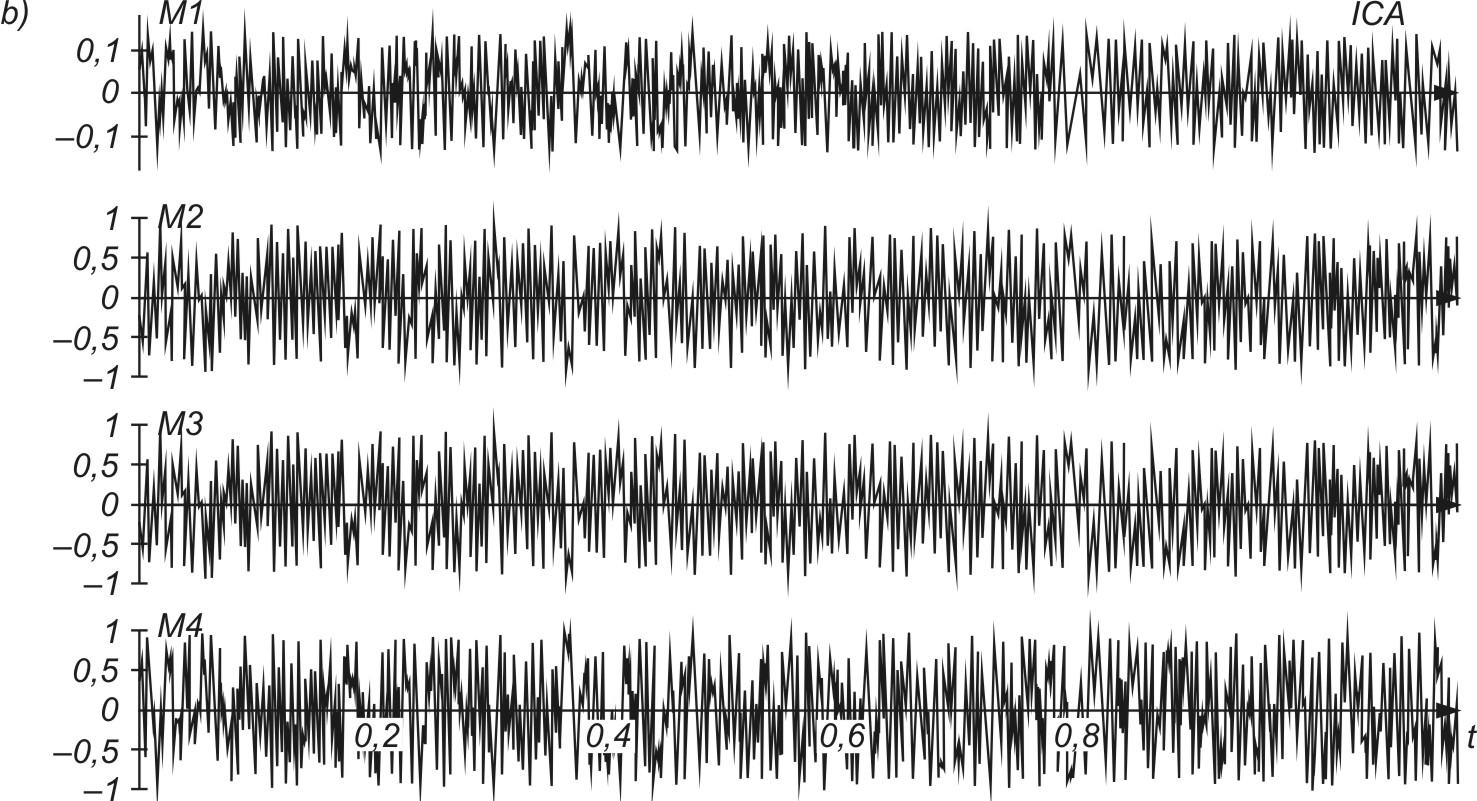
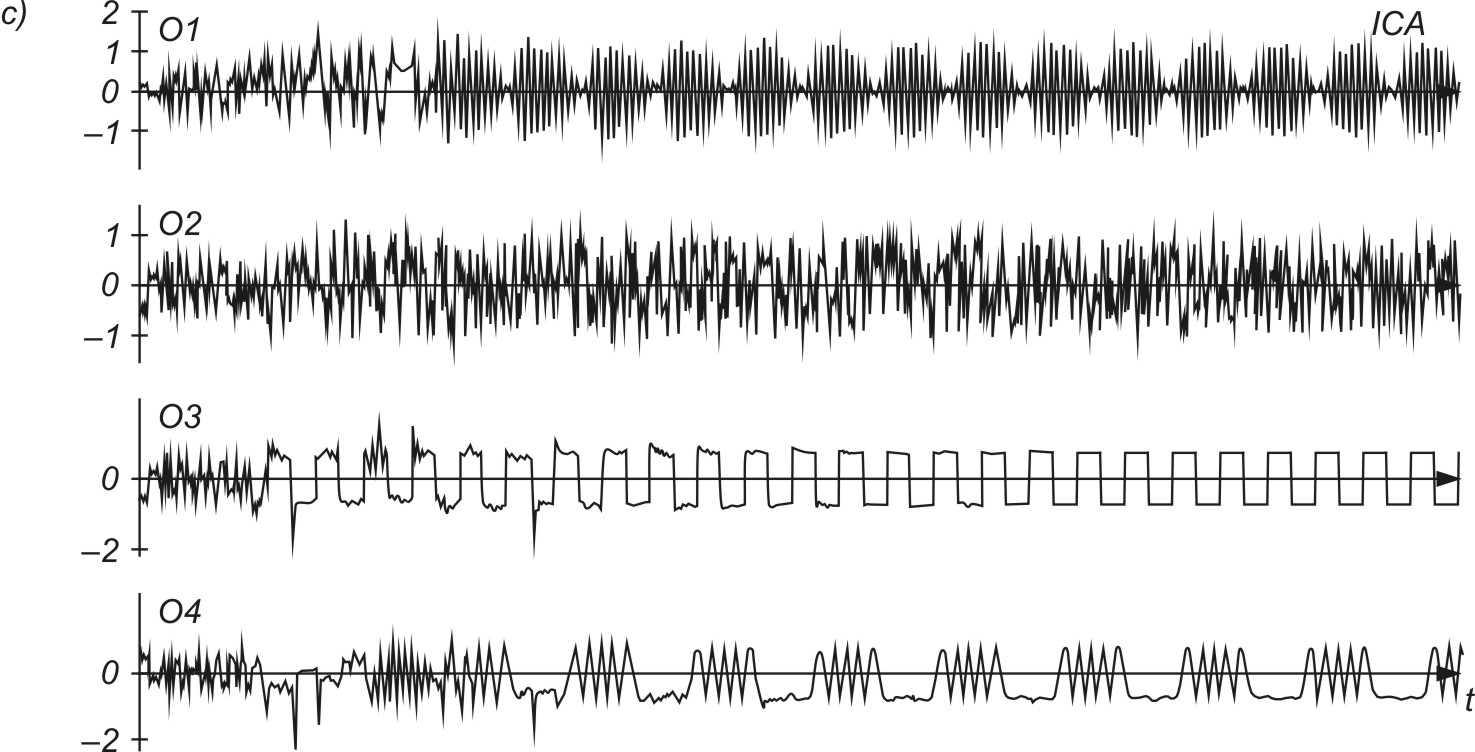
Na rys. 9.3 przedstawiono ilustracje procesu separacji czterech sygnałów si(t) o znacznie różniących się amplitudach
\(\begin{aligned} & s_1(t)=0,001 \sin (300 t+6 \cos (60 t)) \\ & s_2(t)=\operatorname{rand}(0,00001, t) \\ & s_3(t)=0,001 \operatorname{sgn}(\cos (155 t)) \\ & s_4(t)=0,00001 \sin (1200 t) \sin (50 t)\end{aligned}\)
Rys. 9.3a przedstawia (u góry) sygnały oryginalne \(s_i(t)\), rys. 9.3b - sygnały zmieszane \(x_i(t)\), a rys. 9.3c (na dole) - sygnały estymowane przez sieć neuronową w procesie separacji (sygnały niezależne będące repliką sygnałów oryginalnych). Sygnałami wejściowymi sieci neuronowej są sygnały zmieszane (trzy środkowe wykresy czasowe na rys. 9.3b). Ze względu na ogromną różnicę amplitud sygnałów oryginalnych w sygnałach zmieszanych podawanych na sieć widoczne są jedynie największe sygnały szumu, natomiast sygnały o małej amplitudzie są niezauważalne.
Proces separacji przeprowadzony został przy zastosowaniu funkcji nieliniowych \(f(x) = x^3\) i \(f(x) = tgh(10x)\) oraz współczynniku uczenia \( \eta(t) \) zmienianym adaptacyjnie przy wartości startowej równej 2000. Taki dobór parametrów pozwolił na separację wszystkich sygnałów, niezależnie od poziomu amplitud (trzy dolne wykresy czasowe na rys. 9.3c). Odseparowane przez sieć sygnały charakteryzowały się jednakowym poziomem amplitud, uzyskanym dzięki wprowadzeniu sprzężenia własnego neuronów. Ich kolejność występowania jest inna niż kolejność sygnałów oryginalnych.
