Podręcznik: Prognozowanie wskaźnika inflacji

3. Przykłady zastosowań sieci neuronowych w zadaniach biznesowych

3.2. Prognozowanie wskaźnika inflacji

Inflacja jest zjawiskiem monetarnym wywołanym szybszym przyrostem ilości pieniądza niż produkcji. W efekcie obserwuje się na rynku długotrwały wzrost średniego poziomu cen dóbr i usług konsumpcyjnych i nie konsumpcyjnych wchodzących do tak zwanego koszyka dóbr. Lista tych dóbr i usług jest każdorazowo określona przez Główny Urząd Statystyczny i ewentualnie nowelizowana odpowiednio do preferencji konsumentów.

13.2.1 Wprowadzenie

Miernikiem inflacji stosowanym praktyce jest indeks cen towarów i usług konsumpcyjnych, definiowany jako stosunek kosztów określonych dóbr konsumpcyjnych wchodzących w skład koszyka do kosztów tych samych dóbr w okresie przyjętym za bazowy.

Inflacja jest faktem obiektywnym i poprzez swój związek z wartością pieniądza i stopami procentowymi musi być brana pod uwagę przy podejmowaniu decyzji związanych z inwestowaniem i zarządzaniem finansami. Istnieje więc potrzeba prognozowania indeksu cen, ponieważ oczekiwania inflacyjne wpływają na wiele decyzji biznesowych podejmowanych w skali zarówno mikro- jak i makroekonomicznej.

Na inflację wpływa aktualny popyt na określone towary na rynku jak również sfera produkcji oraz organizacja współczesnego społeczeństwa. Jednym z najistotniejszych elementów który musi być określony w modelu prognozy jest zdefiniowanie cech diagnostycznych, które będą wpływały w sposób bezpośredni na wynik prognozy. W niniejszych badaniach uwzględnione będą następujące wielkości odniesione do kolejnych miesięcy:

wskaźnik cen i usług konsumpcyjnych ( ${wcu}$ )
średnia płaca miesięczna ( ${spm}$ )
stopa bezrobocia ( ${sb}$ )
wartość produkcji sprzedanej w przemyśle ( ${wps}$ )

W prognozie na dany miesiąc brać będziemy pod uwagę powyższe wielkości odniesione do określonej liczby miesięcy z przeszłości.

13.2.2 Model neuronowy predykcji

Podstawowym elementem, który musi być rozwiązany w pierwszej kolejności jest wybór i ewentualna selekcja cech diagnostycznych, które będą uwzględniane w modelu. Cztery wymienione wyżej czynniki brane pod uwagę w modelu mogą dotyczyć wiele miesięcy wstecz, pozwalając w ten sposób na uwzględnienie dynamiki ich zmian na wartość prognozowanego wskaźnika cen i usług. Ponadto jako cechy diagnostyczne mogą być traktowane same wielkości bądź ich miesięczne przyrosty. W naszym modelu neuronowym prognozy wzięto pod uwagę każdy z 4 wymienionych wyżej czynników biorąc pod uwagę ich wielkości rzeczywiste. Dla zapewnienia porównywalności wpływu każdej wielkości wszystkie zmienne związane z prognozą podlegały normalizacji według wzoru

$x_n=\frac{x_{rz}-x_{\min }}{x_{\max }-x_{\min }}$

(13.1)

We wzorze tym $x_{rz}$ oznacza wielkość rzeczywistą, $x_{n}$ – wartość znormalizowaną, $x_{min}$ – wartość minimalną a $x_{max}$ – wartość maksymalną zmiennej $x$ .

Przy wyborze ilości miesięcy branych wstecz dla uwzględnienia trendu zmian dla każdej z 4 cech prognostycznych zdecydowano się uwzględniać ich wartości z trzech poprzedzających miesięcy. Stąd przy prognozowaniu współczynnika cen i usług na miesiąc $m$ -ty wektor wejściowy $\mathbf{x}$ w prognozie miał postać:

$\mathbf{x}=[{wcu}(m-1), \ldots, {wcu}(m-3), {spm}(m-1), \ldots, {spm}(m-3), {sb}(m-1), \ldots, {sb}(m-3), {wps}(m-1), \ldots, {wps}(m-3)]$

Jest to wektor 12-elementowy. Prognoza dotyczyć będzie wskaźnika cen towarów i usług konsumpcyjnych w odniesieniu do tego samego miesiąca sprzed roku. W eksperymentach numerycznych wykorzystano dostępną aktualnie bazę danych GUS z lat od stycznia 1999 do czerwca 2006. Zawiera ona dane dotyczące 126 miesięcy. Na rys. 13.1 przedstawiono graficznie wartości wskaźników dotyczące tych miesięcy.

Rys. 13.1 Wykres zmian wskaźnika

${wcu}$ dla 126 miesięcy w bazie danych GUS z lat 1999-2009

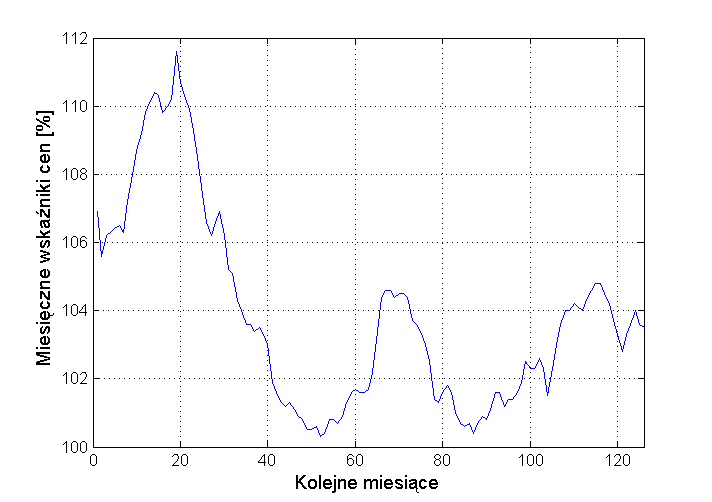
Połowa z tych danych (63) została użyta w uczeniu a druga połowa pozostawiona do testowania wytrenowanej sieci. Dane użyte w uczeniu i testowaniu podlegały wyborowi losowemu (funkcja randperm Matlab) a wszystkie obliczenia powtarzane 10-krotnie z obliczeniem wartości średnich błędów.

13.2.3 Wyniki badań eksperymentalnych prognozy

Badania zdolności prognostycznych sieci neuronowych w problemie predykcji wskaźnika cen towarów i usług przeprowadzono dla dwu rodzajów sieci neuronowych: sieć perceptronowa (MLP) oraz SVM. W przypadku sieci MLP zastosowana struktura miała postać: 12-5-1 (liczba neuronów ukrytych została dobrana w wyniku eksperymentów wstępnych). Sieć SVM do regresji posiadała identyczną liczbę wejść (12) i jedno wyjście. Liczba funkcji jądra jest natomiast dobierana automatycznie przez program uczący na podstawie danych uczących i wartości hiperparametrów. W uczeniu zastosowano stałą regularyzacji $C=1000$ , współczynnik tolerancji $\varepsilon=0,02$ i jądro gaussowskie o stałej $\gamma=0,008$

Prognozowane wartości wskaźnika ${wcu}$ zostały porównane z odpowiednimi wartościami rzeczywistymi wziętymi z bazy danych GUS. Jako miary jakości zastosowano trzy podstawowe rodzaje błędów ( $n$ oznacza liczbę miesięcy uczestniczących w teście, ${wcu}(m)$ – rzeczywistą wartość wskaźnika ${wcu}$ w miesiącu $m$ , $\widehat{wcu}$ - wartość przewidywaną przez program):

Średni względny błąd procentowy (MAPE)

$\text { MAPE }=\frac{1}{n} \sum_{m=1}^n \frac{|wcu(m)-\widehat{wcu}(m)|}{\left|wcu(m)\right|} \cdot 100 \%$

(13.2)

Maksymalny błąd względny procentowy (MAXPE)

$MAXPE=\max \frac{|w c u(m)-\widehat{wcu}(m)|}{\left|wcu(m)\right|} \cdot 100 \%$

(13.3)

Średniokwadratowy błąd procentowy (RMSE)

$RMSE=\sqrt{\frac{1}{n} \sum_{m=1}^n\left(\frac{wcu(m)-\widehat{wcu}(m)}{ (wcu(m)} \right)^2} \cdot 100 \%$

(13.4)

W tabeli 13.1 zestawiono uzyskane wartości błędów prognozy dla danych testujących (63 miesiące) nie uczestniczących w uczeniu.

Tabela 13.1 Zestawienie błędów prognozy dla danych testujących nie uczestniczących w uczeniu sieci neuronowych

	MAPE	RMSE	MAXPE
SVM	0.31%	1.47	2.45%
MLP	0.58%	1.97	3.85%

Uzyskane wartości błędów świadczą o bardzo dobrym działaniu predykcyjnym sieci neuronowych. Zarówno błędy średnie jak i maksymalne pozostają na małym (akceptowalnym w praktyce) poziomie. Na rys. 13.2 przedstawiono na wspólnym wykresie wartości wskaźnika inflacji wcu prognozowane przez sieć SVM oraz wielkości rzeczywiste (wykres górny). Na wykresie dolnym zobrazowano zmiany miesięczne błędów predykcji wyrażone w procentach.

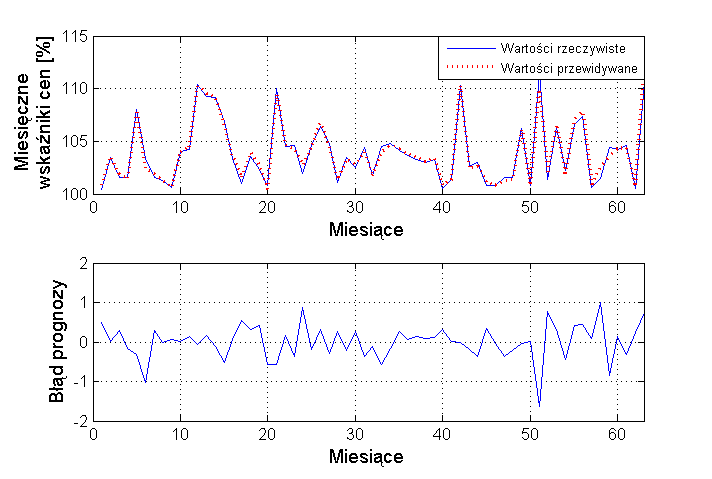
Rys. 13.2 Zestawienie prognozowanych wartości miesięcznych wskaźników

$wcu$ na tle wartości rzeczywistych (wykres górny) oraz błędów predykcji (wykres dolny)

Widoczna jest bardzo dobra zgodność wielkości prognozowanych i rzeczywistych. Błąd prognozy pozostaje na bardzo małym (zbliżonym do zera) poziomie.