Podręcznik

Jako przykład zastosowania zespołu klasyfikatorów pokażemy jego działanie przy rozpoznaniu obrazów twarzy. Jako narzędzie klasyfikacyjne zastosowane zostaną sieci głębokie CNN powiązane w zespole. Istnieje aktualnie kilkanaście dostępnych w Matlabie sieci pre-trenowanych, miedzy innymi alexnet, shufflenet, darknet53, efficientnetb0, squeezenet, googlenet; inceptionv3, mobilenetv2, resnet50, xception, inceptionresnetv2, nasnetmobile, densenet201. Zespół sieci można tworzyć na wiele sposobów. Jednym z nich jest przyjęcie jednego rodzaju sieci i wielokrotne powtórzenie procesu z losowymi wartościami startowymi i zmieniona strukturą końcową. Inny sposób to zastosowanie wielu różnych rozwiązań na raz w zespole. Badanie obu rozwiązań zostanie zaimplementowane w rozpoznaniu obrazów twarzy tworzących 68 klas. Każda klasa była reprezentowana przez 20 przykładowych próbek. Różnice między członkami tych samych klas są duże, co pokazano dla 3 klas na rys. 11.2.

Przykładowa implementacja programu w Matlabie:

% Program w Matlabie do rozpoznania obrazów twarzy przy użyciu zespołu pre-trenowanych sieci CNN
addpath 'pliki'
addpath 'pliki2'
addpath 'pliki3'
wyn=[]; wynVal=[];
Pred_y=[]; Pred_yVal=[]; time=[];
%% %Load Data
imds = imageDatastore( 'c:\chmura\ALEX_obrazy_all',...
'IncludeSubfolders',true,...
'ReadFcn', @customreader, ...
'LabelSource','foldernames');
[imdsTrain,imdsValidation] = splitEachLabel(imds,0.7,'randomized');
kk=10;
for i=1:kk
i
tic
% if i==1
net = alexnet;
% elseif i==2
% net = shufflenet;
% elseif i==3
% net = darknet53;
% elseif i==4
% net=efficientnetb0;
% elseif i==5
% net = squeezenet;
% elseif i==6
% net = googlenet;
% elseif i==7
% net = inceptionv3;
% elseif i==8
% net = mobilenetv2;
% elseif i==9
% net = resnet50;
% elseif i==10
% net = xception;
% elseif i==11
% net = inceptionresnetv2;
% elseif i==12
% net = nasnetmobile;
% elseif i==13
% net = densenet201;
% else
% end
analyzeNetwork(net)
net.Layers(1)
inputSize = net.Layers(1).InputSize;
lgraph = layerGraph(net);
[learnableLayer,classLayer] = findLayersToReplace(lgraph);
[learnableLayer,classLayer]
numClasses = numel(categories(imdsTrain.Labels));
if isa(learnableLayer,'nnet.cnn.layer.FullyConnectedLayer')
newLearnableLayer = fullyConnectedLayer(numClasses, ...
'Name','new_fc', ...
'WeightLearnRateFactor',10, ...
'BiasLearnRateFactor',10);
elseif isa(learnableLayer,'nnet.cnn.layer.Convolution2DLayer')
newLearnableLayer = convolution2dLayer(1,numClasses, ...
'Name','new_conv', ...
'WeightLearnRateFactor',10, ...
'BiasLearnRateFactor',10);
end
lgraph = replaceLayer(lgraph,learnableLayer.Name,newLearnableLayer);
newClassLayer = classificationLayer('Name','new_classoutput');
lgraph = replaceLayer(lgraph,classLayer.Name,newClassLayer);
figure('Units','normalized','Position',[0.3 0.3 0.4 0.4]);
plot(lgraph)
ylim([0,10])
layers = lgraph.Layers;
connections = lgraph.Connections;
layers(1:10) = freezeWeights(layers(1:10));
lgraph = createLgraphUsingConnections(layers,connections);
%TRAIN
pixelRange = [-30 30];
scaleRange = [0.9 1.1];
imageAugmenter = imageDataAugmenter( ...
'RandXReflection',true, ...
'RandXTranslation',pixelRange, ...
'RandYTranslation',pixelRange, ...
'RandXScale',scaleRange, ...
'RandYScale',scaleRange);
augimdsTrain = augmentedImageDatastore(inputSize(1:2),imdsTrain, ...
'DataAugmentation',imageAugmenter);
augimdsValidation = augmentedImageDatastore(inputSize(1:2),imdsValidation);
miniBatchSize = 10;
valFrequency = floor(numel(augimdsTrain.Files)/miniBatchSize);
options = trainingOptions('sgdm', ...
'MiniBatchSize',miniBatchSize, ...
'MaxEpochs',5, ...
'ExecutionEnvironment','gpu',...
'InitialLearnRate',3e-4, ...
'Shuffle','every-epoch', ...
'ValidationData',augimdsValidation, ...
'ValidationFrequency',valFrequency, ...
'Verbose',false, ...
'Plots','training-progress');
net = trainNetwork(augimdsTrain,lgraph,options);
[YPred,probs] = classify(net,augimdsValidation);
accuracy = mean(YPred == imdsValidation.Labels)
%i=i+1
toc
%STATYSTYKA
Pred_y=[double(YPred) double(imdsValidation.Labels)];
dtest=double(imdsValidation.Labels);
wyn=[wyn accuracy]
time=[time toc]
end
nclass=numClasses
%ZESPÓŁ
dy=[dtest Pred_y]
nclass=numClasses
clear dz
[lw,lk]=size(dy);
for i=1:lw
for j=1:nclass
d=0;
for k=2:lk
if (j==double(dy(i,k)))
d=d+1;
else
end
end
dz(i,j)=d;
% klasa=dy(:,1)
end
end
dz;
[q,cl_max]=max(dz');
zgod_class=length(find(double(dy(:,1))==cl_max'));
dokl_zesp=zgod_class/lw*100
median_zesp=median(wyn)
max_zesp=max(wyn)
mean_zesp=mean(wyn)
odch_zesp=std(wyn)
[C,order] = confusionmat(double(dtest),double(cl_max));
Confusion=C
for i=1:nclass,
sen(i)=C(i,i)/sum(C(i,:));
end
for i=1:nclass,
prec(i)=C(i,i)/sum(C(:,i));
end
lc1t=sum(dtest==1);
lc2t=sum(dtest==2);
%ROC
for i=1:length(dtest)
ydz(i)=dz(i,1)/(dz(i,1)+dz(i,2));
end
for i=1:lc1t
dtestroc(i)=1;
end
for i=lc1t+1:length(dtest)
dtestroc(i)=0;
end
wyn
sen
prec
F1_zesp=2*prec.*sen./(prec+sen)
time

Program stosuje aktualnie 10 członków zespołu (kk=10), generując wyniki poszczególnych członków oraz wyniki zespołu zintegrowanego poprzez głosowanie większościowe. W efekcie obliczone są takie miary jakości, jak dokładność, precyzja, czułość i miara F1 rozpoznania poszczególnych klas. Wyniki rozpoznania klas przedstawione zostaną dla 2 rozwiązań. Pierwszy zespół został zbudowany na bazie ALEXNET, wywołanym 10 razy z losowymi wartościami parametrów startowych. W drugim przypadku zespół złożony by z 10 różnych struktur sieci (w kolejności zadeklarowanej w liniach programu w Matlabie).

Tabela 11.2 przedstawia wartości średnie dokładności rozpoznania wszystkich klas przez klasyfikator ALEXNET w kolejnych próbach działania na tych samych danych testujących oraz przy zastosowaniu 10 różnych struktur sieciowych (kolejność jak w programie)

Tabela 11.2 Średnia dokładność rozpoznania 68 klas przez 2 zespoły: zespół zbudowany na bazie ALEXNET
i zespół złożony z 10 różnych struktur sieciowych CNN

Zastosowanie integracji wyników poszczególnych klasyfikatorów metodą głosowania większościowego zdecydowanie poprawiło końcową dokładność rozpoznania, która dla zespołu zbudowanego na bazie ALEXNET jest równa 94.12% (wzrost dokładności względem wartości średniej klasyfikatorów o 12.8%). W drugim przypadku ten przyrost był znacznie mniejszy ( z wartości 77.87 do 81.37%). Tym razem znacznie lepsze wyniki uzyskano w zespole zbudowanym na bazie jednego rodzaju sieci. Gorszy wynik zespołu zbudowanego z różnych sieci był spowodowany niewydolnością aż 3 rodzajów rozwiązań (sieć 4, 5 i 10) dla których dokładność rozpoznania była bardzo niska i zdecydowanie odbiegała od średniej pozostałych rozwiązań. Eliminacja tych słabszych sieci z zespołu pozwala uzyskać znacznie lepsze wyniki, przewyższające wyniki zespołu zbudowanego na bazie jednej sieci.

Należy przy tym zauważyć, że głosowanie większościowe (jakkolwiek najprostsze) nie zapewnia w każdym przypadku lepszych wyników zespołu niż najlepszy klasyfikator indywidualny ze względu na duże różnice dokładności poszczególnych rozwiązań (jest to widoczne w drugim przypadku eksperymentów).

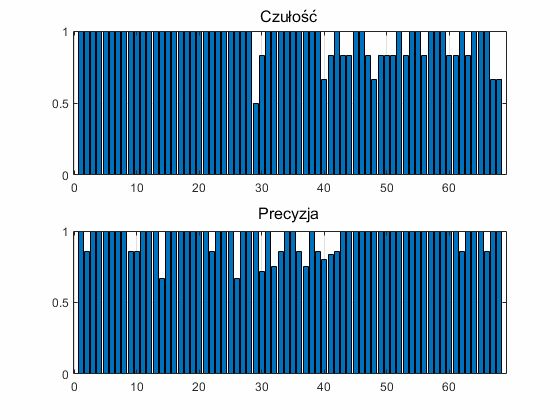
Na rys. 12.3 przedstawiono wartości czułości i precyzji klasowej uzyskanej dla poszczególnych klas przez zespół klasyfikatorów. Wartość średnia precyzji klasowej jest równa 95.22%, natomiast czułości rozpoznania klas przez zespół równa 94.12%. Oba wyniki można uznać za bardzo dobre biorąc pod uwagę liczbę rozpoznawanych klas (68) jak i duże różnice w reprezentacji próbek należących do tej samej klasy.

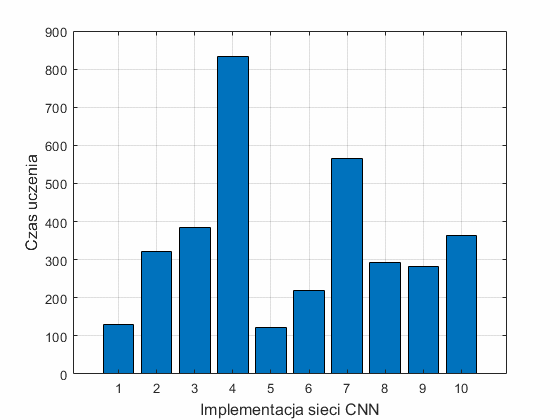
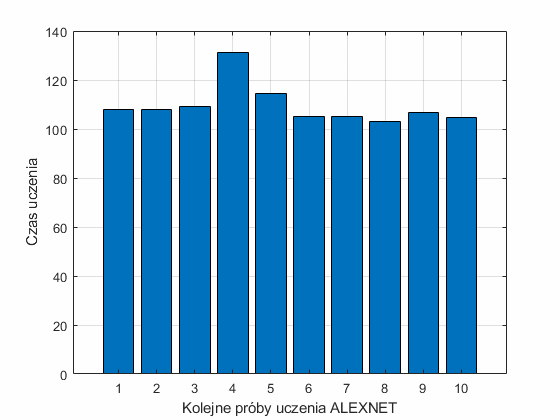
Interesujące są również czasy działania poszczególnych implementacji sieci CNN. Na rys. 12.4 przedstawiono 2 wykresy ilustrujące czasy potrzebne na treningi poszczególnych rozwiązań sieci. Rys. 12.4a przedstawia czasy uczenia różnych implementacji sieci CNN, natomiast rys. 12.4b czas uczenia tej samej sieci ALEXNET w 10 kolejnych próbach.

Najdłuższy czas uczenia odpowiadał sieci czwartej (efficientnetb0) oraz sieci siódmej (inceptionv3). Najmniej wymagająca pod względem czasowym okazała się sieć piąta (squeezenet) oraz pierwsza (ALEXNET). Niewielkie różnice w czasach uczenia zaobserwować można przy powtarzanych próbach uczenia sieci ALEXNET. Średni czas w tych próbach był równy 109.5 sekund, przy odchyleniu standardowym 8.2 sekund.