Poprzedni
Następny  

Rozdział 2. PODSTAWOWE OPERACJE RASTROWE

2.1. Rysowanie odcinka i łuku okręgu

Jednym z podstawowych problemów tego typu jest zadanie narysowania odcinka na mapie pikseli. Analizując rysunek odcinka na mapie pikseli (rys.2.1) można zaproponować prosty sposób postępowania: należy rysować od lewej do prawej zwiększając za każdym razem o 1 współrzędną x , czasem zwiększając y , kiedy wynika to z położenia punktu odcinka. Jednocześnie w tym problemie można wykorzystać symetrie osiowe w kartezjańskim układzie współrzędnych. Zmiana nachylenia odcinka – powyżej 45 wymagałaby zmiany postępowania (rysować od dołu do góry zwiększając y o 1 , przy czym w zależności od położenia punktu powiększając x o 1). Ale przecież jest to tylko zamiana współrzędnych. Algorytm postępowania pozostaje bez zmian. Analizując w ten sposób odcinki o dowolnych nachyleniach (dowolne współrzędne początku i końca odcinka) można zauważyć, że wystarczy zaproponować skuteczny algorytm rysowania dla odcinków, których nachylenie mieści się w przedziale od 0o do 45o. Pozostałe przypadki można uzyskać stosując ten sam algorytm dla zamienionych współrzędnych lub zmieniając znak przed odpowiednią współrzędną.

 Najprostszym rozwiązaniem zadania wydaje się poprowadzenie prostej przez końce odcinka i opisanie jej równaniem . Następnie wyznaczenie wartości  dla całkowitych wartości  odpowiadających kolejnym kolumnom pikseli. Jeśli teraz przybliżymy współrzędne  do wartości całkowitej, to otrzymamy współrzędne dla kolejnych pikseli tworzących odcinek tzn.  , gdzie  jest operacją zaokrąglania do najbliższej wartości całkowitej. Tak skonstruowany algorytm przyrostowy ma podstawową wadę. Wymaga operacji zmiennopozycyjnych (mnożenia, dodawania, zaokrąglania).



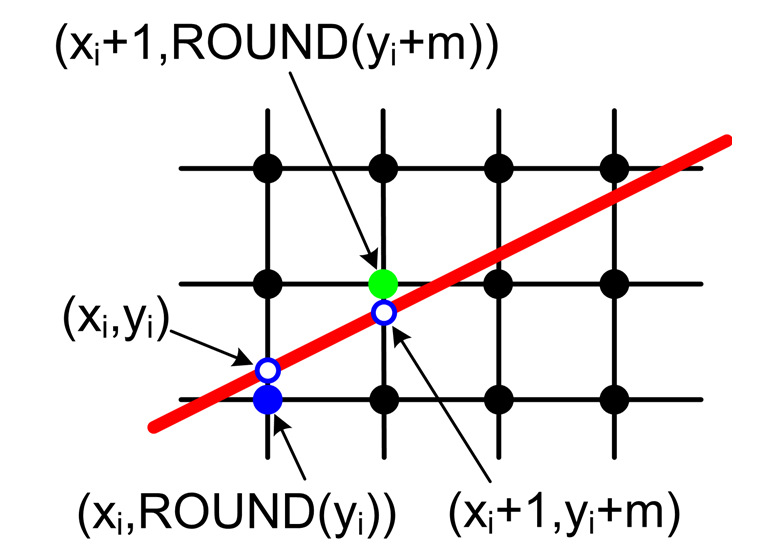
Rys.2.2. Rysowanie odcinka, algorytm wykorzystujący operacje zmiennopozycyjne.
Piksele na tym rysunku zostały zaznaczone jako węzły siatki kolejnych wartości współrzędnych.

Najprostsza procedura rysowania odcinka Line dla x2>x1, y2>y1, 0<m<1 .:

procedure Line (x1, x2, y2, y2,)
begin
    dx := x2-x1;   dy := y2-y1
    m := dy/dx;    y := y1;
    for xINTEGER:=x1 to x2 do
                begin
                      set_pixel(xINTEGER, ROUND( y ));
                      y=y+m;
                end;
end;

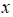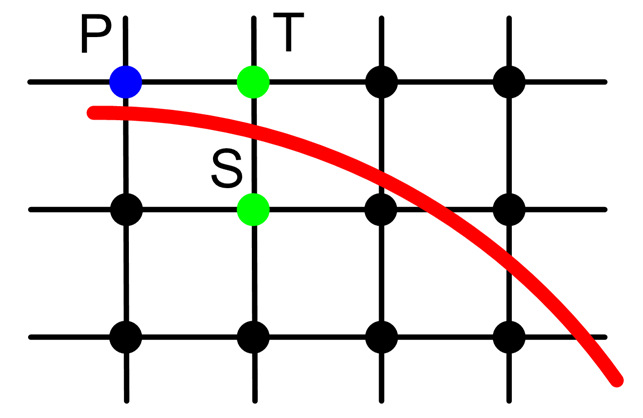
Rozwiązanie oparte w całości na arytmetyce stałopozycyjnej zaproponował Bresenham w 1965 roku. Jest to algorytm przyrostowy, w którym jedna współrzędna np.   wzrasta w każdym kroku o 1, tzn.   . Bez zmniejszania ogólności można przyjąć, że wystarczy opracować algorytm dla nachylenia odcinka od 0 do 1. Dla innych wartości można bowiem odpowiednio zamienić zmienne.  Wzrost   w takim przypadku zależy od wyboru piksela, który jest bliżej teoretycznej prostej (S lub T  na rysunku 2.3).  O wyborze decyduje zmienna kontrolna d , która jest uaktualniana w każdym kroku.

Jeśli di < 0  (piksel S ) to .

Jeśli di >= 0 (piksel T ) to   .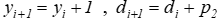

Przy czym wartość początkowa   oraz   , gdzie dx , dy są różnicami współrzędnych między końcem a początkiem odcinka.


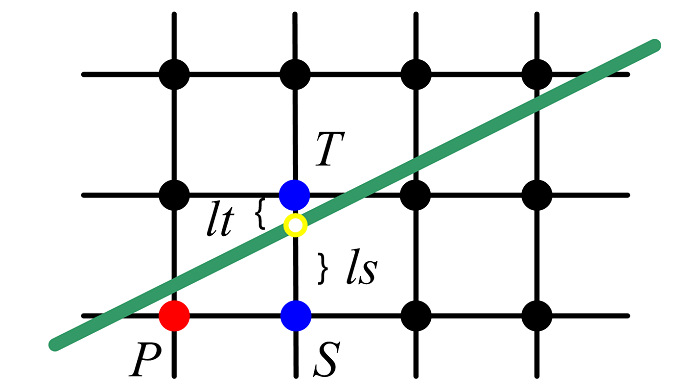
Rys.2.3. Wybór punktów w algorytmie Bresenhama rysowania odcinka.
Z bieżącego piksela P wybieramy piksel następny spośród pikseli T i S.
Przecięcia linii pionowych i poziomych czarnej kraty oznaczają środki pikseli.


Pełny algorytm Bresenhama dla x2>x1, y2>y1, 0<m<1 wyglądałby tak:

procedure Bresline (x1,x2, y2,y2,)
begin
            dx := x2-x1;  dy := y2-y1
            p1 := 2*dy-dx;  p2 := 2*(dy-dx);
            x := x1;  y := y1;
            xend := x2;
            set_pixel(x,y);
            while (x<xend) do begin
                        x := x+1;
                        if (d<0) d := d+p1;
                        else begin
                                    d := d+p2;
                                    y := y+1;
                        end;
                        set_pixel(x,y);
            end;
end;

Algorytm taki, wykorzystujący tylko operacje całkowite jest również użyteczny w rozwiązaniach sprzętowych. Takie, podobne i bardziej skomplikowane zadania we współczesnych kartach graficznych realizowane są sprzętowo.

 Omawiany w rozdziale 1. problem próbkowania jest już widoczny w przypadku najprostszego zadania. Korzystanie z rastra w przypadku rysowania odcinka może prowadzić do następujących problemów.:

Pierwszym jest problem „schodków” (rys.2.4). Poprawę wyświetlania można uzyskać przez odpowiednią modyfikację barw pikseli sąsiednich.

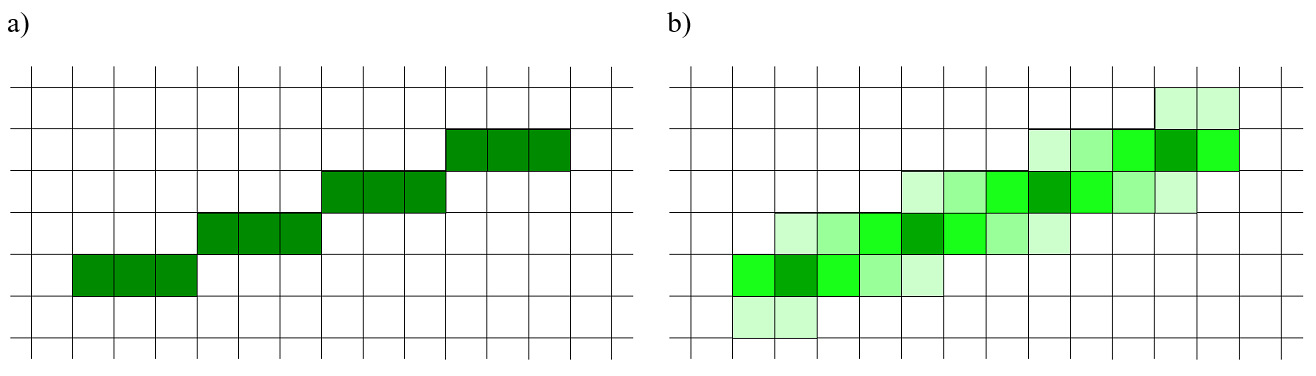
Rys.2.4. a) Proste rysowanie odcinka na rastrze (algorytm naiwny).
b) Rysowanie odcinka + algorytm antyaliasingu  (jasność/luminancja proporcjonalna
do powierzchni „zakrywanej” przez teoretyczny odcinek).

Drugim problemem jest fakt, że odcinek może nie być symetryczny gdy zamienimy końce startowe. Problem ten wymaga korekty podejmowania decyzji dla  d=0 w zależności od wzrostu lub spadku wartości współrzędnych.

Trzecim, chyba najmniej spodziewanym problemem jest postrzegana zmiana jasności (i/lub szerokości odcinka) związana z położeniem i nachyleniem odcinka. Oba odcinki na rysunku 2.5 składają się z 7 punktów. Tylko że odcinek po przekątnej rastra jest   razy dłuższy od odcinka poziomego. Jest to problem związany ze skończoną rozdzielczością rastra i powstaje podobnie do problemu „schodków” odcinka.

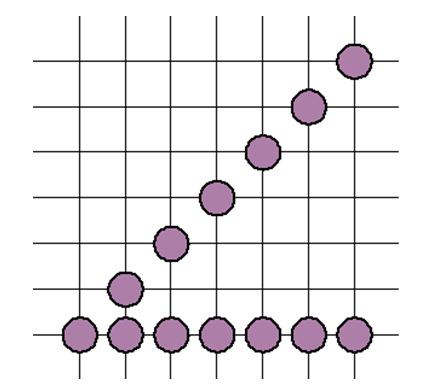
Rys.2.5. Odcinki o różnej długości zbudowane na mapie pikseli z 7 punktów.

Rozwiązanie tego problemu wymaga zmiany barwy sąsiednich pikseli – analogicznie do rozwiązania problemu „schodków”. Zakłada się, że odcinek ma określoną szerokość – odcinek jest prostokątem o szerokości jednego piksela i zadanej długości. Jeśli taki prostokąt umieścimy pod dowolnym katem na mapie pikseli to przykryje częściowo pewne piksele. Przyjmując zmianę jasności proporcjonalną do części wspólnej piksela i prostokąta odcinka uzyskamy najprostszy algorytm. Podczas rysowania można wykorzystać bufor cykliczny zawierający pewien wzorzec wypełniania kolejnych punktów odcinka. W ten sposób można uzyskać linie przerywane, kropkowane itd.

 

Na podobnej zasadzie jak rysowanie odcinka, Bresenham opracował algorytm rysowania łuku okręgu (rys.2.6). Oczywiście zmieniają się w tym przypadku warunki wyboru pikseli, ale algorytm ten również wykorzystuje tylko operacje na liczbach całkowitych. Podobnie jak w algorytmie rysowania odcinka tak i tutaj algorytm wyboru pikseli realizuje rysowanie fragmentu łuku (1/8). Pozostałe fragmenty uzyskuje się przez zamianę współrzędnych lub zmianę znaku. Szczegóły algorytmu można znaleźć w książkach [1, 2].

 

Rys.2.6. Rysowanie łuku okręgu na mapie pikseli.

Przy okazji rysowania okręgu warto zwrócić uwagę na parametr charakteryzujący proporcje boków rastra pikseli w pionie i w poziomie, czyli aspekt. Jeśli proporcje rozdzielczości dla kart graficznych 1024x768 wynoszą 4:3, natomiast dla rozdzielczości 1280x1024 wynoszą 5:4, to jeśli chcemy wyświetlić takie obrazy na tym samym monitorze, to proporcje trzeba przeliczyć uwzględniając aspekt. Inaczej narysowany okrąg albo w jednym albo w drugim przypadku będzie miał kształt elipsy.


  Poprzedni
Następny