Poprzedni
Następny  

Rozdział 2. PODSTAWOWE OPERACJE RASTROWE

2.2. Wypełnianie obszaru

Wypełnianie obszaru jest drugim po rysowaniu odcinka lub łuku, najczęściej występującym problemem związanym z prymitywami. Zadanie dla szczególnych przypadków (np. dla prostokąta) jest zadaniem trywialnym. Natomiast w ogólnym przypadku algorytm powinien pracować poprawnie dla dowolnego wielokąta (także wklęsłego), również dla wielokątów z „dziurami”.

Rys.2.7. Wypełnianie obszaru. Równoważność problemów a) wypełniania i b) zmiany barwy obszaru.


Analogicznym zadaniem do wypełniania obszaru jest zmiana barwy w danym obszarze. Zadania są równoważne (rys.2.7). W wypełnianiu obszaru brzegiem są piksele o barwie linii ograniczającej obszar, w zmianie barwy brzegiem są piksele o barwie tła. Algorytm rozwiązujący jedno zadanie może posłużyć do rozwiązania drugiego.

Niech na mapie pikseli dana będzie krzywa zamknięta, zdefiniowana w postaci zbioru sąsiadujących ze sobą pikseli o danej barwie. Zadaniem jest wypełnienie tego obszaru, czyli zmiana barwy wewnętrznych pikseli na zadaną barwę wypełnienia. Znane są dwa klasyczne sposoby rozwiązania tego zadania.

  • Wypełnianie przez spójność (nazywane czasem wypełnianiem przez sianie).
  • Wypełnianie przez kontrolę parzystości.

 

Wypełnianie przez spójność zakłada znajomość punktu startowego (tzw. „ziarna”) wewnątrz obszaru. Punkt ten jest wypełniany, a następnie startując z niego wypełniamy punkty sąsiednie (jeśli oczywiście istnieją – jeśli nie są już wypełnione, ani nie są punktami granicznymi obszaru). Jednocześnie punkty sąsiednie stają się wyjściowymi dla wypełniania w następnym kroku. Procedura ta jest powtarzana dopóki można wskazać punkty wyjściowe (niewypełnione) wewnątrz obszaru. Naturalnym opisem takiego postępowania jest procedura rekurencyjna, jednak ze względu na znane wady takiego rozwiązania, stosowana jest prosta eliminacja rekursji.


Warto zwrócić tutaj uwagę na problem sąsiedztwa i konieczność dostosowania do niego kształtu brzegu. Można wyróżnić dwa przypadki. Gdy ruchy po mapie pikseli mogą odbywać się analogicznie do ruchów wieży po szachownicy – wtedy piksel ma 4 sąsiadów – siatka jest czterospójna (rys.2.8a). Gdy dodamy do tego jeszcze ruchy na ukos (odpowiada to kierunkom ruchów hetmana w szachach), to piksel ma 8 sąsiadów – siatka jest ośmiospójna (rys.2.8b). Czytelnik może przeanalizować jak powinien wyglądać rozkład pikseli brzegu dla obu przypadków aby stanowił on figurę zamkniętą z punktu widzenia możliwości ruchu.

 

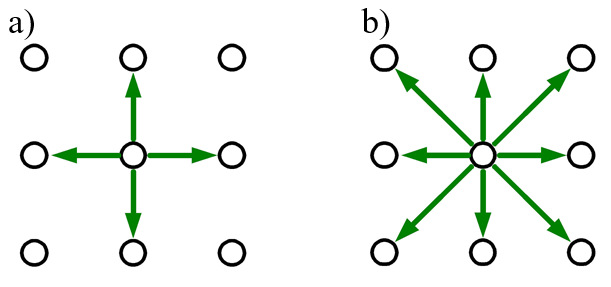
Rys.2.8. Możliwości poruszania się po mapie pikseli. a) siatka czterospójna, b) siatka ośmiospójna.

Algorytm wypełniania przez spójność dla siatki czterospójnej (rys.2.9) wygląda następująco (przyjęto:   c_b – barwa brzegu, c_f – barwa wypełnienia).:

procedure wypełnij1(x,y)
begin
            set_pixel(x,y,c_f);
            if (barwa(x-1,y) inna niż c_b i inna niż c_f) wypełnij1(x-1,y);
            if (barwa(x+1,y) inna niż c_b i inna niż c_f) wypełnij1(x+1,y);
            if (barwa(x,y-1) inna niż c_b i inna niż c_f) wypełnij1(x,y-1);
            if (barwa(x,y+1) inna niż c_b i inna niż c_f) wypełnij1(x,y+1);
end;

Czytelnik może zaproponować korektę algorytmu obejmującą siatkę ośmiospójną.

 

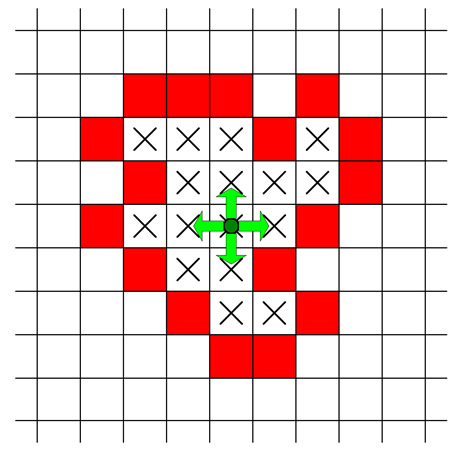
Rys.2.9. Punkt startowy („ziarno”) oraz kierunki wypełniania w pierwszym kroku wypełniania przez spójność.

 

Przedstawiona postać algorytmu wypełniania przez spójność jest algorytmem rekurencyjnym. Daje to łatwość opisu ale związane jest także problemami realizacyjnymi. Z tego powodu znane są wersje niniejszego algorytmu w postaci nierekurencyjnej.


Wypełnianie przez kontrolę parzystości wykorzystuje pewną właściwość przecięcia brzegu linią prostą. Jeśli punkty przecięcia ponumerujemy kolejnymi liczbami naturalnymi zgodnie z orientacją prostej (na rysunku od lewej do prawej dla prostej poziomej) i jeśli będziemy poruszać się po prostej zgodnie z jej orientacją to każde nieparzyste przecięcie będzie „wejściem” do wnętrza obszaru, natomiast każde parzyste będzie „wyjściem” na zewnątrz. Zatem, aby wypełnić obszar należy go przecięć prostymi odpowiadającymi kolejnym rzędom pikseli, a następnie wypełnić odcinkami pomiędzy każdym nieparzystym przecięciem, a najbliższym parzystym (rys. 2.10).

Rys.2.10. Wypełnianie przez kontrolę parzystości.
Odcinki pomiędzy nieparzystym a parzystym punktem przecięcia z figurą są w jej wnętrzu.


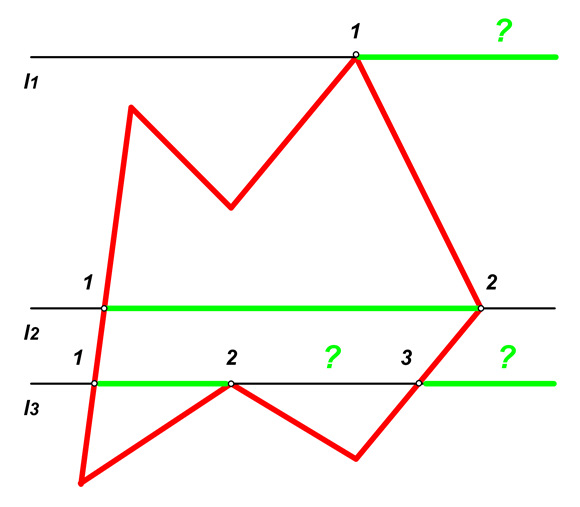
Oczywiście należy zmodyfikować to postępowanie dla przypadków szczególnych, gdy punkt przecięcia jest jednocześnie lokalnym ekstremum brzegu, co zaburza prostą regułę parzystości. Lokalizacja lokalnego ekstremum możliwa jest na podstawie położenia końców przecinanych odcinków. Jeśli są po tej samej stronie prostej wypełniającej – przecinany punkt jest lokalnym ekstremum i nie należy jego liczyć przy analizie parzystości.

Rys.2.11. Problemy brzegowe wypełniania przez kontrolę parzystości.


Na rysunku 2.11 prosta l2 przecina wielokąt w wierzchołku (punkt 2) ale jest to przecięcie zwykłe – pozostałe końce przecinanych boków są po przeciwległych stronach prostej l2.  Prosta l3 również przecina wielokąt w wierzchołku (punkt 2) ale jest to ekstremum lokalne – pozostałe końce boków są po tej samej stronie prostej l3. 

W szczególnych przypadkach mogą pojawić się obszary nie dające się wypełnić w sposób spójny – problem „drzazgi” (rys. 2.12). Jedynym sposobem rozwiązania tego problemu jest nadpróbkowanie. Należy spróbkować i wypełnić drzazgę z większą rozdzielczością, a następnie uśrednić barwę/luminancję wracając do rozdzielczości rastra.

 

Rys.2.12. Problem drzazgi. Taki obszar jest trudny do wypełnienia zarówno algorytmem
wypełniania przez spójność jak i przez kontrolę parzystości.

W książkach [1, 2] można znaleźć szczegółowe opisy oraz pseudokody dla rozwiązania różnych problemów rysowania prymitywów w technice rastrowej.



  Poprzedni
Następny