Podręcznik Grafika komputerowa i wizualizacja

Drugim bardzo prostym zagadnieniem, które często występuje w zagadnieniach graficznych jest określenie zorientowania trójki punktów na płaszczyźnie (rys.3.4). Dane są trzy punkty na płaszczyźnie, należy określić ich zorientowanie. Oczywiście należy pamiętać o przypadkach szczególnych, stąd rozpatruje się punkty różne i niewspółliniowe. Zadanie to ma oczywiście eleganckie rozwiązanie w postaci wektorowej. Wystarczy wyznaczyć dwa wektory rozpięte na badanych trzech punktach, a następnie obliczyć ich iloczyn wektorowy. Analiza zwrotu wektora wynikowego pozwala określić poszukiwane zorientowanie.

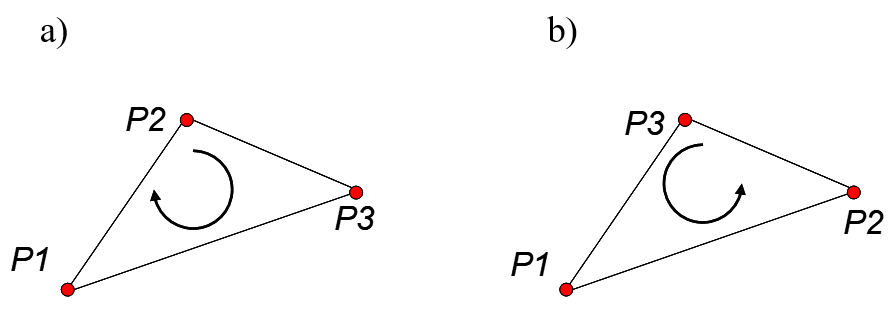
Rys.3.4. Zorientowanie punktów a) zgodnie z ruchem wskazówek zegara,  b) przeciwne do ruchu wskazówek zegara.

Zastosowanie macierzy współrzędnych (przez analogię do macierzy określającej iloczyn wektorowy) upraszcza obliczenia.

Niech dane będą trzy niewspółliniowe punkty P₁[x₁,y₁], P₂[x₂,y₂], P₃[x₃,y₃]. Zadaniem jest określenie zorientowania (rys.3.4).

Można wyznaczyć macierz M :

Analiza wyznacznika tej macierzy pozwala w prosty sposób rozwiązać zadanie.

• Jeśli  det  M > 0    mówimy  o  dodatnim  zorientowaniu  (lewoskrętnym  lub  przeciwnym  do  ruchu  wskazówek  zegara  (CCW – counter-clockwise).
• Jeśli  det  M < 0    mówimy  o  ujemnym  zorientowaniu  (prawoskrętnym  lub  zgodnym  z  ruchem  wskazówek  zegara     (CW – clockwise).