Podręcznik Grafika komputerowa i wizualizacja
Rozdział 3. ELEMENTY GEOMETRII OBLICZENIOWEJ
3.5. Sprawdzenie przynależności punktu do wielokąta
Dość często spotykanym zadaniem geometrycznym
jest sprawdzenie położenia badanego punktu względem określonych obiektów. Może
to obejmować badanie przynależności do określonego obszaru lub lokalizację
położenia na mapie. Najprostszym zadaniem tego typu jest określenie czy badany
punkt znajduje się wewnątrz lub na zewnątrz danego wielokąta.
Badanie przynależności punktu do wielokąta wypukłego
Zagadnienie sprawdzenia przynależności punktu do wnętrza wielokąta ma bardzo proste rozwiązanie dla wielokąta wypukłego. Jeśli wziąć pod uwagę prostą wyznaczoną przez dwa kolejne wierzchołki wielokąta, to prosta ta dzieli płaszczyznę na dwie półpłaszczyzny, z których tylko jedna zawiera wielokąt (rys.3.5). Podstawiając więc współrzędne badanego punktu do równania prostej można na podstawie znaku równania stwierdzić po której stronie prostej punkt się znajduje. A zatem punkt P1 na rysunku będzie po tej samej stronie prostej wyznaczonej przez V1 V2 co np. wierzchołek V4. Natomiast punkty P2 i V4 będą po przeciwnych stronach tej prostej.

Rys.3.5.
Przynależność punktu do wielokąta wypukłego określona na podstawie prostej
wyznaczonej przez kolejne dwa wierzchołki.
Algorytm sprawdzania przynależności punktu do wnętrza wielokąta wypukłego jest następujący.
ALGORYTM PRZYNALEŻNOŚCI 1
Obejdź wielokąt zgodnie z porządkiem kolejnych jego wierzchołków ;
W każdym kroku wyznacz prostą przechodzącą przez bieżący i następny wierzchołek ;
Sprawdź czy badany punkt jest po tej samej stronie prostej co jeden z wierzchołków wielokąta; jeśli w którymkolwiek kroku badany punkt nie spełnia tego warunku, przerwij sprawdzanie – punkt jest na zewnątrz ;
Jeśli po obejściu całego wielokąta okaże się, że punkt był zawsze (!) po tej samej stronie co reszta wielokąta to punkt jest wewnątrz ;
Opisany algorytm należy, w zależności od potrzeb, uzupełnić o analizę samego wielokąta – przynależność lub nie do odpowiednich odcinków brzegu, co jest zabiegiem prostym technicznie i nie stanowi problemu.
Algorytm ten jest łatwy w implementacji i szybki. Jednak jego podstawową wadą jest fakt, że działa poprawnie tylko dla wielokątów wypukłych. Dla wielokątów wklęsłych proste wyznaczone przez kolejne wierzchołki mogą przecinać wielokąt. A w takiej sytuacji założenie, że tylko jedna półpłaszczyzna będzie zawierała elementy wielokąta nie jest prawdziwe.
Dla wielokątów dowolnych problem można rozwiązać algorytmem kontroli parzystości lub algorytmem analizy sumy kątów zorientowanych.
Warto przy tym zwrócić uwagę, że rozpatrywane są tylko wielokąty zwykłe, to znaczy takie, których krawędzie nie mają punktów wspólnych poza wierzchołkami.
Przez analogię do wypełniania wielokąta przez kontrolę parzystości na rastrze pikseli można zaproponować algorytm sprawdzania przynależności punktu do wielokąta.
ALGORYTM PRZYNALEŻNOŚCI 2
Z badanego punktu poprowadź półprostą (w dowolnym kierunku – z punktu widzenia kierunków układu współrzędnych wygodna będzie np. półprosta pozioma) ;
Półprosta ta może przeciąć wielokąt, sprawdź liczbę przecięć:
- jeśli liczba przecięć z bokami
wielokąta jest nieparzysta to punkt leży wewnątrz wielokąta (np.
punkt P1 na rysunku 3.6);
-
jeśli liczba przecięć jest parzysta,
to punkt jest na zewnątrz (np. punkt P2 na rysunku 3.6) ;
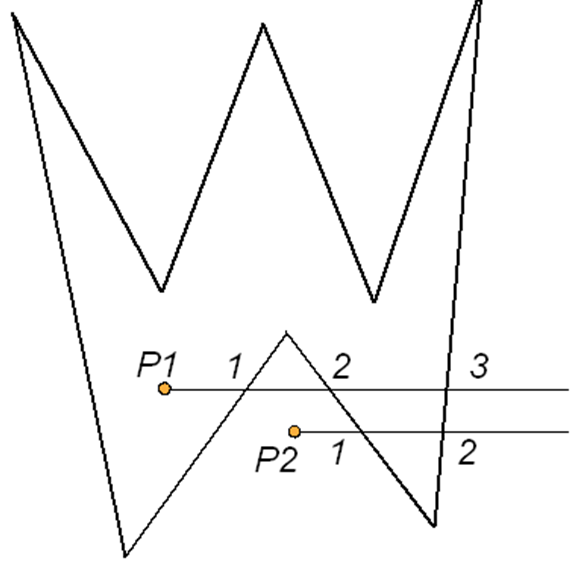
Rys.3.6. Sprawdzenie przynależność punktu do wielokąta wypukłego na podstawie kontroli parzystości przecięć.
Algorytm jest bardzo prosty, jednak pamiętając o
problemach ze szczególnymi przypadkami w algorytmie wypełniania przez kontrolę
parzystości, należy przypuszczać, że podobne sytuacje wystąpią i tutaj.
Oczywiście rozwiązanie jest również analogiczne . Do algorytmu należy dodać dwa
warunki.
- Jeśli punkt przecięcia jest ekstremum lokalnym, to liczymy go podwójnie.
- Jeśli półprosta zawiera cały bok wielokąta, to traktujemy to jako jeden pseudowierzchołek.
Drugim rozwiązaniem problemu sprawdzenia przynależności punktu do wielokąta jest analiza kątów zorientowanych (rys.3.7).

Rys.3.7.
Sprawdzenie przynależność punktu do wielokąta wypukłego
na podstawie sumy kątów zorientowanych. a) suma kątów = 0o , b) suma kątów = 360o.
Można założyć, że wierzchołki wielokąta są uporządkowane przeciwnie do ruchu wskazówek zegara. Z badanego punktu przez każdy wierzchołek wielokąta prowadzimy półprostą. Badany punkt oraz półproste przechodzące przez kolejne wierzchołki wyznaczają kąt, któremu można przypisać zorientowanie analogicznie jak zorientowanie wielokąta (+ jeśli kolejność ramion kąta jest przeciwna do ruchu wskazówek zegara, i – w sytuacji odwrotnej). Po przyjęciu takich założeń wystarczy zsumować wszystkie kąty związane z punktem badanym. Jeśli suma = 360o to punkt jest wewnątrz wielokąta. Jeśli suma = 0o to na zewnątrz.
Oczywiście należy pamiętać o błędach zaokrąglenia i oczekiwanie np. dokładnie zerowej wartości byłoby nieporozumieniem. Jeśli jesteśmy pewni, że w implementacji nie ma błędu, to warunki można postawić jako: suma > 180o i suma < 180o.
