Poprzedni
Następny  

Rozdział 3. ELEMENTY GEOMETRII OBLICZENIOWEJ

3.6. Otoczka wypukła (wypukła skorupka)

Niech S będzie zbiorem n punktów na płaszczyźnie (rys.3.8). Problem otoczki wypukłej (Convex Hull  - CH(S)) polega na wyznaczeniu wielokąta który:

  • zawiera wszystkie punkty S (tzn. punkty są wewnątrz wielokąta lub na jego brzegu),
  • jest wypukły,
  • jest najmniejszy z możliwych.

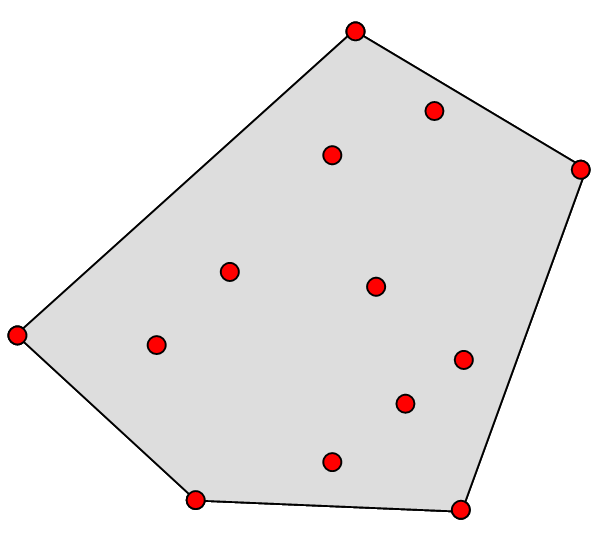
Rys.3.8. Otoczka wypukła


Analizując problem (CH(S)) można zauważyć że:

 

SPOSTRZEŻENIE_1

Jeśli punkty tworzące (CH(S)) nazwiemy punktami skrajnymi, to można zadanie wyznaczenia (CH(S)) podzielić na dwa etapy.

  1. W pierwszym należy wyznaczyć zbiór punktów skrajnych.
  2. W drugim należy posortować zbiór punktów skrajnych pod względem rosnącego kąta   w biegunowym układzie współrzędnych, którego początek znajduje się   wewnątrz (CH(S)).

 

SPOSTRZEŻENIE_2

Aby wskazać punkt, który znajduje się wewnątrz zbioru punktów, wystarczy wyznaczyć współrzędne jako średnie arytmetyczne ze współrzędnych punktów tego zbioru.

 

SPOSTRZEŻENIE_3

Aby wskazać jeden (dowolny) punkt skrajny wystarczy wybrać punkt o ekstremalnej (maksymalnej lub minimalnej) współrzędnej, jeśli jest takich punktów kilka, to spośród nich wybrać ten, którego druga współrzędna jest ekstremalna.

 

SPOSTRZEŻENIE_4

Punkt skrajny nie należy do wnętrza żadnego trójkąta, którego wierzchołkami są punkty ze zbioru.

 

SPOSTRZEŻENIE_5

Aby posortować zbiór punktów skrajnych wystarczy wskazać punkt wewnątrz (CH(S)), umieścić w nim początek biegunowego układu współrzędnych. Biorąc pod uwagę współrzędne punktów skrajnych w układzie biegunowym posortować te punkty pod względem rosnącego kąta.

 

Wykorzystując powyższe spostrzeżenia można zaproponować najprostszy algorytm wyznaczenia (CH(S)):

ALGORYTM CH_1
  1. for every trójka punktów P1,P2,P3 z S do
  2.              for every punkt q z  S do
  3.                         if q leży wewnątrz trójkąta (P1,P2,P3) then    usunąć q z S ;
 

Algorytm ten jest bardzo prosty i łatwy w realizacji. Można byłoby nawet powiedzieć, że jest dość elegancki. Ma jednak jedną, dyskwalifikującą go wadę: wysoką złożoność obliczeniowa. Jeśli zbiór S liczy n punktów, to liczba wszystkich trójkątów o wierzchołkach ze zbioru S jest rzędu n3 (dokładnie ).  A zatem liczba operacji rozpoczętych w kroku 1. jest rzędu n3. W kroku 2. dla każdego trójkąta  brany jest pod uwagę każdy punkt ze zbioru, czyli liczba operacji rośnie n razy. A zatem asymptotyczna złożoność obliczeniowa algorytmu CH_1 wynosi O(n4).

 Spośród wielu znanych algorytmów – efektywnie rozwiązujących problem wypukłej otoczki warto przytoczyć dwa: algorytm Grahama i algorytm Jarvisa.

 

Algorytm Grahama wyznaczania wypukłej otoczki 

Rys.3.9. Wypukła otoczka wyznaczana algorytmem Grahama. Stan po przejrzeniu
7 kolejnych punktów (łącznie ze startowym).  Dwa spośród nich zostały już wyeliminowane.
Czytelnik może przeanalizować  następne dwa kroki przeglądania:
położenie kolejnego punktu  powoduje, że nie tylko ostatni ale i przedostatni punkt
dołączony do tymczasowej wypukłej skorupki zostanie wyeliminowany.


ALGORYTM CH_2 (Grahama)
  1. umieść początek układu biegunowego wewnątrz CH(S) ;
  2. posortuj punkty S względem kąta i odległości  (leksykograficznie)  (dla punktów o tym samym kącie o kolejności decyduje odległość);
  3. wskaż punkt startowy VSTART , który na pewno należy do CH(S) (zgodnie ze   SPOSTRZEŻENIEM 3. wybieramy punkt najniżej i na lewo) ;
  4. startując od VSTART  „przejrzyj” punkty zgodnie z ich posortowaną kolejnością:
    •  jeśli przyjmiemy, że w tym kroku tworząc wypukłą otoczkę obejdziemy zbiór punktów przeciwnie do ruchu wskazówek zegara (CCW), to gdyby trzy kolejne punkty tworzyły CH(S), to będą one miały zorientowanie CCW. Jeśli tak nie będzie, to na pewno środkowy punkt nie należy do CH(S); a zatem:
    •  operując na stosie reprezentującym CH weź pod uwagę zorientowanie ostatnich 2 punktów stosu i punktu bieżącego
      •  jeśli zorientowanie jest  CCW dodaj bieżący do stosu ;
      • jeśli nie CCW, to zdejmij ostatni punkt ze stosu ;

 

Można zastanowić się nad złożonością obliczeniową algorytmu Grahama przyjmując, że w zbiorze S jest n punktów. O złożoności całego algorytmu będą decydowały kroki 2. i 4. algorytmu. Złożoność sortowania (operacja 2.) nie podlega dyskusji i wynosi O(nlogn). Wątpliwości mogłaby budzić operacja 4. Wydawać by się mogło, że jest to wielokrotne cofanie i przeglądanie punktów – branie czasem wielokrotnie tego samego jako bieżącego. Proszę jednak zwrócić uwagę na fakt, że każde takie cofanie w punkcie 4. jest związane z eliminacją dokładnie jednego punktu ze stosu. A to oznacza, że takich „wielokrotnych” cofań mogłoby być co najwyżej n. A zatem krok 4. algorytmu ma złożoność liniową ! Oznacza to, że złożoność całego algorytmu CH_2 (Grahama) wynosi O(nlogn).


Algorytm Jarvisa wyznaczania wypukłej otoczki (marsz Jarvisa)
Algorytm Jarvisa opiera się na dość zaskakującym spostrzeżeniu: w specyficznych warunkach rozwiązanie zadania wyznaczenia wypukłej otoczki jest banalnie proste. Czytelnik zechce zastanowić się jak rozwiązać problem CH(S) mając do dyspozycji: tablicę, młotek, gwoździe, sznurek (rys.3.10).

Rys.3.10. Jak wyznaczyć wypukłą otoczkę mając do dyspozycji tablicę, młotek, gwoździe i sznurek.
Algorytm Jarvisa jest czasem nazywany „algorytmem owijania prezentu”.


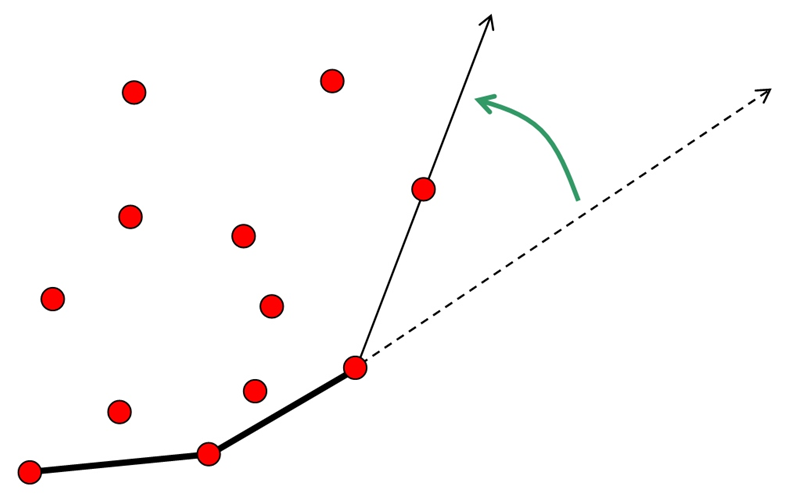
Przełożenie tej prostej idei na formalny język algorytmów geometrycznych nie jest zabiegiem trudnym jeśli zauważymy, że „owinięcie” można zrealizować jako wybór odpowiedniego punktu na podstawie jego położenia (kąta !) w odpowiednim układzie współrzędnych biegunowych (rys.3.11). Jest to wybór takiego punktu, który definiuje nową półprostą tworzącą najmniejszy kąt z dotychczasową półprostą związaną z „owijaniem".

Rys.3.11. Dołączanie kolejnego punktu do wypukłej otoczki w algorytmie Jarvisa



ALGORYTM CH_3 (marsz Jarvisa)
  1. wyznacz punkt startowy należący do CH(S)   (- położony najniżej i najbardziej na lewo) ;   punkt startowy staje się punktem bieżącym algorytmu; dodaj go do wypukłej otoczki;   zdefiniuj półprostą dotychczasową jako półprostą wychodzącą z punktu   startowego poziomo w prawo ;
  2. w punkcie bieżącym umieść początek układu biegunowego ;    „owiń prostą” biorąc pod uwagę kąty do kolejnych punktów zbioru    w tym celu wybierz punkt, który definiuje półprostą tworzącą najmniejszy kąt   z dotychczasową półprostą ;      punkt ten staje się punktem bieżącym; dodaj go do wypukłej otoczki ;      zdefiniowana przez ten punkt półprosta staje się półprostą dotychczasową ;
  3. powtórz krok 2. dla  kolejnego punktu aż do dotarcia do punktu startowego;

Niech w zbiorze S jest n punktów. O złożoności całego algorytmu będzie decydowała liczba powtórzeń kroku 2. oraz złożoność operacji w tym kroku. Wybór punktu związanego z najmniejszym kątem nie wymaga sortowania, ale wymaga sprawdzenia kątów wszystkich punktów. Zatem jednorazowe wykonanie kroku 2. algorytmu wymaga wykonania n operacji. Z drugiej strony krok ten będzie powtarzany tyle razy ile wynosi liczba punktów wypukłej otoczki. Jeśli przyjmiemy, że jest to k , to złożoność całego algorytmu wyniesie O(nk) .

Jest to ciekawy przypadek algorytmu, którego złożoność zależy od wprowadzonych danych (położenia punktów). Gdyby k i n były porównywalne (w skrajnym przypadku równe czyli wszystkie punkty zbioru tworzą CH(S)), to algorytm miałby złożoność bliską kwadratowej i byłby gorszy pod tym względem od algorytmu Grahama. Jeśli jednak k<<n  (co w praktyce często się zdarza) to algorytm Jarvisa byłby bardzo efektywny.

Więcej na temat wypukłej otoczki i algorytmów z nią związanych (np. łączenia dwóch otoczek) można znaleźć w książkach [2,4,9]. Problem ten rozpatruje się także w trzech wymiarach. Algorytmy wyznaczania wypukłej skorupki w 3D są opisane między innymi w [3, 5, 8].



  Poprzedni
Następny