Podręcznik Grafika komputerowa i wizualizacja
Rozdział 4. PRZEKSZTAŁCENIA GEOMETRYCZNE
4.1. Współrzędne jednorodne znormalizowane
Współczesna grafika komputerowa operując na milionach elementów (punktów, trójkątów) wymaga opisu operacji geometrycznych w taki sposób, aby ich wykonanie było z jednej strony efektywne, a z drugiej, aby opis był prosty i ujednolicony. Zastosowanie opisu macierzowego pozwala spełnić te założenia. Wymaga to jednak zmiany tradycyjnego opisu położenia na opis we współrzędnych jednorodnych.
Można zastanowić się nad tym, dlaczego stosowana są współrzędne jednorodne, czy nie można analogicznych operacji opisać po prostu we współrzędnych punktu.
Rozpatrzmy zestaw przekształceń na płaszczyźnie: obrót, skalowanie, przesunięcie (translację). Można zaproponować macierz 2x2, która, opisuje obrót punktu wokół początku układu współrzędnych. Analogiczny opis można zaproponować dla operacji skalowania.
Niech ![]() opisuje położenie punktu na płaszczyźnie.
opisuje położenie punktu na płaszczyźnie.
Niech macierz 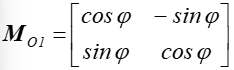 opisuje obrót punktu
wokół początku układu współrzędnych (rys 4.1 a).
opisuje obrót punktu
wokół początku układu współrzędnych (rys 4.1 a).
![]() czyli
czyli  i jest to zgodne z oczekiwaniami.
i jest to zgodne z oczekiwaniami.
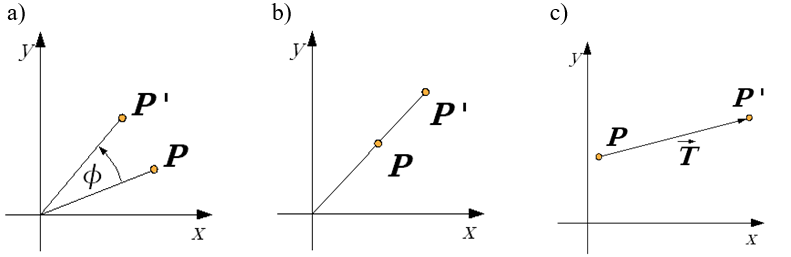
Rys.4.1.
a) Obrót punktu na płaszczyźnie wokół początku układu współrzędnych.
b)
Skalowanie względem początku układu współrzędnych. c)
Przesunięcie o wektor.
Analogicznie można opisać operację skalowania.
Macierz ![]() opisuje skalowanie
względem początku układu współrzędnych (rys 4.1 b).
opisuje skalowanie
względem początku układu współrzędnych (rys 4.1 b).
![]() czyli
czyli 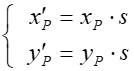
Ale czy można tak opisać translację (przesunięcie) – rysunek 4.1c) ???
Niech ![]() . Niech wektor
. Niech wektor ![]() opisuje translację
punktu na płaszczyźnie.
opisuje translację
punktu na płaszczyźnie.
Czy można znaleźć takie ![]() , aby
, aby 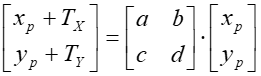 dla
dla ![]() i
i ![]() .
.
Widać że nie jest to możliwe dla współrzędnych
dowolnego punktu. Punkt ![]() byłby punktem stałym
takiego przekształcenia.
byłby punktem stałym
takiego przekształcenia.
Niech xp, yp, zp,
opisują położenie punktu w 3D kartezjańskim układzie współrzędnych. W grafice
komputerowej do opisu położenia oraz opisu operacji (transformacji
geometrycznych), którym punkty będą podlegały, jest używany układ współrzędnych jednorodnych
znormalizowanych. Dzięki temu wszystkie stosowane transformacje
geometryczne mogą być opisane w identyczny sposób za pomocą mnożenia
macierzowego. Jeśli współrzędne xp,
yp, zp opisują położenie punktu to odpowiada temu wektor ![]() we współrzędnych
jednorodnych znormalizowanych. We współrzędnych nieznormalizowanych wektor ten
miałby postać
we współrzędnych
jednorodnych znormalizowanych. We współrzędnych nieznormalizowanych wektor ten
miałby postać ![]() dla
dla ![]() , ale takich reprezentacji mogłoby być nieskończenie wiele.
Problem takiej niejednoznaczności rozwiązuje operacja normalizacji:
, ale takich reprezentacji mogłoby być nieskończenie wiele.
Problem takiej niejednoznaczności rozwiązuje operacja normalizacji: 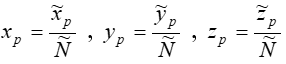 .
.
Wszystkie opisy położenia w niniejszym podręczniku będą się odnosić do współrzędnych jednorodnych znormalizowanych.
Niech zatem położenie punktu o współrzędnych (xp, yp, zp) reprezentuje wektor P :
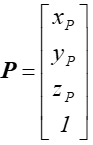
Jeśli
macierz ![]() opisuje pewną
transformację geometryczną to operację tę można opisać następująco:
opisuje pewną
transformację geometryczną to operację tę można opisać następująco:
![]()
czyli:
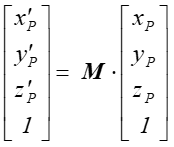
gdzie ![]() opisuje położenie punktu po przekształceniu. Oczywiście jeśli
wynik mnożenia macierzy jest nieznormalizowany, to należy dokonać normalizacji.
opisuje położenie punktu po przekształceniu. Oczywiście jeśli
wynik mnożenia macierzy jest nieznormalizowany, to należy dokonać normalizacji.
Zastosowanie
w tym przypadku współrzędnych jednorodnych można sobie wyobrazić jako
umieszczenie płaszczyzny, na której pracujemy, w trójwymiarowym układzie
współrzędnych, w taki sposób, aby nie przechodziła ona przez początek układu
(tzn. dla ![]() ). Wtedy analogiczne opisanie operacji translacji na
płaszczyźnie (ale już jako macierz 3x3) da poprawne rozwiązanie, gdyż punkt
stały – początek układu współrzędnych jest poza płaszczyzną, na której jest
wykonywana operacja. Jednocześnie, aby wynik operacji znajdował się na tej
samej płaszczyźnie, najprościej operować na współrzędnych znormalizowanych,
czyli pracować na płaszczyźnie
). Wtedy analogiczne opisanie operacji translacji na
płaszczyźnie (ale już jako macierz 3x3) da poprawne rozwiązanie, gdyż punkt
stały – początek układu współrzędnych jest poza płaszczyzną, na której jest
wykonywana operacja. Jednocześnie, aby wynik operacji znajdował się na tej
samej płaszczyźnie, najprościej operować na współrzędnych znormalizowanych,
czyli pracować na płaszczyźnie ![]() . Analogicznie dla przekształceń trójwymiarowych można
wyobrazić sobie umieszczenie przestrzeni 3D i trójwymiarowego układu
współrzędnych wewnątrz układu czterowymiarowego, tak aby nie zawierał on
początku układu współrzędnych.
. Analogicznie dla przekształceń trójwymiarowych można
wyobrazić sobie umieszczenie przestrzeni 3D i trójwymiarowego układu
współrzędnych wewnątrz układu czterowymiarowego, tak aby nie zawierał on
początku układu współrzędnych.
W grafice komputerowej operacje na płaszczyźnie opisuje macierz 3x3 w układzie 3D, natomiast operacje w przestrzeni 3D opisuje macierz 4x4 w przestrzeni 4D. Oczywiście w układach znormalizowanych.
Można
powiedzieć, że macierz ![]() definiuje liniowe
funkcje określające każdą ze współrzędnych punktu tzn.:
definiuje liniowe
funkcje określające każdą ze współrzędnych punktu tzn.:

Wykorzystując rachunek macierzowy przekształcenia punktu można opisać również za pomocą prawostronnego mnożenia macierzy. Wtedy, dla przyjętych wyżej danych operacja wyglądałaby tak.
![]()
Jak widać tę samą operację można zapisać jako mnożenie lewostronne lub prawostronne przez macierz przekształcenia.
Tak naprawdę trudno byłoby wskazać uzasadnienie dla wyboru jednej lub drugiej formy zapisu. W książkach dotyczących grafiki komputerowej w ostatnich latach częściej stosowany jest zapis lewostronnego mnożenia, chociaż są autorzy, którzy nadal konsekwentnie trzymają się mnożenia prawostronnego. Natomiast sposób używania zależy od przyzwyczajeń i upodobań użytkownika. Jedno jest jednak bardzo istotne – konsekwencja. Nie można mieszać postaci opisu.